BFS 미로

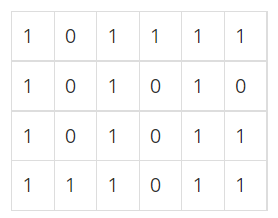
n x m크기의 배열로 표현된 미로가 있다.
0인 칸은 이동할 수 없고 1인 칸만 이동할 수 있다.
(1,1)에서 (n,m)까지 가는 최단 거리를 구해보자.

https://www.youtube.com/watch?v=dzgmLJaTlBo
이 문제는 BFS를 이용해 해결할 수 있다.
(1,1)에서 갈수 있는 상하좌우로 한칸씩 이동하면 카운팅한다.
0을 만나거나, 범위를 벗어나거나, 한번 밟은 칸은 다시 갈 수 없다.
갈 수 있는 모든 경로로 이동하다가 가장 먼저 (n,m)에 도착하면 그 경로의 카운트를 리턴한다.
즉 BFS를 사용하면 목적지를 찾자마자 최단 경로가 보장된다.

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main 
{
	static int[][] maze = new int[101][101]; // 미로 배열
	static int[][] visited = new int[101][101]; // 방문 처리
	static int n; // y
	static int m; // x
	public static boolean check(int y, int x)
	{ // 이동가능한 블록인지 판단
		// 1일때만 이동 가능
		if (maze[y][x] != 1) return false;
        
		// 상하좌우 범위 넘으면 안됨
		if (y < 1 || y > n || x < 1 || x > m) return false;
        
		// 한번 방문한곳은 다시 안감
		if (visited[y][x] == 1) return false;
		return true;
	}
	
	public static void main(String[] args)
	{
		Scanner sc = new Scanner(System.in);
		n = sc.nextInt(); // y
		m = sc.nextInt(); // x
		/*for (int i=1; i<=n; i++)
		{
			for (int j=1; j<=m; j++)
			{
				maze[i][j] = sc.nextInt();
			}
		}*/
		
		// 숫자 다 붙어있어서 문자열 n개를 받고 charAt으로 쪼개자.
		for (int i=1; i<=n; i++) // 4
		{
			String ans = sc.next();
			for (int j=1; j<=m; j++) // 6
			{
				maze[i][j] = ans.charAt(j-1) - '0'; // 아스키 코드
			}
		}
		
		Queue<Integer> queueY = new LinkedList<>();
		Queue<Integer> queueX = new LinkedList<>();
		Queue<Integer> queueCount = new LinkedList<>();
		
		queueY.add(1);
		queueX.add(1); // 처음 위치 넣기
		queueCount.add(1);
		
		int count = 0;
		
		while (!queueX.isEmpty()) // 둘중 하나가 빌때까지
		{
			int currY = queueY.poll();
			int currX = queueX.poll();
			int currCount = queueCount.poll();
			if (visited[currY][currX] == 1) continue;
			visited[currY][currX] = 1;
			
			if (currY == n && currX == m)
			{ // 도착 시
				count = currCount;
				break;
			}
			
			// 상
			if (check(currY - 1, currX))
			{
				queueY.add(currY - 1);
				queueX.add(currX);
				queueCount.add(currCount + 1);
			}
			// 하
			if (check(currY + 1, currX))
			{
				queueY.add(currY + 1);
				queueX.add(currX);
				queueCount.add(currCount + 1);
			}
			// 좌
			if (check(currY, currX - 1))
			{
				queueY.add(currY);
				queueX.add(currX - 1);
				queueCount.add(currCount + 1);
			}
			// 우
			if (check(currY, currX + 1))
			{
				queueY.add(currY);
				queueX.add(currX + 1);
				queueCount.add(currCount + 1);
			}
		}
		
		System.out.println(count);
	}
}