알고리즘

정렬 알고리즘은 크게 크기에 의한 분할 후 정렬과, 특정 값에 의한 분할 후 정렬로 나눌 수 있다.크기에 의한 분할에는 삽입 정렬(insertion), 병합 정렬(merge)이 있다.특정 값에 의한 정렬에는 선택 정렬(selection), 힙 정렬(heap), 빠른 정

삽입정렬 Insertion sort *key!! 삽입 정렬은 정렬된 앞부분과 정렬 안된 뒷부분으로 나뉜다. 정렬 안된 부분의 첫 요소를 정렬된 부분에 끼워 넣는것(삽입)을 반복한다. i번째 반복하기 전에 arr[0 .. i-1]은 정렬되어 있다는 사실을 이용한다. 알

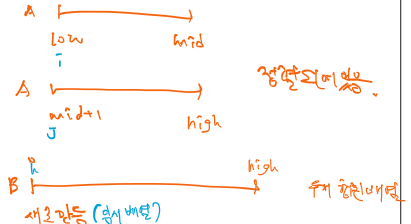
병합정렬은 배열 계속 반으로 나누면서 왼쪽 반, 오른쪽 반 각각 정렬해서 합병하는 알고리즘이다. (분할 후 정복)임시 저장을 위해 다른 배열이 하나 필요하다. 원 배열 A, 임시 배열 B병합 정렬을 Top Down 방식(재귀)을 이용해 구현하면 다음과 같다.Top Do

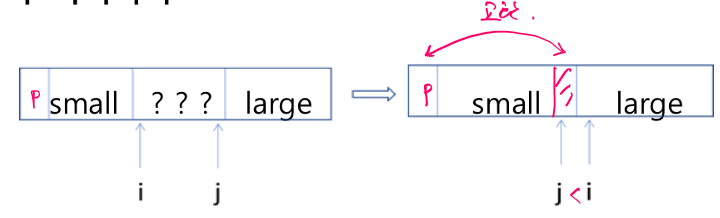
퀵 소트는 가장 빠른 알고리즘은 아니지만 평균적으로 매우 효율적인 알고리즘이다. 기본 아이디어는 배열의 한 원소를 기준으로 (보통 arr0) 작거나 같은 요소는 왼쪽으로, 큰 값은 오른쪽으로 보내고 각각 왼쪽과 오른쪽 배열을 다시 재귀적으로 정렬하는 것이다.가장 첫 원

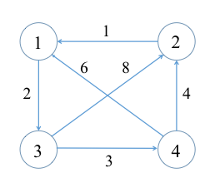
Floyd Warshall 알고리즘 \*거쳐가는 노드!!FW알고리즘은 다익스트라 알고리즘 처럼 최단 거리를 찾는 알고리즘이다. 다익스트라와의 차이라고 한다면 다익스트라는 한 정점에서 다른 모든 정점가지의 최단거리를 구하는데 반해 FW는 모든 정점에서 다른 모든 정점까지

dp를 이용해 구할 수 있다.https://www.youtube.com/watch?v=L27_JpN6Z1Q

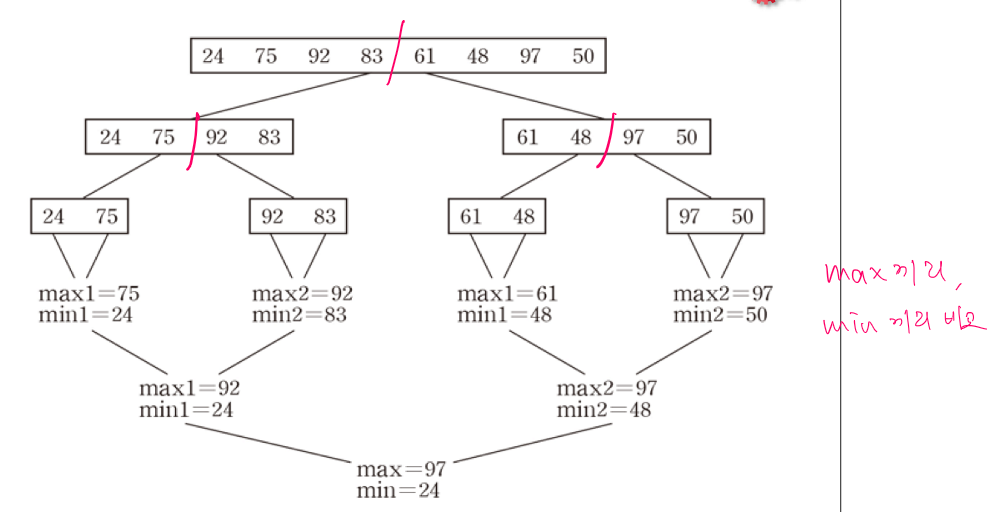
분할 정복을 이용한 최솟값, 최댓값 찾는 알고리즘.배열을 계속 해서 반으로 나누면서 각 배열의 최솟값, 최댓값을 다른 배열과 비교한다.반으로 나누고 최소, 최댓값들을 반복해서 비교하기 때문에 재귀를 사용한다.트리에서 내부 노드들의 합은 리프 노드들보다 하나 작은 n-1

거스름돈 문제와 마찬가지로 동적 할당을 이용해서 해결할 수 있다.인접한 동전 두개를 선택할 수 없기 때문에 예를 들어 6개중 최대값을 내야 한다고 했을때 5개중 최대값 결과, 혹은 4개중 최대값 결과 + 6번째 동전 과 같은 식으로 dp를 이용해 해결할 수 있다.

이진 탐색(Binary Search) start, end mid(인덱스)!! 이진 탐색은 정렬된 배열에서 특정 값 key를 찾는 알고리즘이다. 배열이 오름차순으로 정렬되어 있다고 할 때 key와 중간값을 비교한뒤 작으면 배열의 왼쪽 반에서, 크면 배열 오른쪽 반에서 다

a^n을 계산하려고 할 때 a를 n번 곱하는 식으로 계산하면 O(n)의 시간이 걸린다. 하지만 분할 정복을 이용하면 O(logn)까지 시간을 단축할 수 있다.n이 짝수일때 a^n = (a^n/2)^2n이 짝수일때 a^n = (a^n/2)^2 \* a다음 점화식을 이용하

정수 배열에서 과반보다 많이 존재하는 요소를 찾는 알고리즘이다. 분할 정복을 이용하면 O(n log n)의 시간에 해결할 수 있다. 배열에 과반수 요소가 있다고 가정한다. 있을 지 없을지 모른다고 할때는 반복문을 한번 돌리면서 결과로 나온 숫자가 몇번 나오는지 보면 된

Knapsack Problem최대 용량이 W인 가방에 최대 가치의 물건들을 집어 넣는 문제이다.dp를 이용해 해결할 수 있다.이전에 해결한 부분 문제가 다음 문제를 해결하는 데 도움이 된다.f(i, j)가 1~i번째의 물건을 용량 j인 가방에 넣는다고 할 때1) 최적해

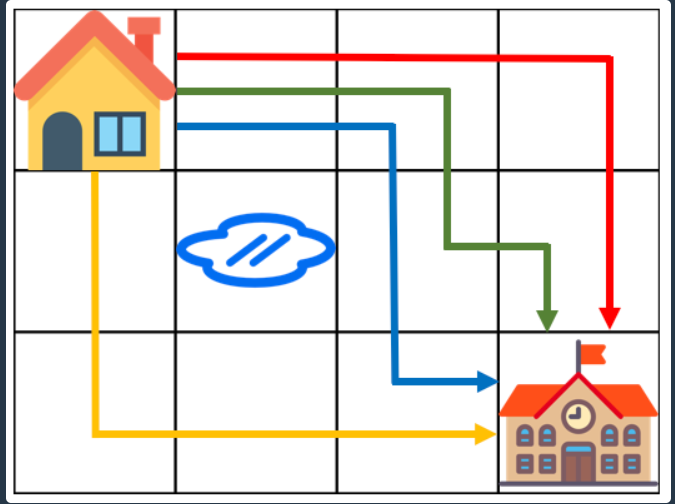
https://programmers.co.kr/learn/courses/30/lessons/42898등굣길 경로의 경우의 수를 구하는 문제이다. 좌표 (1,1)인 집에서 부터 (m,n)인 학교까지 가는 경로를 구하는 문제인데 사이에 웅덩이를 피해 가야한다. p

다음과 같은 피라미드가 있을 때 A에서 맨 밑의 K, L, M, N, O 까지 내려오는 경로를 구하는 문제이다. 각 지점에서 왼쪽 아래 또는 오른쪽 아래로 내려갈 수 있다.이 문제는 dp를 이용해서 해결 할 수 있다. 예를 들어 A에서 L까지 가는 경로는 A에서 G까지

막대 자르기 동적 계획 Dynamic Programming시간 복잡도는 분할 정복일때 O(2^n), 동적 계획일 때 O(n^2).메모이제이션

A팀과 B팀이 총 N경기인 시리즈 결승에 올랐다. N/2+1 경기를 먼저 이기는 팀이 우승을 하게 된다.A가 한 경기를 이길 확률은 p이고 비길 경우는 없다고 가정한다.A가 시리즈을 우승 하기 위해 i 게임을 더 이겨야 하고 B가 우승 하기 위해서는 j 게임 더 이겨야

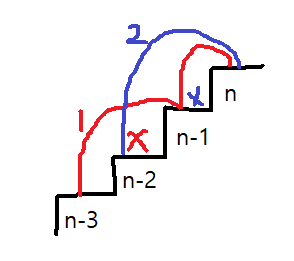
https://www.acmicpc.net/problem/2579각 계단마다 점수가 있고 최대의 점수를 획득하면서 꼭대기 까지 가는 게임이다. 도착 계단은 반드시 밟아야 한다.한번에 한칸 또는 두칸을 갈 수 있고 연속으로 3칸은 갈 수 없다.계단 점수 배열을

https://www.acmicpc.net/problem/1463정수 n이 주어질 때 다음 세 연산을 최소로 사용해 1로 만드는 문제이다.x % 3 == 0이면 3으로 나눔x % 2 == 0이면 2로 나눔1을 뺀다메모이제이션을 사용해 O(n)에 해결할 수 있다

https://www.acmicpc.net/problem/1931한 회의실에 최대한 많은 회의를 배정해야 하는 문제이다. 그리디 알고리즘을 이용하여 해결할 수 있다.각 회의가 시작하는 시간과 끝나는 시간이 입력으로 들어온다.그리디 알고리즘의 기준은 빨리 끝나는

되추적(backtracking)은 완전 탐색을 개선한 기법으로 후보 해들을 만드는 도중 한 후보해가 최종 해가 될 수 없다고 판단되면 멈추고 다른 해를 탐색한다. 상태 공간 트리를 만들고 깊이 우선 탐색을 진행한다. 유망하지 않은 노드는 가지를 쳐서 탐색을 중단한다.이

퀵 소트와 비슷한 방법으로 분할 정복을 이용해 구할 수 있다.시간 복잡도는 최선의 경우(찾는 값이 기준 요소일때) θ(N)이지만, 최악의 경우(퀵 소트와 마찬가지로 정렬되어 있어서 한 그룹은 비어있고, 다른 그룹은 기준 요소 제외한 모든 요소 담겨있을때) θ(N^2)이

Longest Increasing Subsequence최장 증가 부분 수열원소가 n개인 수열에서 최대한 많은 원소를 골라 증가하는 부분 수열을 만드는 문제이다.예를 들어 {10,20,10,30,20,50} 과 같은 수열이 있을 때 {30,50}, {10,30,50},

https://www.youtube.com/watch?v=k5A3HicbLec Binary Search 중복된 데이터가 존재하는 배열을 탐색할 경우 좀 더 응용된 방법을 사용해야 한다. Lower Bound key보다 크거나 같은 첫번째 값 Upper Bound k

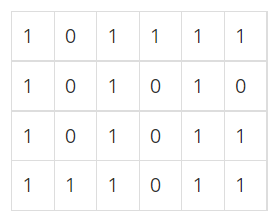
n x m크기의 배열로 표현된 미로가 있다.0인 칸은 이동할 수 없고 1인 칸만 이동할 수 있다.(1,1)에서 (n,m)까지 가는 최단 거리를 구해보자.https://www.youtube.com/watch?v=dzgmLJaTlBo이 문제는 bfs를 이용해 해결

온라인 알고리즘 : Stream처럼 들어오는 데이터 모두 저장하는 것이 아닌 들어오는 대로 바로바로 처리하는 알고리즘. 슬라이딩 위도우도 이 중 하나! 창문으로 보이는 부분 만큼만 저장하는 것. 어디서 들어봤나 생각했는데 운영체제에서 들어본 것이었음. -> 슬라이딩