이진 탐색 트리 (BST)
- 모든 노드의 왼쪽 서브 트리는 해당 노드보다 작은 값을, 모든 노드의 오른쪽 서브 트리는 해당 노드 값보다 큰 값들만을 가진다
- 자식 노드는 최대 두 개
B tree
- 이진 트리를 더 일반화 (노드가 가질 수 있는 키 값 증가)
- 자식 노드의 개수를 결정할 수 있다. 각 노드가 여러 값을 가질 수 있다
- M : 각 노드의 최대 자녀 노드 수, 최대 M개의 자식을 갖는 B tree를 M차 B tree라 함
- M-1 : 각 노드의 최대 key 수
- ⌈M/2⌉ : 각 노드의 최소 자녀 노드 수 (root node, leaf node 제외)
- ⌈M/2⌉-1 : 각 노드의 최소 key 수 (root node, leaf node 제외)
B tree 데이터 삽입
- 추가는 항상 leaf노드에
- 노드가 넘치면 가운데 key를 기준으로 좌우 key들을 분할하고 가운데 key를 올림
B tree 데이터 삭제
- leaf 노드에서 발생
- internal 노드에서는 leaf 노드의 데이터와 위치를 바꾸어 삭제
- 삭제 후 최소 key 수 보다 적어지면 재조정
- key 수가 여유있는 형제의 지원을 받는다
- 1번이 불가능하면 부모의 지원을 받고 형제와 합친다
- 2번 후 부모에 문제가 있다면 거기서 다시 재조정
B tree 특징
- 모든 leaf 노드들이 같은 레벨에 있다.(balanced tree)
DB index로 B tree 계열이 사용되는 이유
- 조회 삽입 삭제의 avg case, worst case 가 항상 O(logN)
- BST의 경우 balanced 하지 않으므로 O(N)이 걸릴 수 있음
self-balancing이면서 똑같이 O(logN)인 AVL이나 Red-Black보다 B tree를 사용하는 이유?
- 컴퓨터 구조 cpu, main memory, secondary storage
- secondary storage의 데이터 처리 속도가 가장 느리고 용량이 가장 크다. 블록 단위로 데이터를 읽고 쓴다
- DB는 secondary strage에 저장되고 필요한 데이터를 RAM에 올려서 처리
- DB에서 데이터 조회시 secondary storage에 최대한 적게 접근하는 것이 좋다
- block 단위로 읽고 쓰므로 연관 데이터를 모아 저장하면 더 효율적으로 읽고 쓸 수 있다.
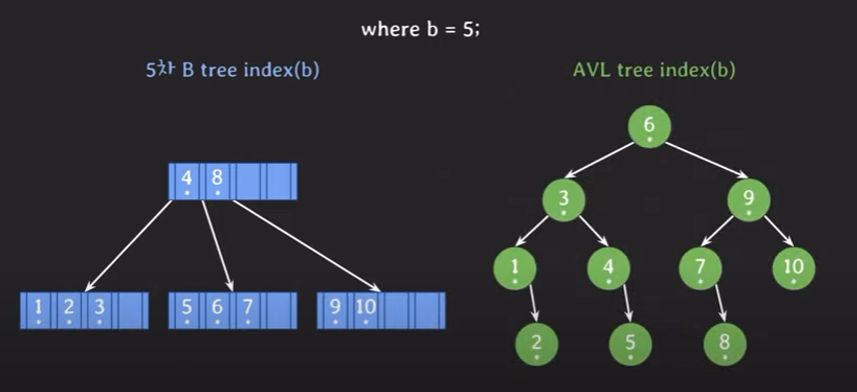
- storage 접근 횟수에 있어 B tree가 성능적으로 우수하다.
- lock 단위에 대한 저장 공간 활용도가 더 좋다
- 보통 한 블록에 하나의 노드가 담기는데, 한 블록을 불러올 때 b tree가 더 많은 키와 포인터를 읽어온다.
- 데이터 검색 시 줄여나가는 탐색 범위가 B tree가 큼 (자식 노드의 수가 더 많으므로)
- hash index는 equality 조회만 가능하고 범위 기반 검색이나 정렬에 사용될 수 없음
공부 기록