우리가 수를 알 수 없는 많은 사람이 기재되어있는 전화번호부에서 특정 한 사람을 찾는다고 가정해보자 만약 규칙없이 뒤섞여 있는 상태라고 한다면 리스트안의 모든 사람들을 비교해나가야 할 것이다.
<규칙없이 뒤섞인 상태에서 김보람찾기>
곽보람, 채보람, 강보람, 문보람, 임보람, 성보람, 전보람, 한보람
만약 리스트가 어떤 규칙에 의해 정렬되어있다면 어떨까 예를 든 이름 리스트가 자음순으로 배열되어있다고 가정하고

"김보람"을 찾아보자 아마도 다음과 같은 순으로 찾아나갈 것이다 말로 풀자면
자음순으로 정렬되어있다고 생각한 순간 김보람을 찾기 위해 리스트의 반절중 뒷부분은 보지 않을 것이다 왜? 기억(ㄱ)은 앞부분에 위치할거라고 확신하기 때문이다. 그렇게 그룹을 반으로 나누고 고려대상에서 제외할 그룹은 무시하고 또 그룹을 나누고 제외할 그룹은 무시되고를 반복하여 결국 결과에 도달할 것 이다(여기서는 "김보람"을 찾았을 것이다)

이 검색 알고리즘을 "이진 검색"이라고 한다. 이진 검색에서 중요한 부분은 일의 양이 데이터의 양이 증가함에 비해 천천히 증가한다는 점이다. 1000개중 1개의 이름을 찾을때는 이름 10개를 확인해야한다. 2000개가 있을 땐 어떨까 두배로 양이 늘었지만 이름은 한개만 더 확인하면된다 11개를 확인하면 된다는 이야기다 왜냐하면 첫 그룹을 나누어 확인하면서 2000의 반절인 1000이 검색대상에서 제외되기 때문이다. 즉 데이터의 양이 1000배 많아지더라도 일은 10번의 단계만을 더 거치게 된다.
앞에서도 이야기했듯 이렇게 찾아 내기 위해서는 "정렬"이 앞선 조건일텐데 이 정렬은 어떻게 할 수 있을까 선택 정렬과 퀵정렬에 대해 알아보자
선택 정렬은 매 회전마다 가장 적합하다고 판단되는 값을 선택해 나가는 방법이다
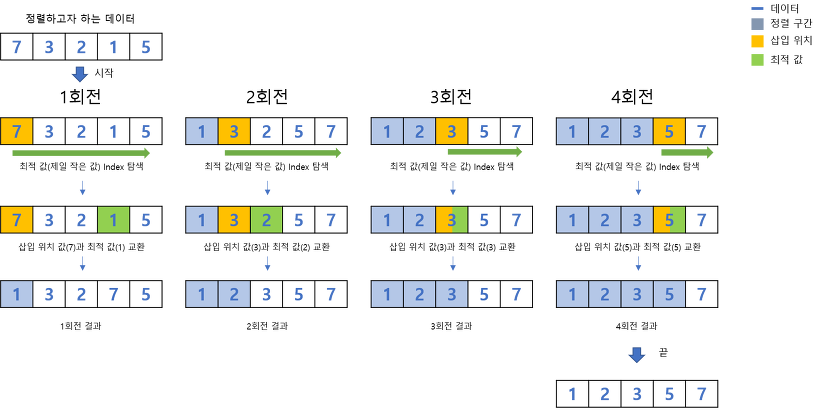
구현이 쉬운편이고 정렬을 위한 비교 횟수가 많지만 실제 교환 횟수는 적기에 많은 교환이 일어나야하는 자료상태에서 효율적 이지만 항상 O(N^2)의 시간복잡도를 갖는 오래 걸리는 정렬 방식이다.
퀵 정렬은 분할 정복방법을 통해 주어진 배열을 정렬하는데 쓰인다 이글의 첫시작인 이진검색에 알맞는 정렬방법이라고 할 수 있다
분할 정복:문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략
배열 가운데 피벗을 고른다(피벗을 고르는 과정에는 아직도 많은 논쟁이 있다)피벗 앞에는 피벗보다 값이 작은 요소가 오고, 피벗 뒤에는 피벗보다 값이 큰 요소가 오도록 피벗을 기준으로 배열을 둘로 나눈다 이렇게 배열을 둘로 나누는 것을 분할(Divide) 이라고 하고 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다. 분할된 배열에 다시 이 과정을 반복하는 것을 반복하며 정렬을 마치는 것이다.
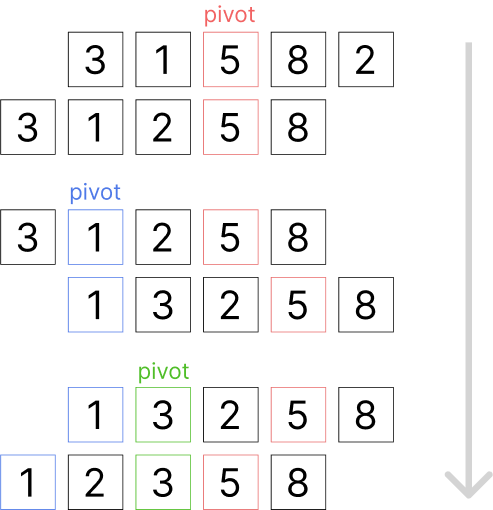
위 그림은 퀵정렬의 개념을 요약한 그림이다 좀 더 디테일한 설명을 원한다면
[알고리즘] 퀵 정렬(quick sort)이란을 참고하자
퀵 정렬은 분할로 이루어진 정렬법으로 분할과정에서 logN의 시간이 걸리게 되고 전체적으로 보면 NlogN의 시간이 걸리게 된다. 이는 다른 정렬방법중 비교적 준수한 속도이다 하지만 선택된 피벗에 따라서 시간복잡도가 매우 크게 다를 수 있다는 단점이 있다 즉 최악의 피벗을 고른다면 O(N^2)의 시간복잡도를 가질 수 도 있다
