[Algorithm] AC-3 Algorithm

시험 공부하다가 정리하는 글입니다.

AC-3은 Arc-Consistency 3의 약어로, 제약 충족 문제 Constraint satisfaction problem (CSP)에서 사용되는 알고리즘입니다. CSP는 변수의 집합, 각 변수의 도메인, 제약 조건의 집합으로 정의 되는 문제의 유형입니다. CSP에서 목표는 각 변수에 대한 값을 찾아내서 모든 constraints를 만족시키는 것입니다.

AC-3 알고리즘의 작동 순서는 다음과 같습니다.

1. Turn each binary constraint into two arcs (e.g., A!=B becomes B!=A)
2. Add all the arcs to an agenda
3. Repeat until agenda is empty

• Take an arc$(x_i, x_j)$ off the agenda and check it
• For every value of $x_i$, there must be some values of $x_i$
• Remove any inconsistent value from $x_i$
• If $x_i$ has changed, add all arces of the form $(x_j,x_i)$ to the agenda.

4. We have an arc constraint problem. It is easier to be solved.

글로 보면 좀 설명이 불편하고 예시를 통해 살펴보겠습니다.

$A$ = {1, 2, 3}, $B$ = {1, 2, 3}, $C$ = {1, 2, 3}가 주어졌을 때, 제약조건은 $A>B$, $B=C$를 만족하도록 변수의 도메인을 결정지어 봅시다.

1. Turn each binary constraint into two arcs.
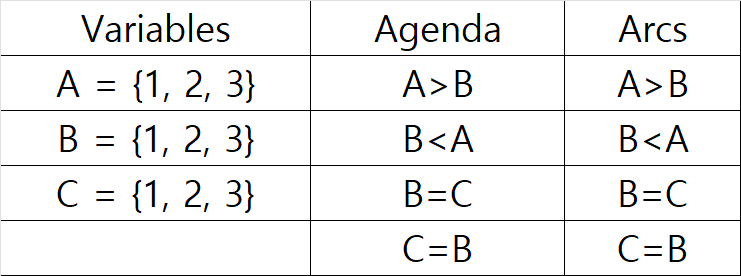
   제약조건은 $A>B$, $B=C$로부터 arcs는 $A>B, B<A, B=C, C=B$로 결정될 수 있습니다.

2. Add all the arcs to an agenda.
   

3. Remove any inconsistent value from

3.1. Agenda의 A>B 조건을 먼저 살펴 봅시다.
A=1일때, 가능한 B의 값이 없습니다. 그렇기 때문에 1를 A에서 제거해줍니다. A=2,3는 A>B 조건을 만족하기 때문에 내버려 둡시다!
자, A의 도메인이 변경 되었기 때문에, 오른쪽에 A가 있는 Arcs를 살펴봅니다. B<A가 Arcs에 있습니다. 하지만 B<A는 이미 Agenda에 있기 때문에 추가할 필요 없이 다음단계로 넘어갑니다.

3.2. Agenda의 B<A 조건을 살펴 봅시다.
B=1일때 A=2,3이 만족합니다. B=2일때는 A=3이 만족합니다. 하지만 B=3일때는 만족하는(possible) 값이 없기 때문에 3을 B에서 제거해줍니다.
B의 도메인이 변경 되었기 때문에, 오른쪽에 B가 이는 Arcs를 살펴봅니다. A>B와 C=B가 있네요. A>B가 Agenda에 없기 때문에, A>B를 Agenda에 추가해줍니다. C=B는 Agenda에 있기 때문에 추가할 필요 없이 다음단계로 넘어갑니다.

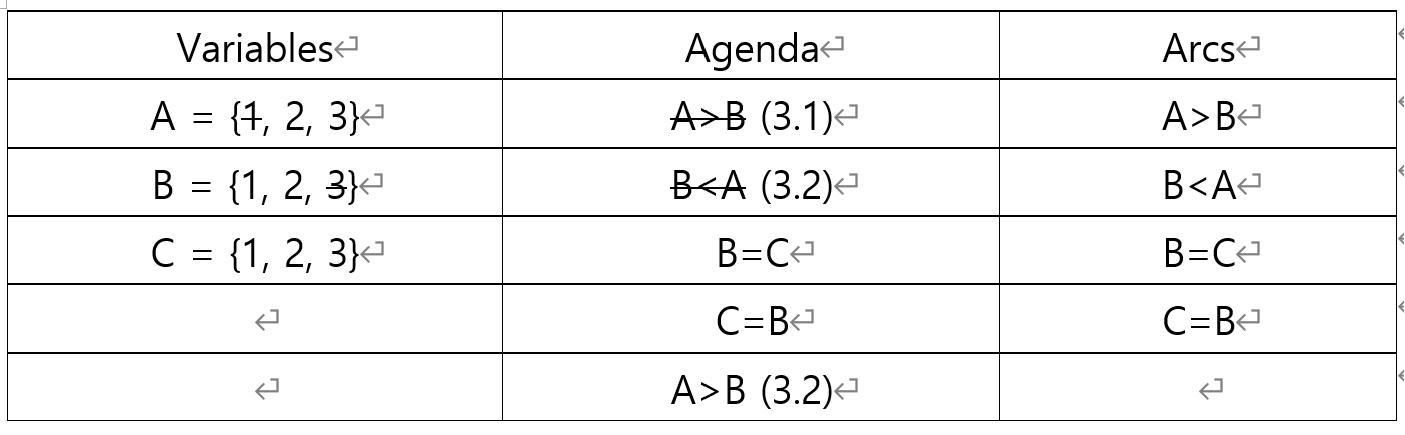
3.3. Agenda의 B=C 조건을 살펴 봅시다.
B=1일때 만족하는 C의 값이 있습니다. B=2일때 만족하는 C의 값 역시 있습니다. C=3인 경우는 extra이기 때문에 고려할 필요 없이 넘어갑니다. 도메인이 변경되지 않았기 때문에 Agenda에 추가할 필요 없이 다음 단계로 넘어갑니다.

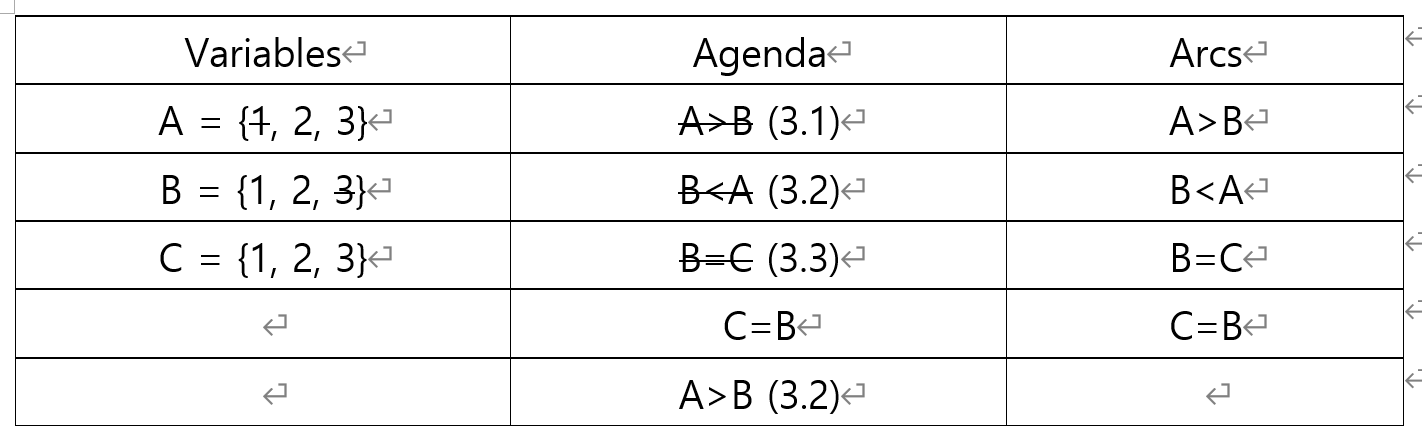
3.4. Agenda의 C=B 조건을 살펴 봅시다.
C=1,2 일때, B는 만족합니다. 하지만 C=3인 경우 가능한 B값이 없기 때문에 3을 C에서 제거해줍니다.
C의 도메인이 변경 되었기 때문에, 오른쪽에 C가 있는 Arcs를 살펴봅니다. B=C 하나 있네요. B=C가 Agenda에서 이미 제거되어 없기 때문에, B=C를 추가해줍니다.

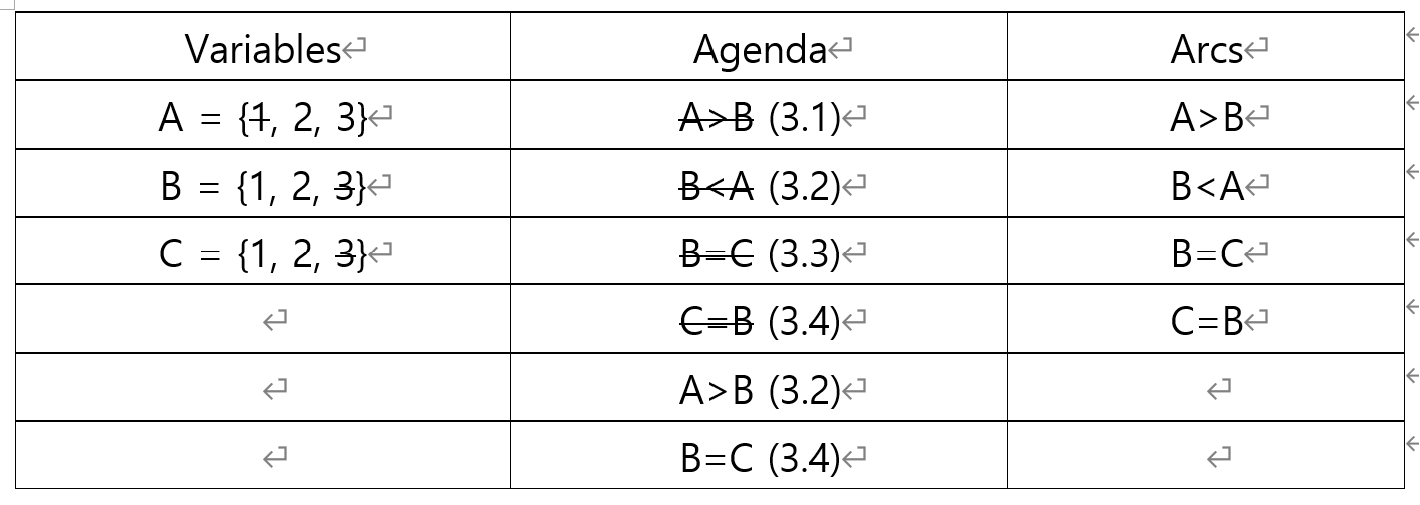
3.5. Agenda의 A>B 조건을 살펴 봅시다.
모든 값이 만족하기 때문에 변수의 도메인 변화 없이, 제약조건을 제거해줍니다.

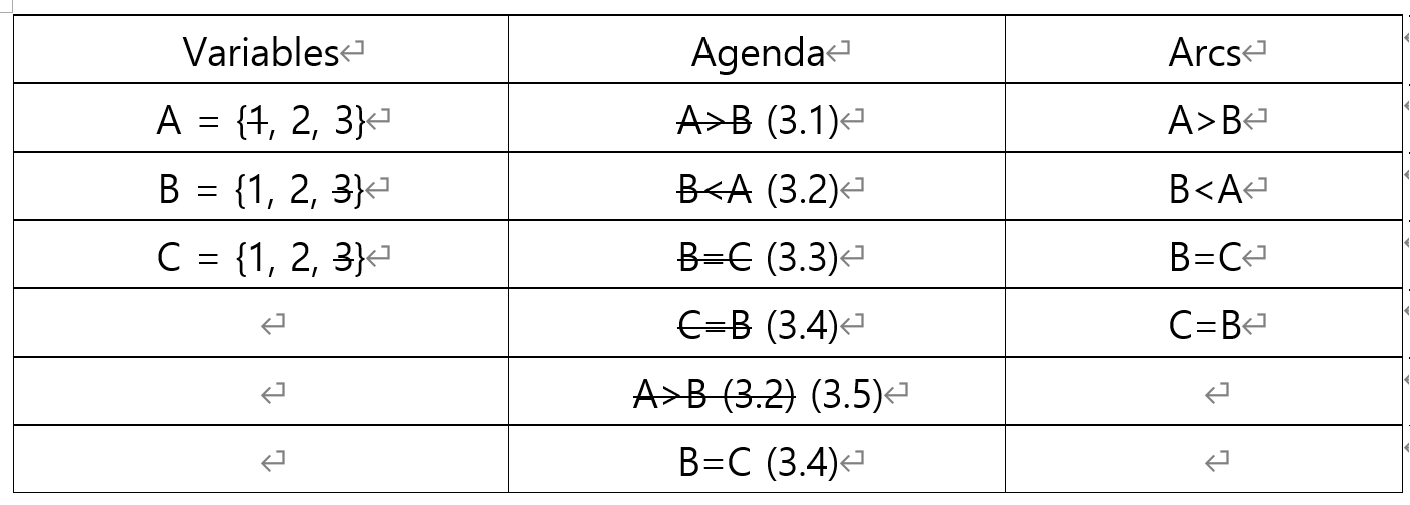
3.6. Agenda의 B=C 조건을 살펴 봅시다.
역시 모든 값이 만족하기 때문에 제약 조건을 제거해줍니다.

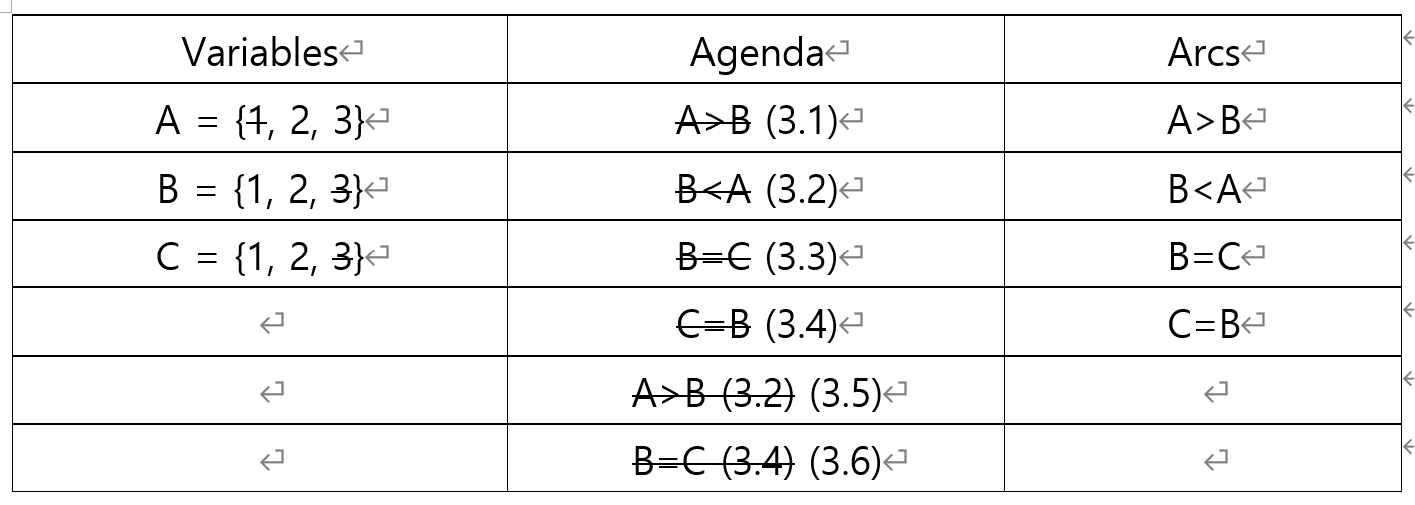
4. 자 Agenda 탐색을 끝냈습니다.
   이렇게 $A$={2,3}, $B$={1,2}, $C$={1,2}로 결론 지을 수 있습니다.