[Supervised Learning] K-Nearest Neighbour Algorithm (K-NN)

K-Nearest Neighbours(K-NN) 알고리즘은 머신러닝 분야에서 사용되는 학습 알고리즘 중 하나입니다. k-NN은 classification 혹은 regression 문제를 해결하는데 사용될 수 있습니다.

K-NN 개념

다음과 같이 파란색 네모, 빨간색 세모가 map에 있을 때, 새로운 데이터 초록색 동그라미가 어떤 카테고리로 구분 되어야하는지 알고싶습니다. 과연 파란색 네모로 구분해야할까요? 아니면, 빨간색 세모로 구분해야할까요?

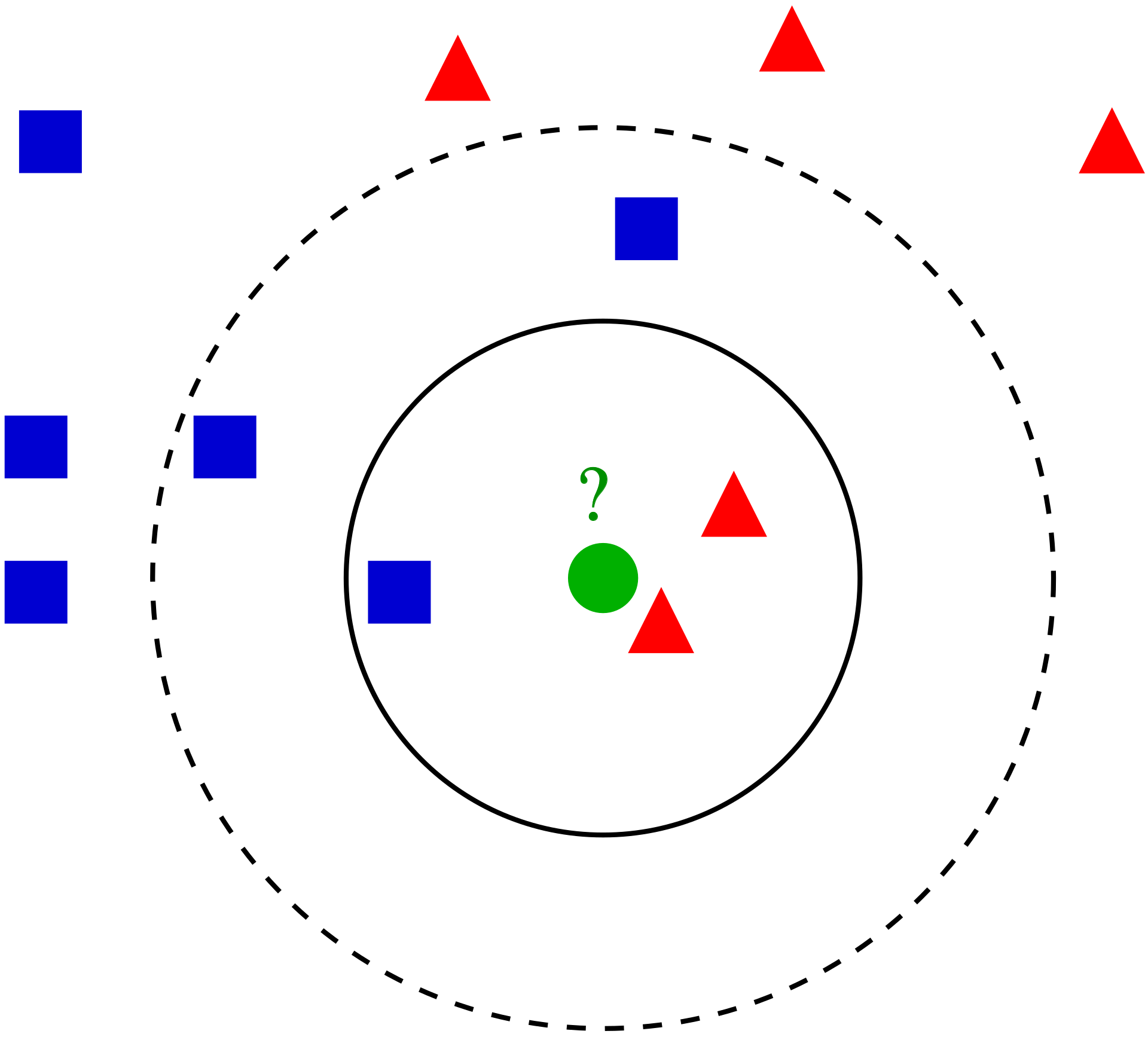
K-NN이란 데이터로부터 거리가 가까운 K개의 다른 데이터의 레이블을 참조하는 거리기반 알고리즘입니다.

다음 위의 예시에서, 만약 K가 2라고 했을 때, 가까운 2개의 데이터의 레이블은 빨간색 세모이기 때문에, 빨간색 세모라고 분류할 수 있습니다.

만약 regression 문제라면, 가까운 2개의 데이터의 평균을 사용하여 보통 새로운 값을 예측합니다.

거리 측정 (Distance Measure Method)

K-NN 알고리즘은 거리를 기반으로 데이터를 분류하거나 예측합니다. 그렇다면 가까운 거리를 계산할까요? 거리를 계산하는 여러가지 메소드가 존재합니다. 일반적으로는 유클리드 거리(Euclidean Distance)이나 맨하탄 거리(Manhattan Distance) 거리 측정 방법을 사용합니다.

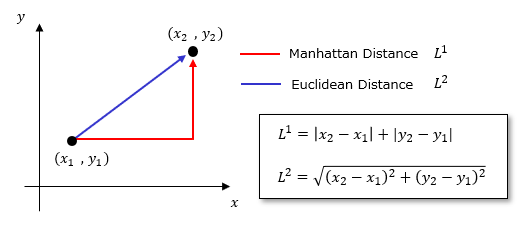
예를 들어, 데이터 $A(x_1, y_1)=(1,1)$, $B(x_2, y_2)=(4,4)$라고 가정합니다.

유클리드 거리 측정 (Euclidean Distance)

유클리드 거리 측정은 $L^2$ 공식을 사용하여 계산할 수 있습니다.
$\sqrt{(4-1)^2 + (4-1)^2} = \sqrt{9+9} =\sqrt{18}$

맨하탄 거리 측정 (Manhattan Distance)

맨하탄 거리 측정은 $L^1$ 공식을 사용하여 계산할 수 있습니다.
$|4-1|+|4-1| = 6$

K-NN 장단점

K-NN은 매우 직관적이고, 간단한 알고리즘이기 때문에 sample 데이터가 작은 경우 효율적입니다.

하지만 sample 데이터가 많은 경우, 훈련하는데 시간이 많이 소요됩니다. 또한, 훈련 시 이상치와 노이즈 데이터가 많이 섞여있었다면, 최종적으로 새로운 데이터에 대해서 분류 혹은 예측 시, 정확도가 많이 떨어지게 됩니다. 추가적으로, 거리를 기반으로 하기 때문에 데이터가 high dimension 구조일 때, 잘 작동하지 않습니다.