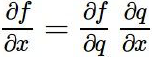4강. Introduction to Neural Networks
Computational Graph의 결과값을 역산하여 Gradient를 구하는 Backpropagation 방법과 Nerual Network의 개념에 대해서 다루었습니다.
CS231N - 4강
- Backpropagation
- Neural Networks
Backpropagation
Backpropagation (역전파)는 Linear Classification 연산의 결과를 역산하여 Gradient를 구하는 Analytic Gradient 방법론입니다.
Why Backpropagation?
Numerical Gardient의 대용량 Data 취약성과 낮은 정확성을 극복하기 위해 Analytic Gradient 방법론이 필요합니다.
Numerical Gradient의 한계
Numberical Gradient는 Gradient 연산이 쉽고 간편하지만, 모든 Dimensen에 대해 연산을 각각 진행해줘야 하므로 Data의 크기가 커지게 되면, 속도의 저하가 크다는 한계가 있습니다.
Analytic Gradient의 필요성
계산 과정은 복잡하지만 미분 연산을 통해 Weight Metric 자체의 Gradient를 바로 구할 수 있는 Analytic Gradient 방법론이 대용량 Data를 다루는 Neural Networks에 더 적합합니다.
Backpropagation?
Backpropagation은 (Full Loss)를 구하는 Computational Graph를 편미분 연산을 통해 역산함으로써 각 부분에 해당하는 Gradient를 구하는 방법입니다.
Computational Graph
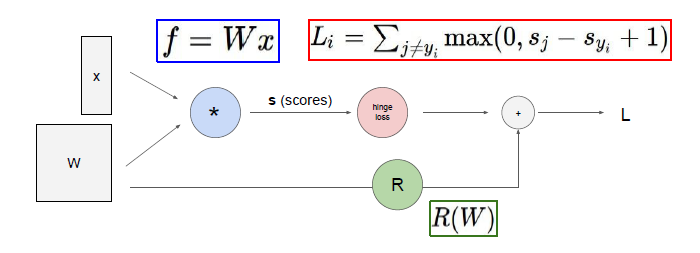
- (Score Function)
: 입력값과 Weight 간의 행렬곱을 통해 Class Score를 도출하는 부분입니다. - (Loss Function)
: 정답 Class와 각 Class의 Score 비교를 통해 Loss를 측정하는 부분입니다. - (Regularization)
: Overfitting을 방지하기 위해 Loss를 추가하는 패널티입니다.
Backpropagation의 원리
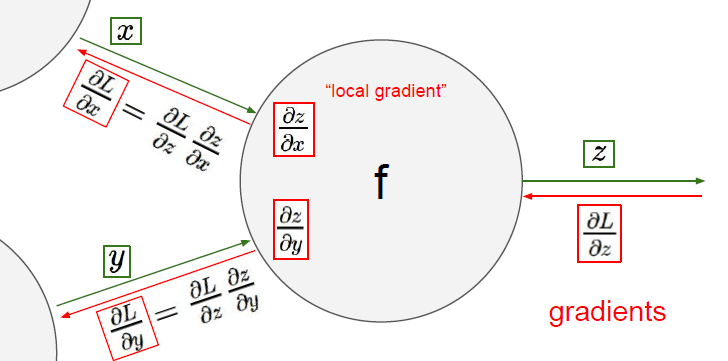
Computational Graph를 연산하게 되면, 위 사진의 입력값 , 가 정해진 연산식에 따라 연산결과로 를 도출하게 됩니다.
이때, Backpropagation은 결과값과 입력값 사이의 편미분 연산을 통해 와 값의 변화가 에 미치는 영향, Gradient를 구하는 것입니다.
간단한 예시를 통해 자세히 알아보겠습니다.
Backpropagation 연산 예시
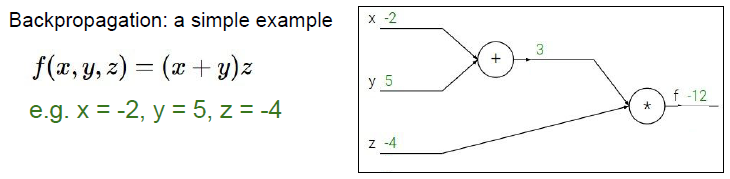 위 사진처럼 함수식과 그 Computational Graph 연산 결과가 있을 때, 저희가 구해야 하는 것은 가 결과값 에 미치는 영향, , , 입니다.
위 사진처럼 함수식과 그 Computational Graph 연산 결과가 있을 때, 저희가 구해야 하는 것은 가 결과값 에 미치는 영향, , , 입니다.
 가장 먼저 결과값과 결과값 간의 편미분, 는 1이므로 해당 위치에 1을 적어줍니다.
가장 먼저 결과값과 결과값 간의 편미분, 는 1이므로 해당 위치에 1을 적어줍니다.
 다음으로 입력값 와 결과값 간의 편미분, , 는 각각 3, -4입니다.
다음으로 입력값 와 결과값 간의 편미분, , 는 각각 3, -4입니다.
이때, 와 를 구하는 것은 다른 방식의 접근이 필요한데, 그 이유는 함수식을 그대로 편미분한다고 해도 다른 2개의 변수가 남아 Gradient 값을 구할 수 없기 때문입니다.
따라서 1단계 편미분 이후 2단계 역산부터는 Chain Rule이라는 새로운 방식을 사용하여 편미분 값을 구할 수 있습니다.
Chain Rule
Chain Rule은 3개 이상의 변수를 가진 식의 편미분을 유도하기 위해 편미분 식을 2개로 분리하여 진행하는 규칙입니다.
따라서, 위 사진처럼 를 구할 경우에는 의 하위 변수이자 의 상위 변수인 의 편미분 값을 경유함으로써 원하는 값을 구할 수 있습니다.
이때, 경유값에 해당하는 를Local Gradient, 상위값에 해당하는 를Global Gradient라고 부릅니다.
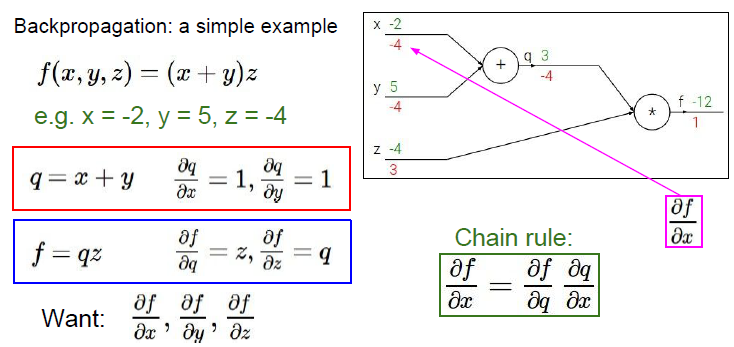 이렇게 Chain Rule을 적용하게 되면, 는 를 통해, 는 를 통해 구함으로써 원하는 편미분 값들을 모두 구할 수 있습니다.
이렇게 Chain Rule을 적용하게 되면, 는 를 통해, 는 를 통해 구함으로써 원하는 편미분 값들을 모두 구할 수 있습니다.
그리고 이렇게 구한 가장 하위 단계의 편미분 값들을 모두 더하면, 함수식 의 Gradient를 구할 수 있습니다.
Backpropagation pattern
Backpropagation은 각 gate의 특성에 따라 특정한 패턴을 가집니다.
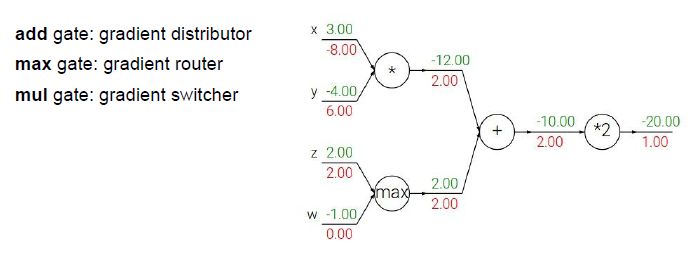
- Add Gate
: Global Gradient를 하위 단계 Gradient로 분배합니다. - Max Gate
: Global Gradient를 더 큰 Computation 값을 가지는 쪽으로 전달하고, 다른 방향에는 0을 전달합니다. - Mul Gate
: Global Gradient와 Local Gradient의 연산값을 원래 방향이 아닌 반대 방향으로 전달합니다.
또한, 한 Gate에 전달되는 Global Gradient가 2개 이상인 경우에는, Global Gradient의 합을 취합니다.
Backpropagation의 적용
이제 Backpropagation을 행렬 데이터와 행렬 연산식에 적용해보겠습니다.
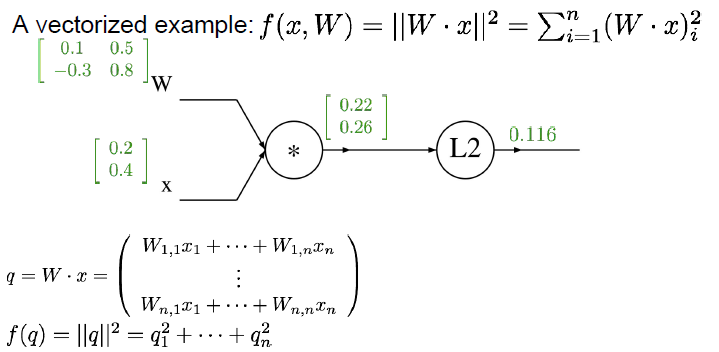 다음과 같이 행렬 변수인 로 이루어진 연산식과 그 Computational Graph 연산값들이 있습니다.
다음과 같이 행렬 변수인 로 이루어진 연산식과 그 Computational Graph 연산값들이 있습니다.
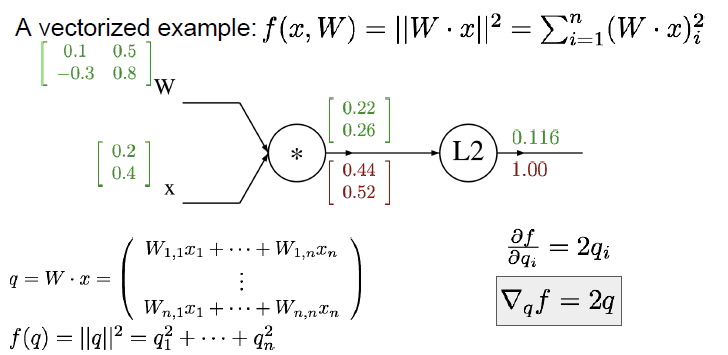 1단계 Gradient는 당연히 1이고, 2단계 연산값인 는 들의 합, 다시 말해 를 통해 구할 수 있습니다.
1단계 Gradient는 당연히 1이고, 2단계 연산값인 는 들의 합, 다시 말해 를 통해 구할 수 있습니다.
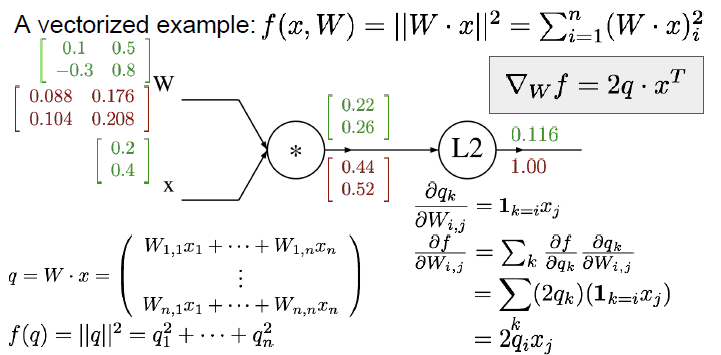
3단계 연산값부터는 Chain Rule를 적용할 필요가 있습니다. 따라서 는 Global Gradient인 와 Local Gradient인 의 곱을 통해 구할 수 있습니다.
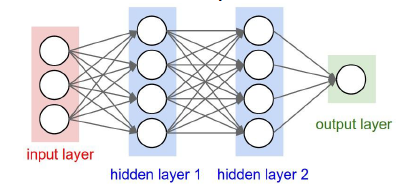
Neural Networks
Neural Networks는 여러 개의 Score Function,
Layer의 결합으로 이루어져 있습니다.
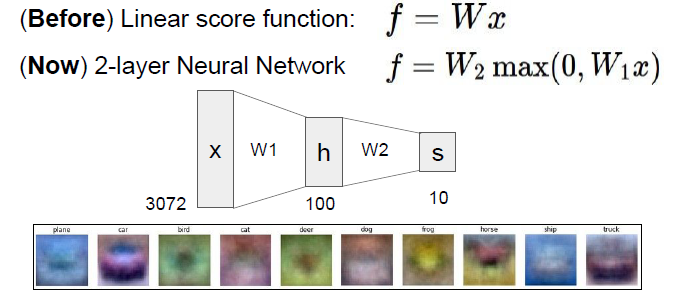 지금까지의 Linear Classifier가 하나의 Score Function으로 이루어져 있었다면, Neural Network는 한 Score Function의 결과값이 다른 Score Function의 입력값이 되는 Multi Layer의 형태로 구성되어 있습니다.
지금까지의 Linear Classifier가 하나의 Score Function으로 이루어져 있었다면, Neural Network는 한 Score Function의 결과값이 다른 Score Function의 입력값이 되는 Multi Layer의 형태로 구성되어 있습니다.
예를 들어, Image Classifier의 목표가 Class "Car"의 판독이라고 할때, 기존의 1-Layer Neural Network는 Class "Car"를 판독하기 위한 Weight Metric를 형성하지만, 다양한 형태와 색상의 차량에 대해 정확하게 판독하기는 어렵습니다.
하지만, Multi Layer Neural Network의 경우에는 1번 Layer에서 "Red Car", "Blue Car" 등 다양한 색상을 검출하는 Weight Metric를 구성하고, 이후 Layer에서 판독 결과들을 합치는 등의 방식으로 다양한 형태의 데이터에 대응하는 것이 용이합니다.
오타, 오역 등 지적은 언제나 환영입니다.