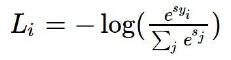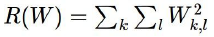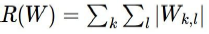3강. Loss Function and Optimization

Linear Classifier의 정확도를 측정하는 Loss Function과 이를 기반으로 W의 최적값을 찾기 위한 Optimization 방법론에 대해 다루었습니다.
CS231N - 3강

• Loss Function
• Optimization

---

Loss Function

Loss Function은 Linear Classifier Score의 차이에 집중하는 SVM과 각 Class에 속할 확률로 접근하는 Softmax 방법론이 있습니다.

Why Loss Function?

Linear Classifier는 Weight 값에 따라 Classification 결과가 영향을 받습니다.

그렇기에 위 사진처럼 가장 높은 Score를 가진 Class가 정답 Class가 아닌 경우에는 Weight 값을 조정할 필요가 있습니다.

이 때, Miss Classification의 감지와 그 정도를 파악하기 위해 사용되는 방법이 Loss Function입니다.

---

SVM (Support Vector Machine)

SVM은 정답 Class Score 값과 오답 Class Score 값의 차이를 중심으로 Loss를 계산하는 방법론입니다.

Train Data의 형태

$\{(X_i, Y_i)\}$

• $X_i$ : Image Data (Pixel Size)
• $Y_i$ : 해당 Image의 정답 Class 값

SVM의 형태

$L = \frac{1}{N}\sum_{i}L_i(f(X_i, W),Y_i)$

• $L$ : Linear Classifier의 평균 Loss
• $L_i$ : 해당 Data의 Classification Loss
• $X_i$ : Image Data (Pixel Size)
• $Y_i$ : 해당 Image의 정답 Class 값

SVM은 Image Data의 Score 값과 정답 Score 간의 연산을 통해 각 Data의 Loss를 구하고, 전체 Loss에 대해 평균값을 취하는 방식으로 이루어집니다.

SVM의 Loss 정의

Linear Classifier의 결과로 얻은 각 Class의 Score들과 정답인 Class의 Score 사이의 차이를 Loss로 정의합니다.

SVM 연산

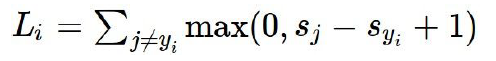
• $S_j$ : 해당 Class의 Score 값
• $S_{yi}$ : 정답 Class의 Score 값

SVM 연산은 정답 Class와 해당 Class의 Score값의 차에 오차 범위 1을 더하고, 그 값과 0중 더 큰 값을 취하는 방식으로 이루어집니다.

SVM Loss의 최소값
SVM Loss는 정답과 오답의 Score 차이이기 때문에 정답 Class에 대해서는 Loss 값이 0으로 도출됩니다.

SVM Loss의 최대값
오답 Class의 Score가 무한대 값을 가질 경우, max function으로 인해 Loss 값은 양의 무한대로 도출됩니다.

SVM의 특성

SVM에서 Loss는 Score 간의 차이가 얼마나 나는지보다, 어떤 Class와 Class 사이에 차이가 존재하는지에 중점을 맞추고 있습니다.

이로 인해, SVM은 Weight이나 Score의 값에 작은 변화가 있더라도 Loss 값에 큰 변화가 없습니다.

---

Softmax Classifier

Softmax Classifier는 Data가 각 Class에 속할 확률을 Score로 취하고, $-log$ 값을 Loss로 도출하는 방법입니다.

Softmax Classifier의 형태

• $e^sy_i$ : 정답 Class Score에 Exp를 취한 값입니다.
• $e^sj$ : j번째 Class Score에 Exp를 취한 값입니다.
• $\frac{e^sy_i}{\sum_je^sj}$ : 각 Class에 속할 확률로 정규화되지 않은 확률값입니다.

Softmax Classifier의 연산

Softmax Classifier 연산은 Class Score 값에 Exp를 취해 log를 해제하는 단계와, 그 이후 비정규 확률값을 정규화해주는 과정, 마지막으로 정답 Class에 $-log$를 취해 Loss값을 도출하는 방식으로 이루어집니다.

Softmax Loss의 최소값
Softmax Loss의 최소값은 정답 Class에 속할 확률이 100%, 즉, 1인 경우이므로 그 $-log$값인 0입니다.

Softmax Loss의 최대값
Softmax Loss의 최대값은 정답 Class에 속할 확률이 0%,즉, 0이므로 그 $-log$값인 무한대입니다.

Softmax Classifier의 특성

SVM과 달리 Softmax는 각 Class에 속할 확률의 합이 1로 고정되어 있기 때문에 작은 Score나 Weight 값의 변동에도 Loss 값에 변화가 일어난다는 특성을 가집니다.

---

Regularization

Regularization (정규화)는 Classification의 결과가 Overfitting이 되지 않도록 모델을 간소화시키기 위해 학습 과정에서 사용하는 Penalty입니다.

Why Regularization?

Loss Function 만을 이용해서 Classification을 진행하게 되면, 위 사진처럼 Classification의 결과가 Train Data에 지나치게 적합한 Overfitting 문제가 발생할 수 있습니다.

따라서 학습 결과가 Train Data에 완벽히 적합하지 못하도록 하는 일종의 장애물, Regularization을 통해 Classification의 정확도를 조금 포기하는 대신 단순성과 범용성을 취합니다.

Regularization의 종류

L2 Regularization

Weight Metirc Data의 Square(제곱)를 Loss Function에 더해줌으로써 실제 Loss보다 Loss를 보수적으로 측정하게 합니다.

L1 Regularization

Weight Metirc Data의 절대값을 Loss Function에 더해줌으로써 실제 Loss보다 Loss를 보수적으로 측정하게 합니다.

---

Loss의 구조

Loss는 Score Function의 결과, Score를 Loss Function입력해 구한 $L_i$를 Regularization으로 정규화함으로써 구할 수 있습니다.

1. Score Function
Input Image Data와 Weight 간의 연산을 통해 각 Class의 Score를 구합니다.

2. Loss Function
각 Class의 Score 값들로부터 각 Class의 Loss, $L_i$을 구합니다.

3. Regularization
Regularization으로 Loss에 추가적인 Loss를 더하여 보수적으로 Loss를 측정합니다.

---

Optimization

Loss Function을 통해 구한 Loss를 토대로 최적의 Weight값을 찾아야 합니다.

Random Search

최적의 Loss가 도출될 때까지 Weight Data를 변화시키면서 Loss를 구하는 방법론입니다.

Random Search는 MxN 사이즈의 Weight Metric Data가 가질 수 있는 모든 가능성을 탐색하기에 최적 Weight를 찾을 수 있습니다.

하지만, 연산과정이 굉장히 길고, 비효율적이기에 실제로 사용하기에는 적합하지 않습니다.

---

Gradient Descent

Loss Function 상에서 Weight를 지속적으로 이동시키면서 Loss가 최소값이 되는 Weight를 찾는 방법론입니다.

Gradient Descent의 원리

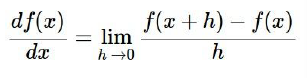
• $f(x)$ : 최소값 탐색의 대상이 되는 함수
• $h$ : 탐색 시마다 이동하는 거리 (Step size)

Gradient Descent는 함수 상에서 해당 함수가 최소값을 가질 때까지 조금씩 이동하면서 탐색을 실행하는 방법론입니다.

Step Size Issue
Step Size ($h$)가 클 경우, 빠르게 최소값 지점을 찾을 수 있다는 장점이 있으나 최적점을 지나치게 무한하게 증가할 수 있기에 적절한 크기의 Step Size를 설정하는 것이 중요합니다.

Numerical Gardient

Weight에 Step Size를 더하고, 미분을 통해 기울기 변화량을 측정하는 방법입니다.

각 Dimensen(차원) 마다 연산을 해주어야 하는 만큼 속도가 느리고 정확도가 낮지만, 간편하게 사용할 수 있습니다.

Analytic Gradient

Weight Metric 자체를 미분하여 Gradient를 구하는 방법입니다.

연산량이 상대적으로 적은 만큼 속도가 빠르고 정확도가 높지만, 계산식이 복잡해 에러의 가능성이 높습니다.

Gradient Descent의 적용

Gradient Descent는 Gradient 연산로 얻게 된 Gradient dW를 Step Size만큼 곱한 후 Weight에 더해주는 방식으로 이루어집니다.

이때, Loss Function 그래프의 반대 방향으로 이동해야 하기 때문에 곱할 때 (-) 부호를 곱해줍니다.

실행 결과

Stochastic Gradient Descent (SGD)

Data Size가 커지게 되면 Gradient를 계산하는 데 상당한 시간이 소요됩니다.

따라서, 실행 시간을 단축하기 위해 Mini Batch를 정하고, 그 안에서 연산을 진행하는 방식을 사용할 수 있습니다.

Mini Batch
$2^n$ 크기의 숫자로 Gradient 연산에 소요되는 시간을 줄이기 위해 임의로 설정한 Data Size입니다.

---

오타, 오역 등의 지적은 언제나 환영입니다.