Machine Learning Day 14
<Bayesian Inference>

<Bayesian Updating>
When a prior dataset can be roughly represented by a normal distribution, bayesian statistics show that sample information from the same process can be used to obtain a posterior normal distribution. The latter is a weighted combination of the prior and the sample.
<Bayes' Theorem>
P(A∣B)=P(B∣A)P(A)/P(B)
=> * Prior Probability: P(A)
=> * Likelihood : P(B∣A)
=> * Posterior Probability: P(A∣B)
=> * Unnorm Constant: P(B)=∑(jointprobabilities)
It can also be
P(A∣B)=P(A∩B)/P(B)
- Joint Probability: P(A∩B) = Likelihood x Prior Probability
사전확률을 어떤 행동의 관찰, 정보의 획득에 의해서 사후확률로 업데이트하는것: 베이즈 업데이트
Therefore,
P(B∣A)P(A)=P(A∩B)
<Exercise.1>
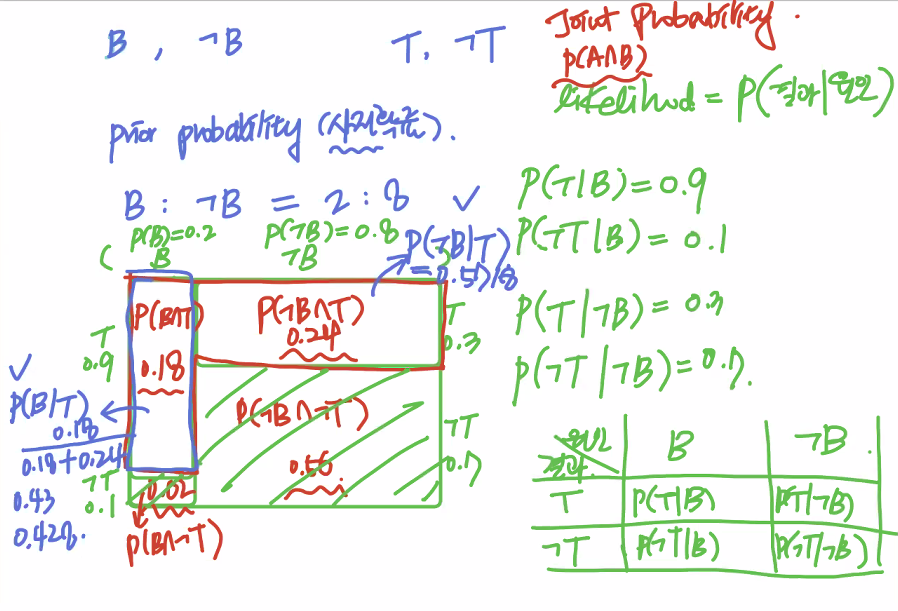
blue: posterial probability (0.428, 0.5718)
-> Probability grew two times bigger with just one more information. 20% -> 43%
<Exercise. 2>
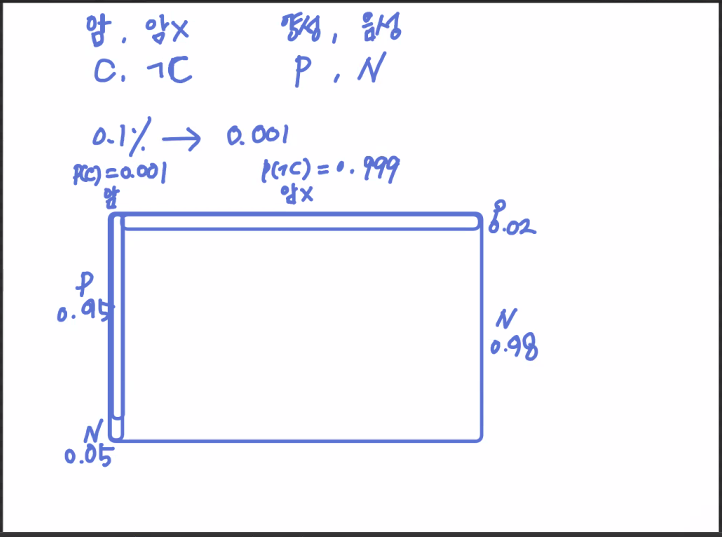
-
Prior Probability:
P(C)=0.001P(¬C)=0.999
-
Likelyhood:
P(P∣C)=0.95P(N∣C)=0.05P(P∣¬C)=0.02P(N∣¬C)=0.98
-
Joint Probability:
P(P∩C)=0.95×0.001=0.00095P(N∩C)=0.05×0.001=0.00005P(P∩¬C)=0.02×0.999=0.01998P(N∩¬C)=0.98×0.999=0.97902
-
Posterior Probability:
P(C∣P)=0.00095/(0.00095+0.01998)=0.04539P(¬C∣P)=0.01998/(0.00095+0.01998)=0.0955P(C∣N)=0.00005/(0.00005+0.97902)=0.00005P(¬C∣N)=0.97902/(0.00005+0.97902)=0.99995
<Exercise.3>
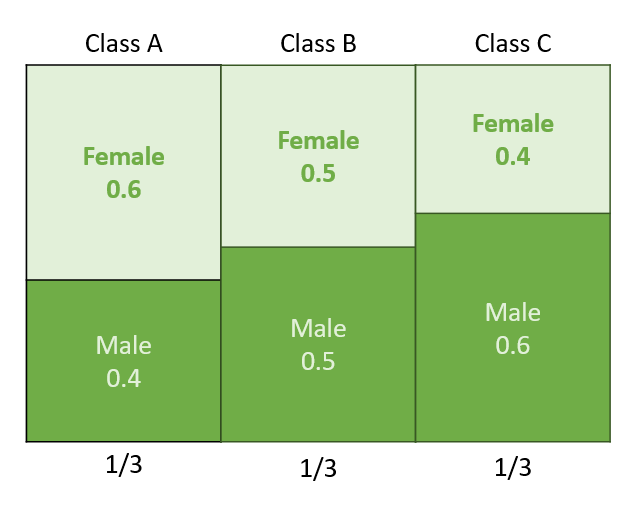
-
Likelihood:
P(F∣CA)=0.6P(M∣CA)=0.4P(F∣CB)=0.5P(M∣CB)=0.6P(F∣CC)=0.4P(M∣CC)=0.6
-
Joint Probability:
P(F∩CA)=0.6×1/3=0.2P(M∩CA)=0.4×1/3=0.1333P(F∩CB)=0.5×1/3=0.1666P(M∩CB)=0.5×1/3=0.1666P(F∩CC)=0.4×1/3=0.1333P(M∩CC)=0.6×1/3=0.2
-
Posterior Probability:
P(CA∣F)=0.2/(0.2+0.1666+0.1333)=0.40008P(CB∣F)=0.1666/(0.2+0.1666+0.1333)=0.33326P(CC∣F)=0.1333/(0.2+0.1666+0.1333)=0.26665



