시스템 모델링 및 제어 : 제어란 무엇인가

시험기간이라서 노션에 쓴 거 걍 올림. 후배들에게 잘 써먹히길 바랍니다...🥹

What is Control and “Why it Matters”?

Control Domains

---

-Flight Control

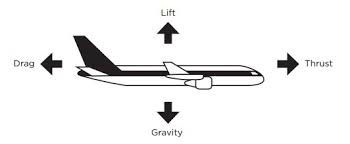
• 양력 : 비행기의 무게와 반대되는 힘. 중력보다 커야 비행 가능
• 항력 : 비행기가 앞으로 나아가지 못하게 하는 힘. 추력과 반대되며 추력보다 작아야함. (ex : 유도항력, 마찰항력)
• 추력 : 앞으로 나아가는 힘. 비행기가 움직이게 하는 원동력. 높은 추력으로 속도를 높이고 날개에 빠른 공기유동력을 가진다.
• 중력 : 지구가 비행기를 끌어당기는 힘. 무게 자체와 연관되어 있음.

Take - off

• 에어포일 상부와 하부의 압력차에 의한 양력이 발생함.
• 날개에 흘러들어오는 공기와 에어포일 사이의 각을 받음각이라 하며, 압력차로 인해 양력이 발생함.
• 받으각을 너무 크게 하면 항력이 더 커질 수 있으며 공기는 날개 단면을 따라 흐르지 못하고 분리되어 흘러 실속(속도를 잃어버림)할 수 있음.
• 방향타와 승강타를 이용해 꼬리의 수직력을 조절함

→ 이륙 필수 조건 : 양력, 높은 받음각, Flap&Slap 사용

Landing : Spolier로 공기저항을 높임

-Autonomous Vehicle Control

• 승차감을 위한 샤시 컨트롤
• Handling Safety

-UAV(Uninhabited Aerial Systems) & Drones

Control Basics

---

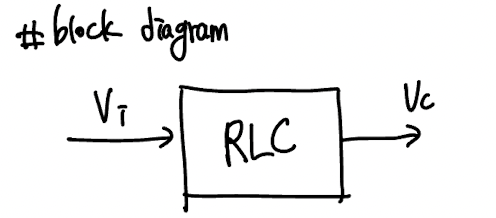
Block Diagrams

• 시스템의 input, output을 블록으로 설명함.
• 블록에는 플랜트의 동역학을 포함하지만 구체적으로 표현하지는 않음.

OpenLoop

• desired 결과값을 계산함.
• uncertain 값(오르막, 바람 등) 에 대하여 피드백 불가
• 복잡한 시스템에서는 정확한 값을 가져올 수 없음.
• 예시 :
  

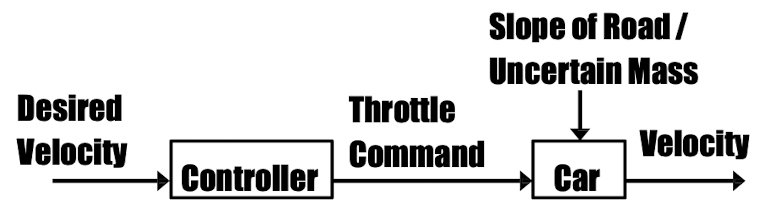
Close Loop/Feedback

• 현재 측정값을 반영하여 command 값을 계산해냄
• 그러나 trade off가 있음 : stability, speed of response, sensor noise rejection...
• 예시
  

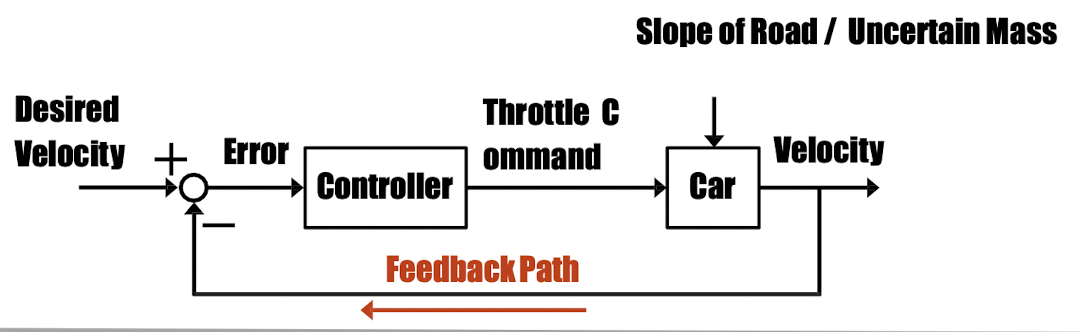
Cruise Control System Block Diagram

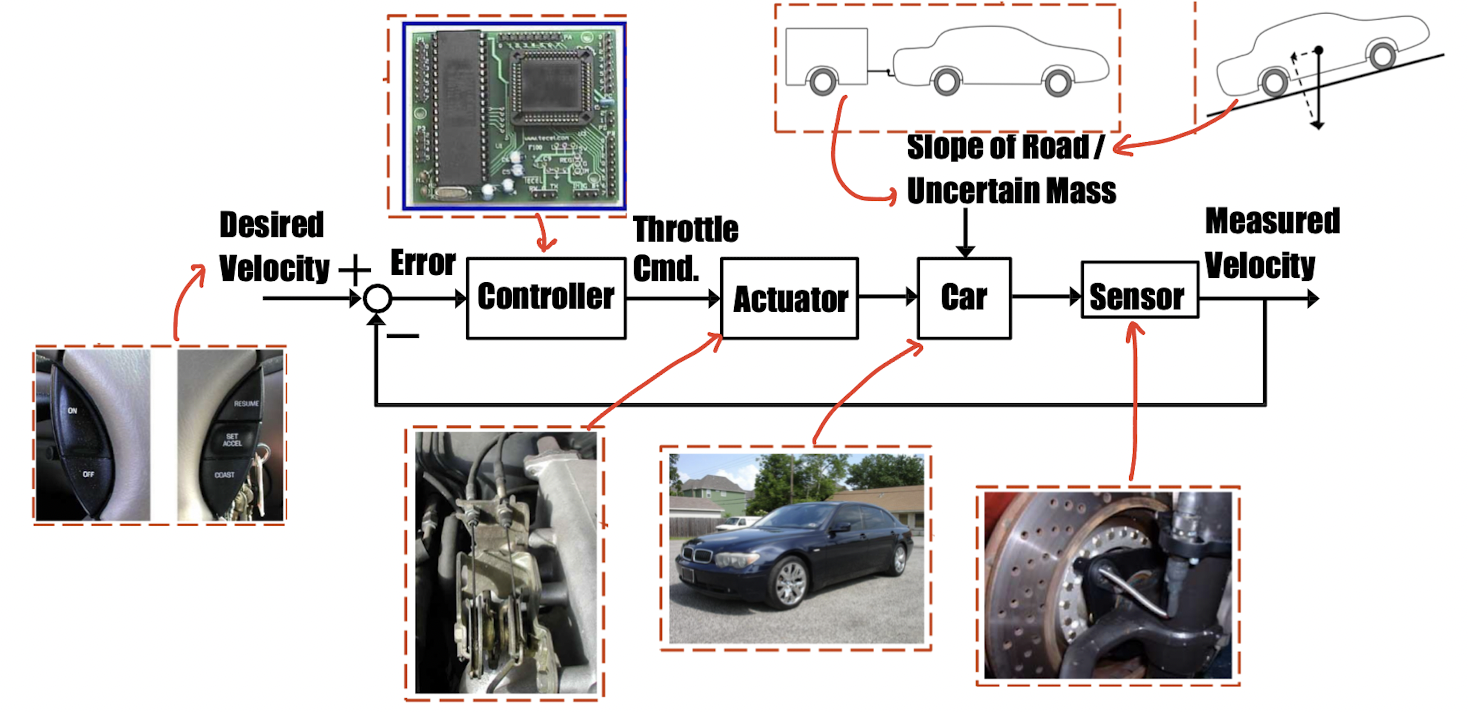
Control Design

→ 공학에서 Design은 미적인 디자인보다는 ‘설계’ 의 의미를 훨씬 더 강하게 내포하고 있음.

Design Process

1. Model the System : using Differential Equations
2. Design the Control Algorithm : PID 등
3. Analyze and Simulate : 이론, 시뮬레이터 사용
4. Implement the controller and experiment
5. Iterate

• Model은 단지 “approximation”일 뿐 현실에서 시스템을 검증해야함. → Model은 incorrecties를 가지며 control system 설계를 위해서는 simplest model(essential dynamics)를 정의해야함
  

Primary Method for Constructing Dynamic Models

1. First Principles : 물리법칙(뉴턴의 운동 제 2법칙 F=ma)
2. Black Box : Experimental input/output data와 연관
3. Grey Box : 1+2, 모델 파라미터를 구하기 위해 1,2방법을 모두 사용

• Modeling 은 “domain-specific”한 과정이다. 도메인에 따라서 모델링 스텝이 다름. 그러나 최종적인 model, equation 형태는 비슷함!
  
  
  

Modeling Practice

---

Mechanical System

→ Dynamics of Mechanical System은 대부분 뉴턴의 법칙을 따른다.

1. Moving Mass

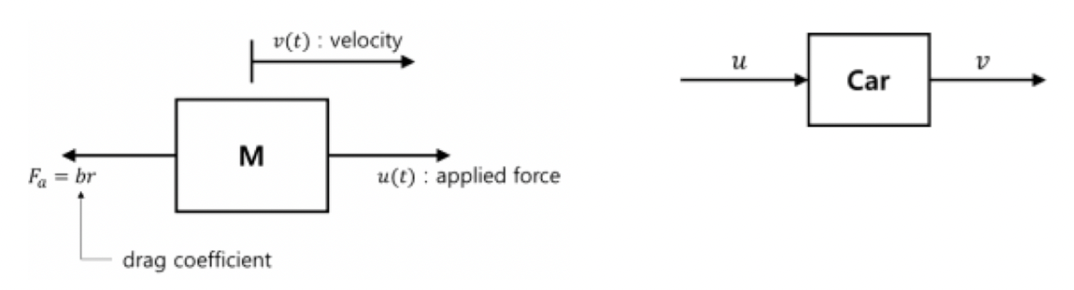
$F = ma =$ 추력 - 항력X속도

$m \dot{v}(t) = u(t) - bv(t)$

$\dot{v}(t) + \frac{b}{m}v(t) = u(t)$ : First Order ODE

→ 수학적으로 설명하기 좋은 형태로 변형함

• Linear Differencial Equation (Ordinary Differential Equation : ODE) : 시간에 따라 달라짐. v(t), u(t)에 대한 선형적인 의존성을 가짐.
  

• 시간 t에 대한 v(t)fmf dPcmrgkrl dnlgotjsms 1) t=0에 대한 v가 정해져야 한다 → Inital Condition 2) t=0~t=t 까지의 input을 알아야한다.
  

2. Mass-Spring-Damper
   

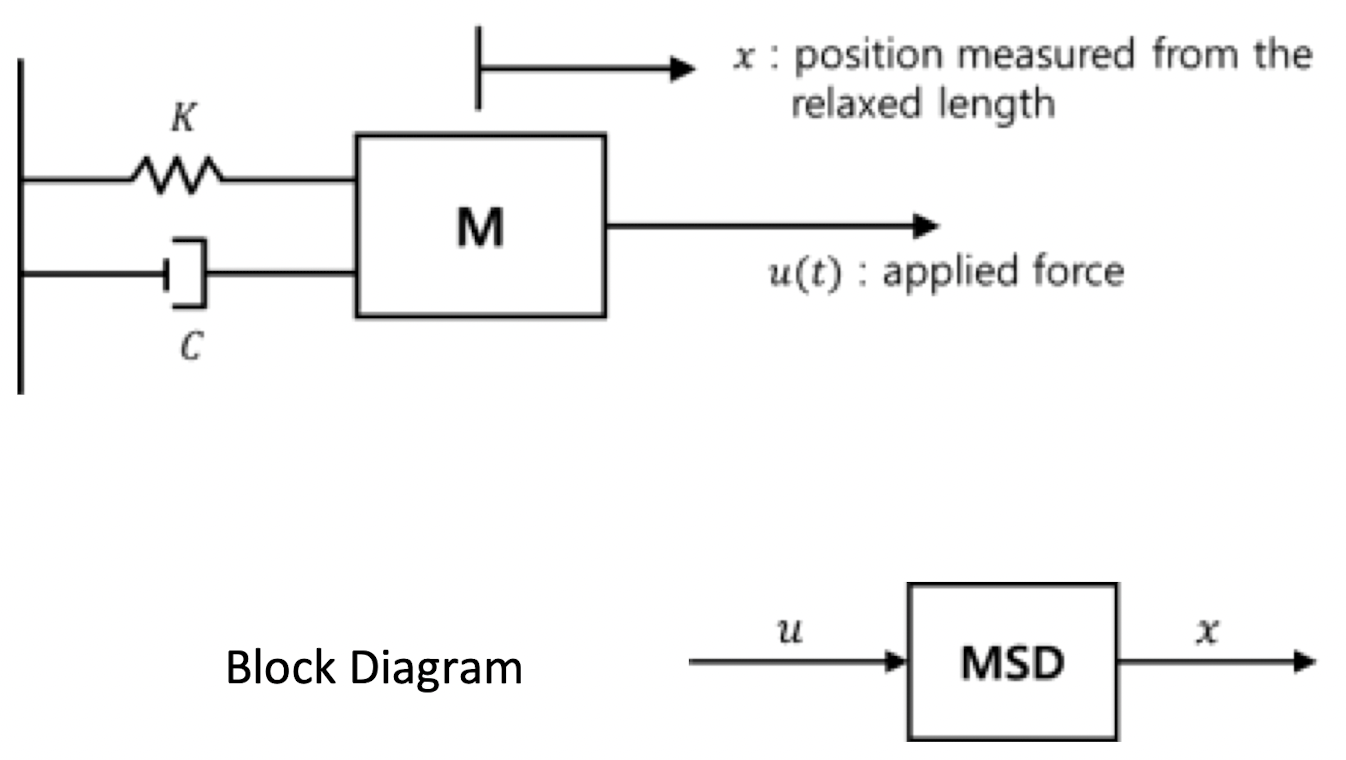
1) Linear(Hookean) Spring

2) Viscous Dampler

$F = k \cdot x$
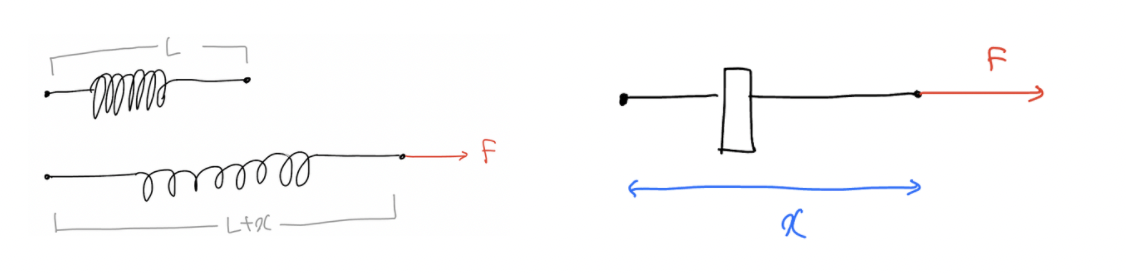
(k = spring coefficient)

$F = c \dot x$
(c = damper coefficient)

3) Free Body Diagram for Mass & Block Diagram

$m \ddot{x} = -kx -c \dot x + u$

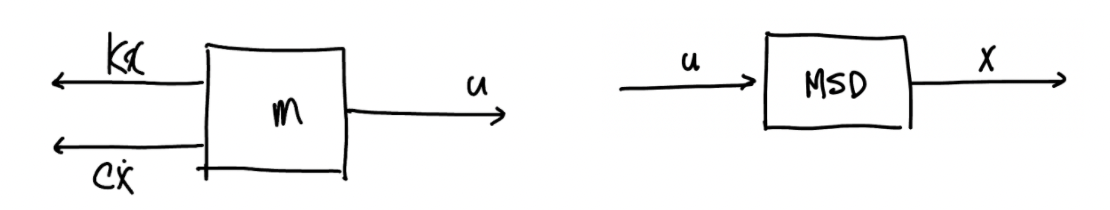
$\therefore \ddot{x} + \frac{c}{x}\dot x + \frac{k}{m}x = \frac{1}{m}u$ : 2nd Order ODE

$I.C = \begin{cases}x(0) = x_0\\\dot{x}(0) = v_0\end{cases}$

(오른쪽 블록 다이어그램)

Electircal System

→ Passive Electrical Components : Resister, Capacitor, Inductor

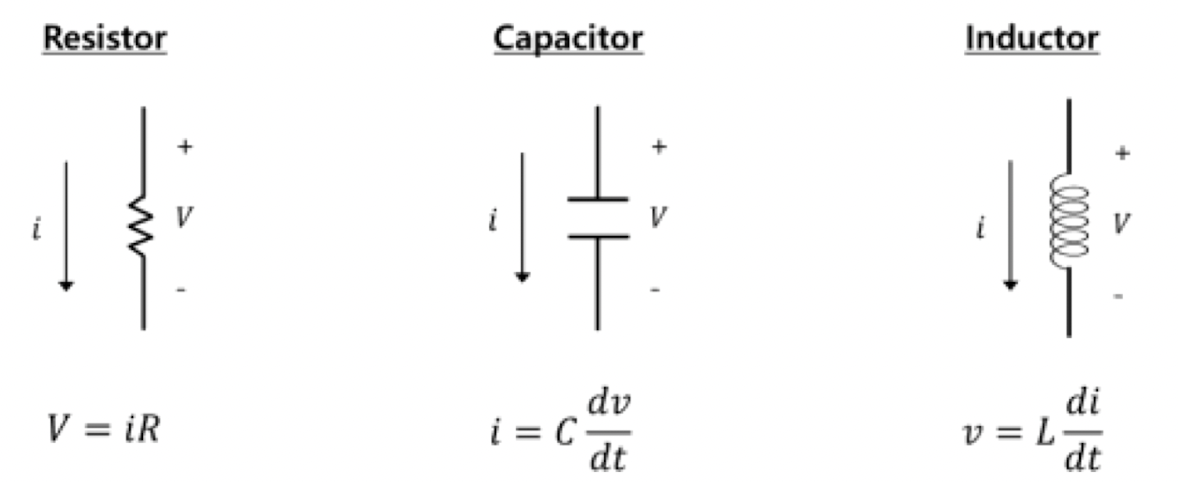
1. Kirchoff’s Current Law : KCL

   임의의 접점에서 모든 전류의 합은 0이다.

   Positive(+) : 노드를 나가는 전류 : $i_3$

   Negative(-) : 노드로 들어오는 전류 : $i_1, i_2$

   $\therefore i_3-i_1-i_2 = 0$

2. Kirchoff’s Voltage Law (KVL)

   폐회로에서 모든 전압의 합은 0이다.

   Positive : voltage drop : $v_3$

   Negative : voltage rise : $v_1, v_2$

   $\therefore v_3-v_1-v_2 = 0$

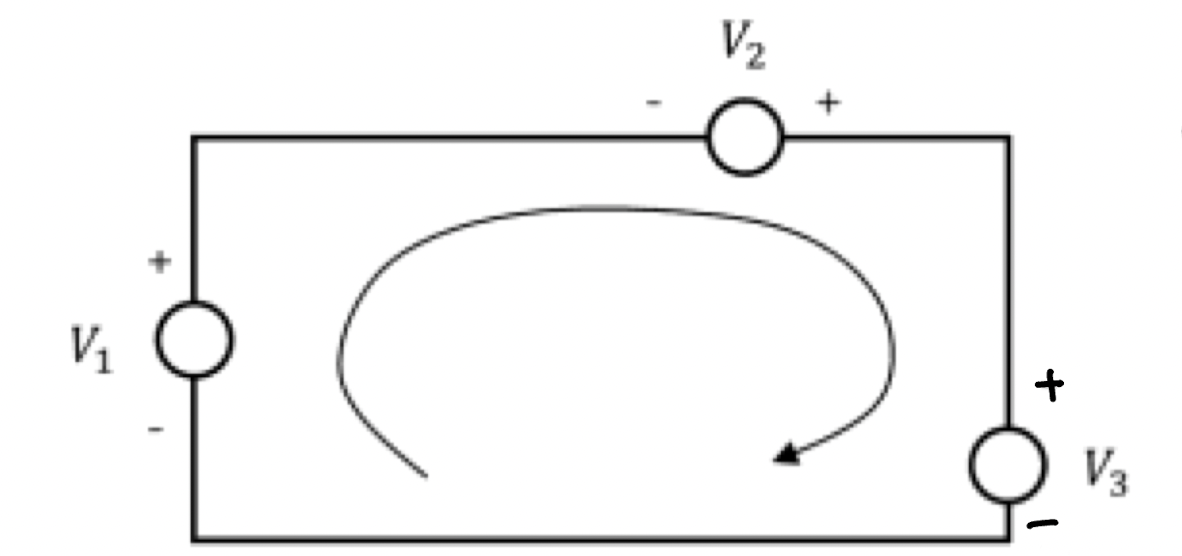
1. RLC Circuit

   *단, 모든 요소가 이상적이라고 가정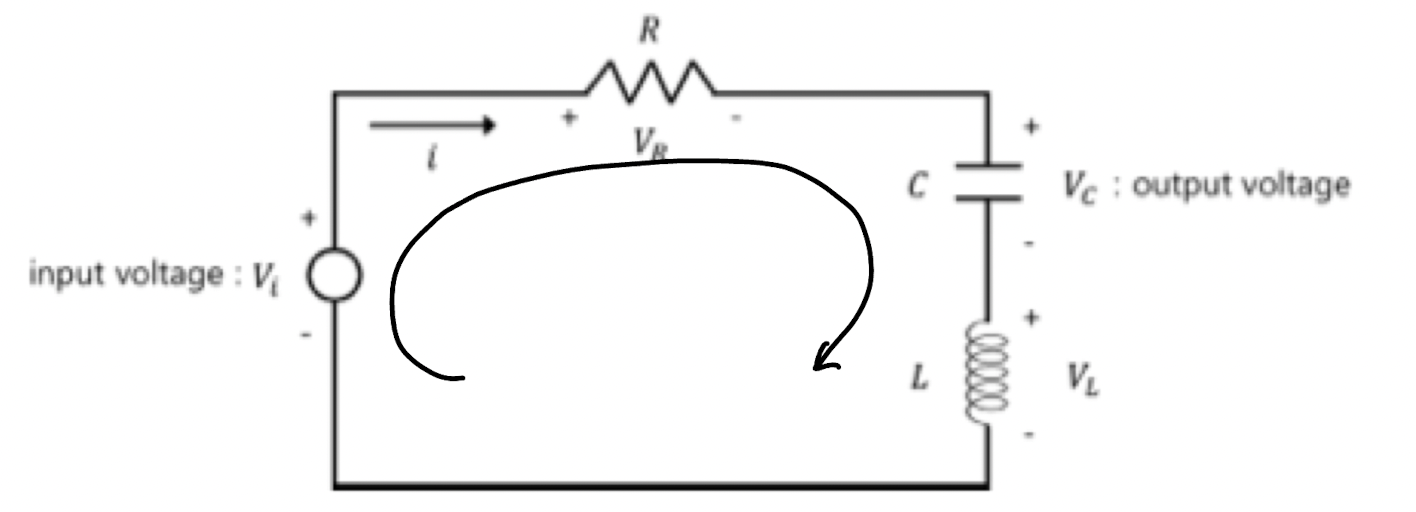

   

$V_R = iR \\ C \dot{V_c} = i \\ L\frac{di}{dt} = V_L$

$i = C \frac{dV_c}{dt}\\ V_R = R \cdot C\frac{dV_c}{dt}\\ V_L = LC$

$\therefore LC \frac{d^2V_c}{dt^2} + RC\frac{dV_c}{dt} + V_c = V_i$

$I.C = \begin{cases}V_c(0) =V_{c,0}\\\dot{V_c}(0) =\frac{i_0}{c}\end{cases}$

Aerodynamic Systems

→ 강체 뉴턴법칙(? Newton’s laws for the rigid body Dynamics)와 유체역학을 적용한다.

1. Lanchester Model for the Phugoid Dynamics

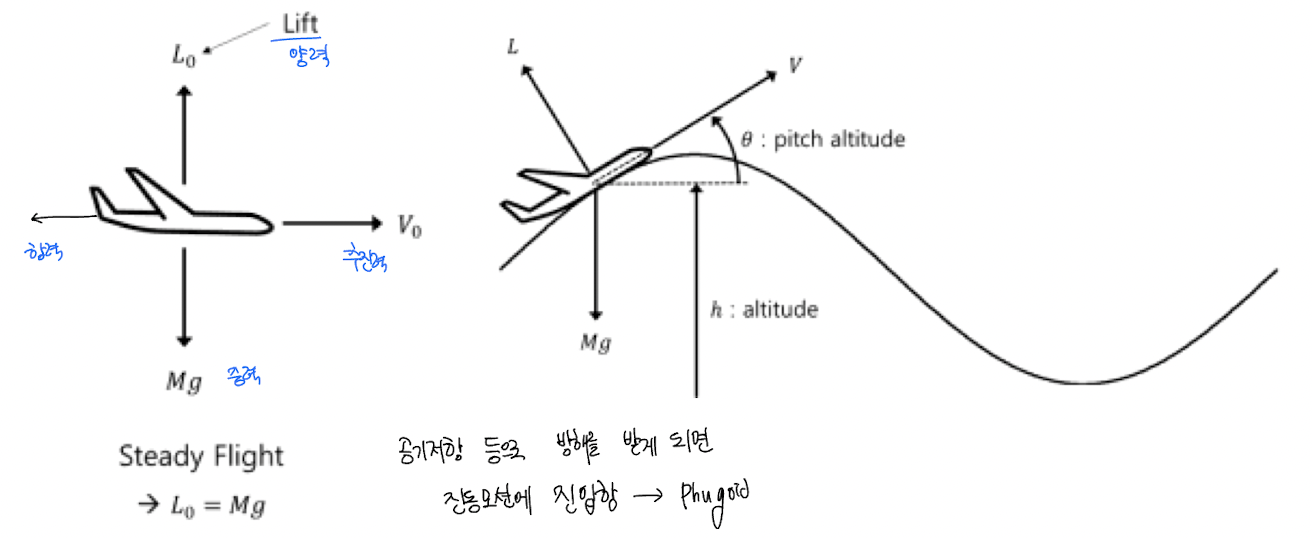
Assumption

1. 모든 에너지는 보존된다. (The Energy is Constant)

   $\frac{1}{2}m v_0^2 = \frac{1}{2}mv^2 + mgh$

   (inital kinetic E = kinetic E duing oscillation + potential E)

2. 양력은 $v^2$에 비례한다.(The lift force is proportional to $v^2$)

   $L = kv^2$

   k = standard aero notation

   $k = \frac{1}{2} \rho J C_l$ ($\rho$=공기밀도, J=단면적, $C_l$ = lift coefficient)

뉴턴의 제 2법칙에 의하여

$M\ddot{h} = L \cdot cos\theta - Mg$ (*)

1. 에 의하여 다음과 같이 쓸 수 있음

$v^2 = v_0^2 - 2gh$

ii. i. 에 의하여 다음과 같이 쓸 수 있음

$L = k v^2 = kv_0^2 - 2kgh$

Steady Flight 에서

L_0 = kv_0^2 = mg

$\therefore L=mg-2kgh$

*에 대입하면 다음과 같이 정의할 수 있다.

$M\ddot{h} = (Mg-2kgh)cos\theta - Mg$

+Assumption

pitch $\theta$ 는 매우 작음. ($cos\theta \approx 1$)

따라서 Lanchester Model로 Phugoid Motion 을 유발함.

$\ddot{h} = \frac{2kg}{M}h = 0$

→ Autonomous Model : 식의 우항이 0일 때(=input 이 0이다)

$I.C = \begin{cases}h(0) =h_0\\\dot{h}(0) =r_0\end{cases}$

($r_0$ = reference speed)

+) Phugoid 모드는 낮은 frequency 로 약하게 진동하는 것을 뜻하며 이 때 속도 u, pitch attitude $\theta$, 높이 h를 가진다.

비행기가 진동주기의 상점에 있을 때 속도가 느려지고, 하점에 있을 때 속도가 빠르다. (에너지보존법칙)

Summary

시스템은 Linear ODE로 표현 가능하다.

일반적인 n차 ODE는 다음과 같은 형태이다.

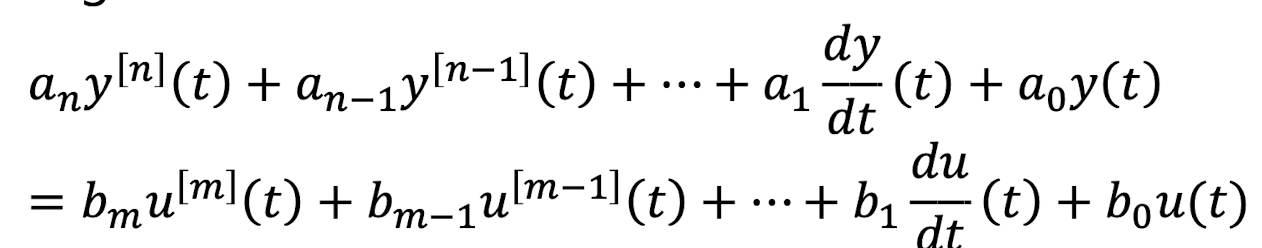
일반화를 위한 Assumption

1. $a_n \neq0, b_n \neq 0$

2. m ≤ n

   m : input term이 가진 항의 개수

   n : 미분 term이 가지고 있는 좌측 항의 개수

Initial Condition(I.C)

$I.C = \begin{cases}y(0) =y_0^{[0]}\\y^{[1]}(0) =y_0^{[1]}\\ \vdots\\ y^{[n-1]}(0) =y_0^{[n-1]}\\ \end{cases}$

→ $y^{[k]} =$ y의 k번째 미분 term → $y^{k}(t) = \frac{d^ky}{dt}(t)$