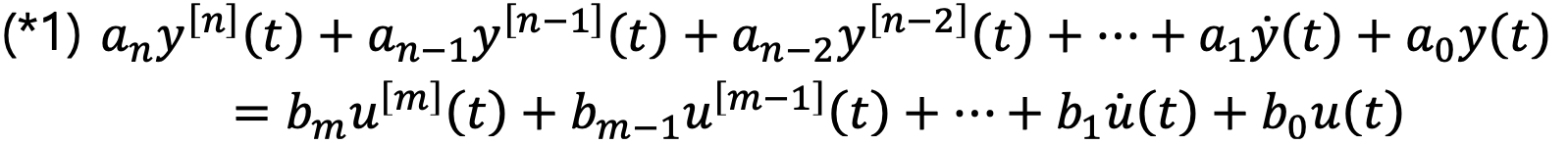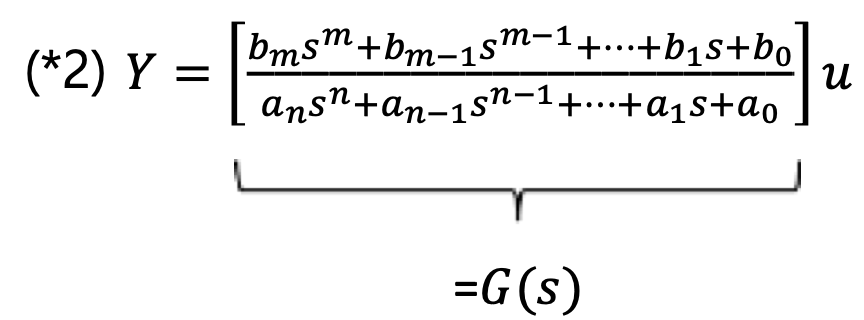시스템모델링제어 Chapter2. State-Space Models & Linearization
State-Space Model
- State Variables : Dynamic System 에서 상태변수는 최대한 적은 변수로 상태를 정의하는 것이다.
- State Space Model : 1차 미분방정식들의 모임으로 표현되는 n차 linear ODE
State Space Model 예시
y[3]+8y¨+9y˙+7y=u
Define
x1=yx2=y˙x3=y¨
Initial Condition
y(0)=y0y˙(0)=y0˙y¨(0)=y0¨
x1˙=x2x2˙=x3x3˙=−8x3−9x2−7x1+u
행렬로 변환
⎣⎢⎡x1˙x2˙x3˙⎦⎥⎤=⎣⎢⎡00−710−901−8⎦⎥⎤⎣⎢⎡x1x2x3⎦⎥⎤+⎣⎢⎡001⎦⎥⎤u
x 앞의 상수 행렬은 A행렬, u앞의 상수 행렬은 B행렬
y=[101]⎣⎢⎡x1x2x3⎦⎥⎤
x앞에 붙은 행렬은 C행렬
따라서 First-Order Differential Equation 은 다음과 같이 표현할 수 있다.
x˙=Ax+Buy=Cx
x(0)는 벡터 혹은 single valued 일 수 있다.
Generic nth-order ODE 는 다음과 같은 형태로 표현할 수 있다.
x˙(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)IC:x(0)=x0
- y(t) : 미래 output을 예상한 것 : 추정값
- x(t) : time = t 에서의 상태. input이 걸리는 동안의 모든 정보를 포함
→ State-Space Model 은 n차 미분방정식으로 표현 가능. n개의 서로 연결된 1차 미분방정식 집합체가 벡터로 표현 가능함.
State Space Model for RLC Circuit 예시
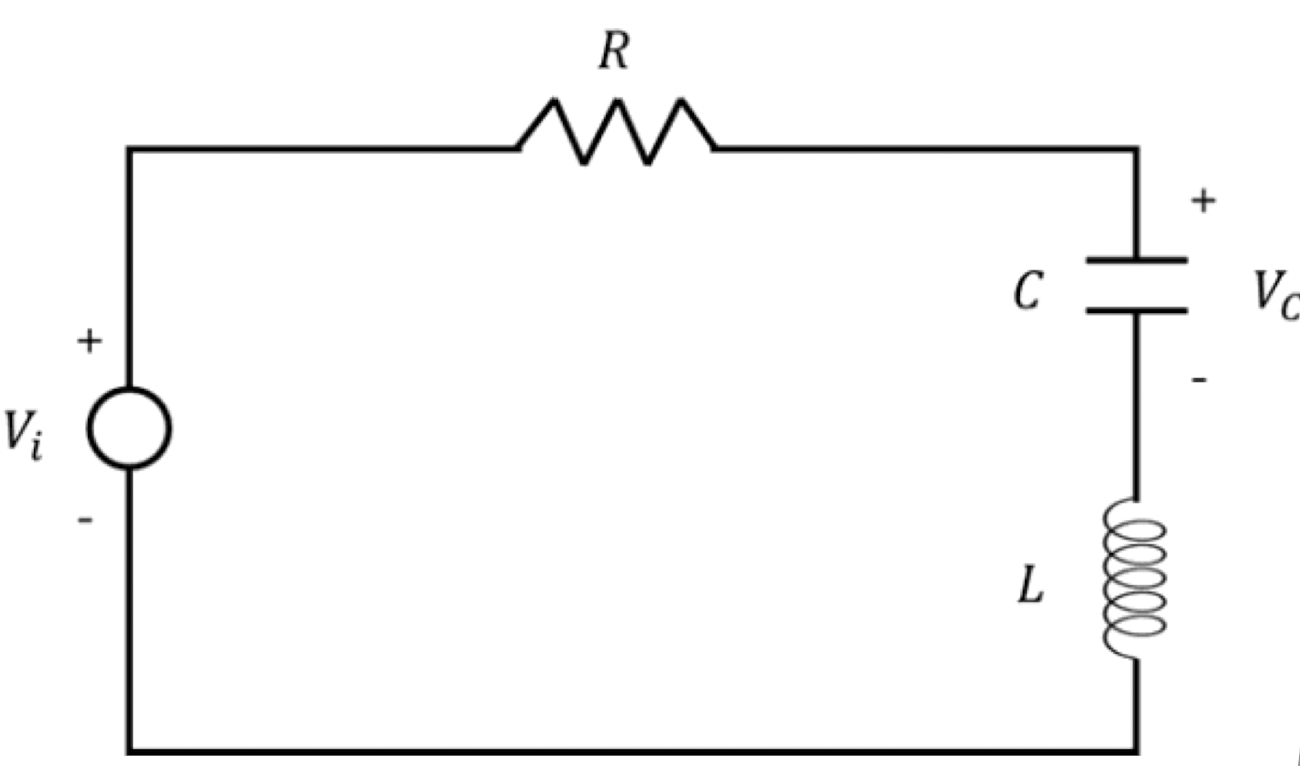
LCdt2d2Vc+RCdtdVc+Vc=Vi
dt2d2Vc+LRdtdVc+LC1Vc=LC1Vi
I.C={Vc(0)=Vc,0Vc˙(0)=ci0
Define
x1=Vcx2=Vc˙
x1˙=x2x2˙=Vc¨=−LRx2−LC1x1+LC1Vi
∴x˙=[x1˙x2˙]=[0−LC11−LR][x1x2]+[0LC1]Viy=[10][x1x2]
Nonlinear Mathematical Models
선형 ODE 모델로 만들 수 있는 비선형 모델을 배움. 대부분의 모델은 비선형 term을 가지고 있고, linearizing 또는 trimming 하여 단순화함.
single input을 가지는 n차 미분방정식의 state-space 모델을 다음과 같이 표현한다.
x˙=f(x,u)y=h(x,u)(i.c) x(0)=x0
Equilibrium Points
모든 상태 변수에 대하여 변화량이 없는 평형상태를 “Equilibrium Point”라고 한다.
f(xˉ,uˉ)=0
- x(0)=xˉ : system initialization
- u(t)=uˉ ∀t≥0
이때 solution x(t)는 다음을 만족하며 xˉ상태를 유지한다.
x(t)=xˉ ∀t≥0
Linearization
Non-linear System이 Equilibrium Point에 근접하게 작동한다면 선형 미분 방정식으로 예측이 가능하다! 이 과정에서 Jacobian Linearization 이 필요함.
Taylor Series Expansion
함수 f가 R→R 일 때, xˉ에 대하여 다음과 같이 표현할 수 있다.
f(x)≈f(xˉ)+dxdf(xˉ)⋅(x−xˉ)+HigherOrderTems
상태변수가 1개인 비선형 시스템은 다음과 같이 표현할 수 있다.
x˙=f(x,u) (*1)
Assumption (xˉ,uˉ) 는 equilibrium point 이다 : f(xˉ,uˉ)=0
- 이 시스템이 x(0)=xˉ 에서 시작하고
- input u(t)=uˉ ∀ t≥0 ⋯ (input이 바뀌지 X)
- (*1)의 솔루션은 x(t)=xˉ ∀t≥0 이다 ⋯ (초기조건에 머묾)
Question 만약 x(0)이 xˉ 에 근접하게 접근하고, 입력 u(t)가 uˉ에 근접하게 접근한다면?
sol1) (*1)을 그냥 풂 → 비선형 시스템이라 복잡함ㅠㅠ
sol2) 선형미분방정식을 유도한다! → 비선형 미분방정식 (*1)의 근사치를 제공함!!!
Conclusion
(xˉ,uˉ) 에 근접한 어떤 점에서 다변수(multi-variabl) 테일러급수를 통해 비선형함수의 근사치를 계산할 수 있다.
f(x,u)≈f(xˉ,uˉ)+dxdf(xˉ)⋅(x−xˉ)+dudf(uˉ)⋅(u−uˉ)
(뒤의 Higher Order Terms들은 복잡하므로 다 날림. 그럼에도 불구하고 근사치를 계산할 수 있다)
이 때, (xˉ,uˉ) 는 Equilibrium point 이므로 f(xˉ,uˉ)=0이다.
∴f(x,u)=dxdf(xˉ)⋅(x−xˉ)+dudf(uˉ)⋅(u−uˉ)
∴x˙=[dxdf(xˉ,uˉ)]⋅(x−xˉ)+[dudf(xˉ,uˉ)]⋅(u−uˉ) (*2)
따라서 (*)식을 다음과 같이 단순화시킬 수 있다.
A=dxdf(xˉ,uˉ)B=dudf(xˉ,uˉ)
δx(t)=x(t)−xˉδu(t)=u(t)−uˉ
dtd(δx(t))=δ˙x(t)=dtd(x(t)−xˉ)=x˙(t) ⋯ (*2) 에서 확장!
δ˙x(t)=x˙(t)=Aδx(t)+Bδu(t) (*3)
→ Linear State-Space Model : 선형 상태공간 모델
3은 비선형 방정식 (1)을 근사 예측할 수 있게 한다. 단, (xˉ,uˉ)에 근접해야한다는 조건이 있음
x(t)는 x(0)에서 시작되고 input(u)를 가지는 비선형모델 (*1)의 솔루션이다.
δx(t)는 δx(0)=x(0)−xˉ에서 시작하고 input δu(t)=u(t)−uˉ를 가지는 선형모델인 (*3)의 솔루션이다.
Linear Solution은 Non-Linear Solution을 근사화해준다. 단, Equilibrium point 의 작은 오차범위에서 유효하다.
x(t)≈xˉ+δx(t)
Generalization
n-state System일 때 Linear State Model을 얻기 위해 일반화함!
output equation을 다음과 같이 쓸 때 output 또한 linearization 가능함.
x˙=f(x,u)y=h(x,u)
yˉ=h(xˉ,uˉ) 일때 δy(t)=y(t)−yˉ 이라고 하면, equilibrium output은 다음과 같이 근사화된다.
δy(t)≈[▽xh(xˉ,uˉ)]δx(t)+[▽uh(xˉ,uˉ)]δu(t)
C=[▽xh(xˉ,uˉ)]D=[▽uh(xˉ,uˉ)]
∴δ˙x(t)=Aδx(t)+Bδu(t) δy(t)=Cδx(t)+Dδu(t)
Transfer Function
n차 선형미분방정식을 Laplace Transform 을 이용하여 표현할 수 있다.
전달함수 G(s)는 선형미분방정식과 관련된 전달함수이며 미분방정식을 다르게 표현한 것이다.
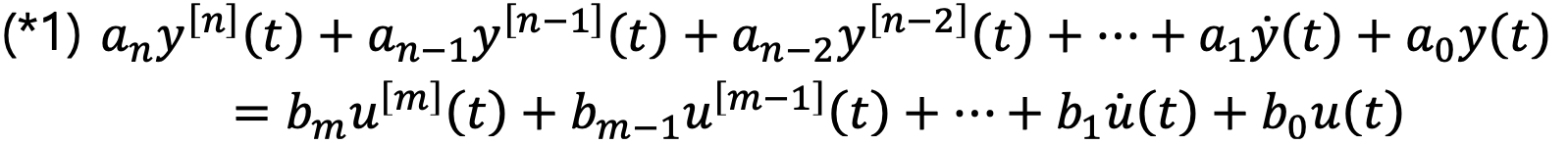
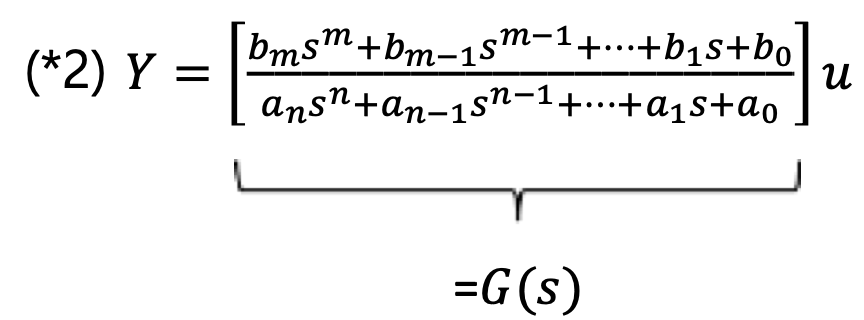
예시) 6y¨+9y˙+2y=4u˙+8u
G(s)=6s2+9s+24s+8
Summary
Nonlinear ODE —(Jacobian : Linearization) —> Linear ODE —(Laplace Transform) —> Transfer Function
- Nonlinear ODE 는 Equilibrium Point 에 근접할 때 선형미분방정식으로 근사치를 예상할 수 있다.