시스템모델링제어 : Open-Loop와 Closed-Loop Control

시스템모델링제어 Chapter4. Open-Loop Control

First Order System 을 base로 open-loop vs closed loop 제어성능 비교!

전체적으로 예시를 가지고 설명!

Open-Loop Control

DC모터 Inertia J. output x(t) 는 샤프트 각속도(rad/sec), input u(t)는 volage(V). 단, eletro-mechanical System의 도메인 특성을 다음과 같이 설정하여 가정함.
1) 전기적인 신호는 굉장히 빠름 → step response
2) Voltage v(t)는 모터토크에 바로 반영됨!
Ku(t) = Torque … shaft에서!
3) shaft bearing에는 마찰이 존재함. - cx(t)

$J\dot{x} = Ku(t) - cx(t)$

$Assum = \begin{cases} J = 2kg \cdot m^2 \\ K = 4 \frac{N\cdot m}{v} \\ c = 10N \cdot m \cdot sec \end{cases}$

$⇒ 2\dot{x} + 10x = 4u\\ x(0) = 0$

Step Normalize

$\begin{cases} \dot{x} + 5x = 2u \\ x(0) = x_0 \end{cases}$

⇒ a = 5 > 0 → system is stable!

Design Objective

• “r” 을 “desired reference command” 라고 한다. → 여기서는 샤프트 속도!
• voltage u(t)를 입력하였을 때 실제 모터 샤프트 속도가 desired speed r에 수렴하는 지 확인해야함
• desired speed x(t)는 r에 수렴할 것임. r은 상수이다!

Step Response

$x(t) = \frac{b}{a}(1-e^{-at})u_0$

$\therefore x(t) = \frac{2}{5}(1-e^{-5t})u_0$

이 시스템이 Steady-State 에 도달한다고 할 때($t→\infin$), $\dot{x} = 0$이다.

$⇒ x_{ss} = \frac{b}{a}u_0 = \frac{2}{5}u_0$

Conclusion

Step Response에서 $x(t) → \frac{b}{a}u_0 = \frac{2}{5}u_0$ 에 수렴함. Design Object는 x(t)→r 하기 위한 V(t)를 찾아내는 것이다!

$\therefore u_0 = \frac{5}{2}r$ 해당하는 다이어그램은 다음과 같다.

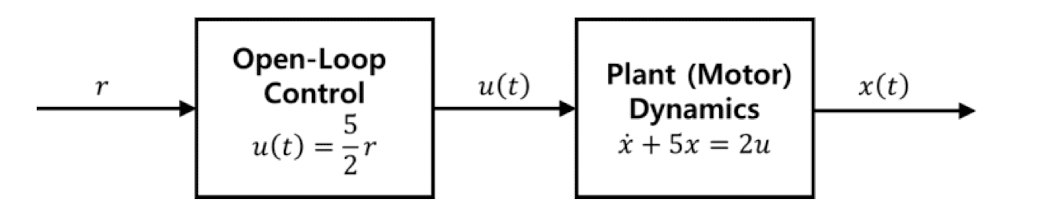
각각 r=1,2,3일 때의 그래프이다. 같은 비율로 수렴하는 이유는 r만 다르고 T는 같기 때문이다. 3T에 95% 성능을 달성한다.

Open-Loop Disturbance Rejection

Real World 에서는 Wind Gust, Road Slope, Additional Load Torque 등의 disturbance가 있음.

Disturbance를 고려함으로써 설계한 제어기가 외란의 영향을 최소화할 수 있음.

Simple Disturbance 모델은 다음과 같다.

$\dot{x} + Ax = B(u+d)$

$d(t) = \bar{d} \ \ \ \ \forall t≥0$ 이고 system이 stable 하여 steady-state에 수렴한다고 할 때, steady-state value x(t)는 다음과 같이 쓸 수 있다(예제 연결)

$\dot{x} + 5x_{ss} = 2(u + \bar{d}) \\ \therefore x_{ss} = r + \frac{2}{5}\bar{d}$

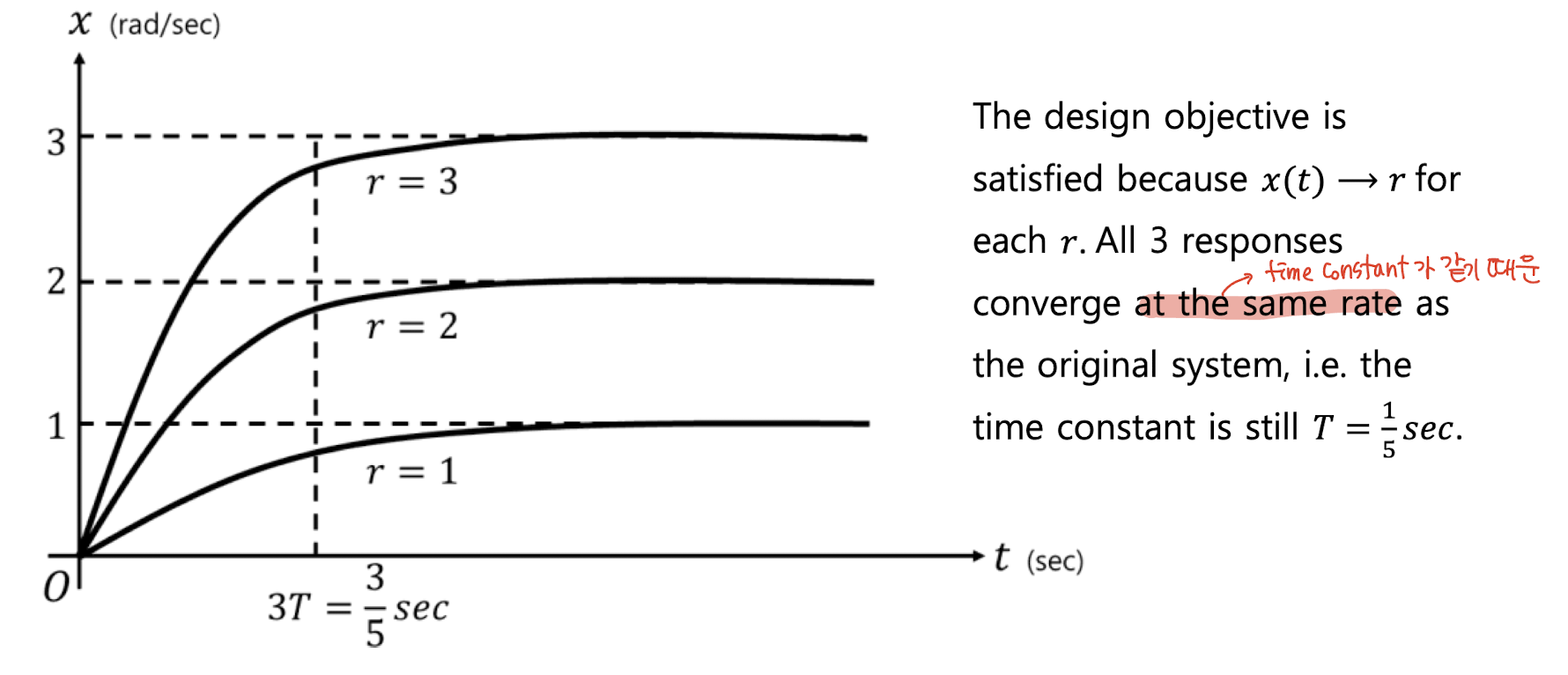
r = 1 로 고정하고 $\bar{d}$=0,1,2라고 할 때 그래프는 다음과 같이 그려짐

$\bar{x} = 1$ 일 때 $x_{ss} = 1.4 → steady-state error e_{ss} = x_{ss}-r = 0.4$

Proportional Control

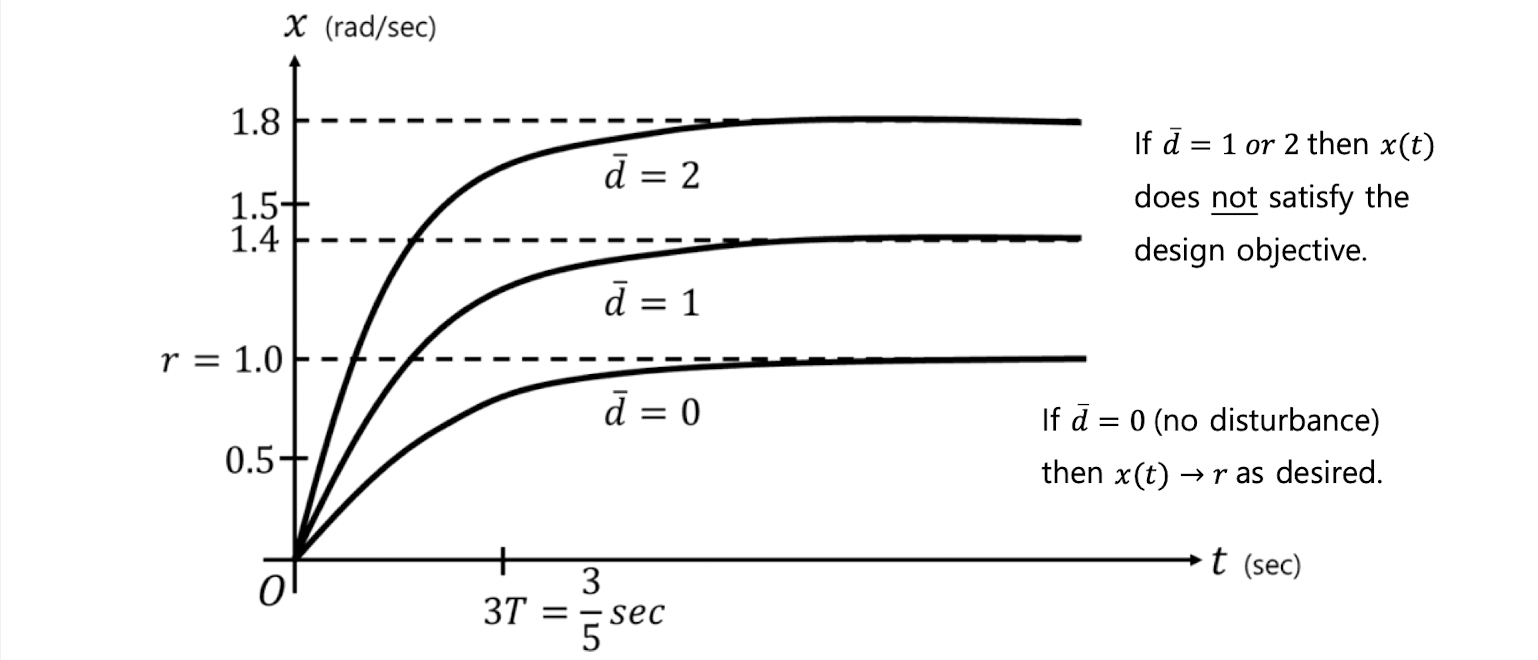
간단한 closed-loop control strategy는 다음과 같이 input을 설정할 수 있음!

$u(t) = K_p(r-x(t))$

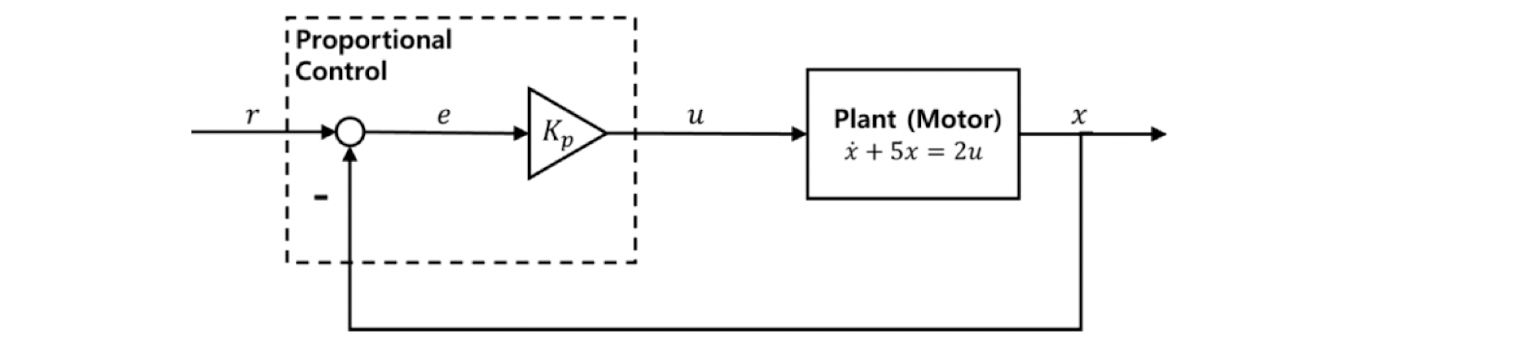
output x가 e에 영향을 줌 → e가 input u에 영향을 줌 → input u가 output x에 영향을 줌 → 반복…

⇒ Closed-Loop Control!

(예제 연결 적용)

$\dot{x} + 5x_{ss} = 2u \\ u = K_p(r-x(t)) \\ \therefore \dot{x} + 5x = 2Kp(r-x)$

⇒ $\dot{x} + (5 + 2K_p)x = 2K_pr$

System Things Check

Time-Constant T

$T = \frac{1}{a} = \frac{1}{5+2K_p}$

→ $K_p$ 값으로 응답성을 바꿀 수 있으며, $K_p$를 올리면 응답성이 올라가서 빠르게 r에 수렴함

Steady-State Value$x_{ss}$

$(5 + 2K_p)x_{ss} = 2K_pr$

$\therefore x_{ss} = \frac{2K_p}{(5 + 2K_p)}r = \frac{1}{1+\frac{5}{2K_p}}r \\ e_{ss} = r-x_{ss} = r-\frac{1}{1+\frac{5}{2K_p}}r = \frac{2K_p}{2K_p+5}r$

→ $K_p$를 적당히 올림으로써 $e_{ss}$를 줄일 수 있음!

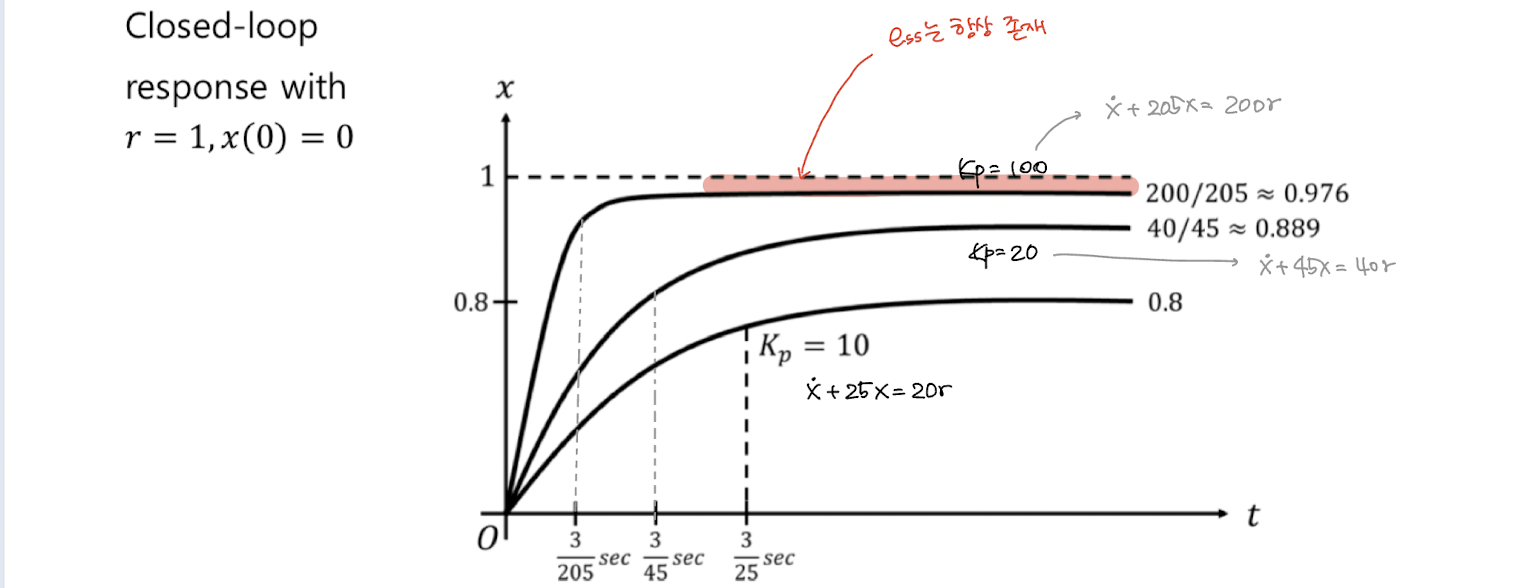
Open-Loop 와 비교

• response time이 빨라짐! → $K_p$
• $e_{ss}$를 줄일 수는 있지만 항상 존재함.

Proportional Control Disturbance Rejection

Open-Loop & Closed-Loop 의 Disturbance Rejection을 비교해보자!

$\dot{x} + 5x = 2(u + d) \\ u = K_p(r-x(t))$

$\therefore \dot{x} + 5x = 2d + 2K_p(r-x) \\ \dot{x} + (5 + 2K_p)x = 2K_pr + 2d$

disturbance $d(t)=\bar{d} \ \ \ \ \forall t≥0$ 일 때 steady-state value와 그 그래프는 다음과 같다.

$x_{ss} = \frac{2K_p}{5+2K_p}r + \frac{2}{5 + 2K_p}\bar{d}$

→ $K_p$를 높임으로써 disturbance 영향을 줄일 수 있음!

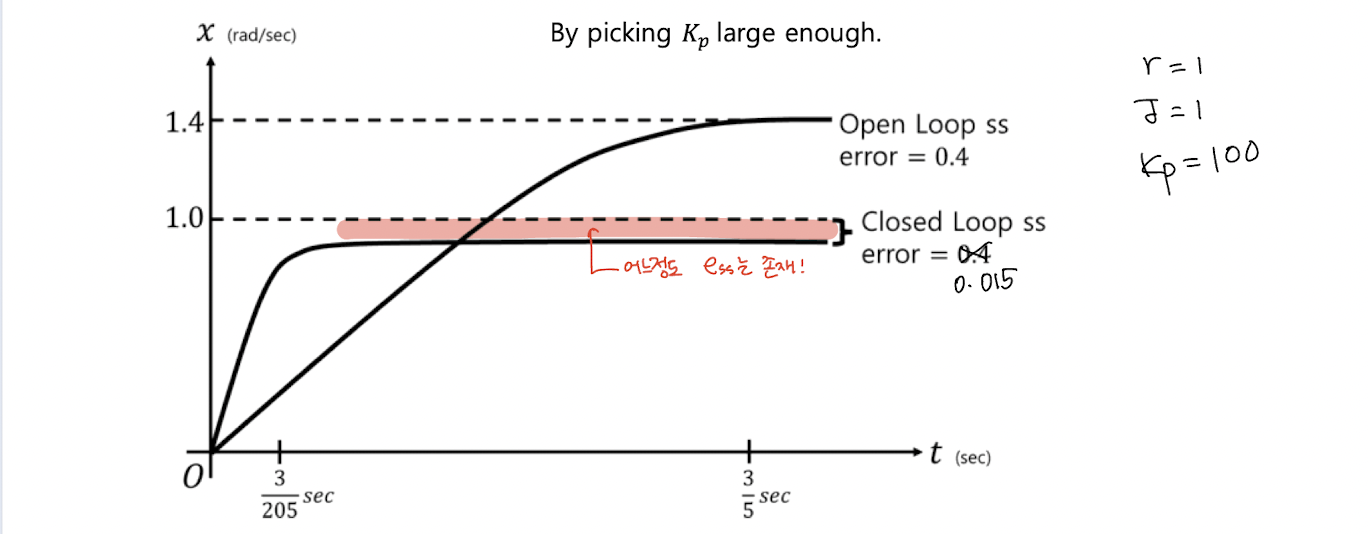
FeedForward Control

Open-loop와 P Control 을 접목시킨 제어방법.

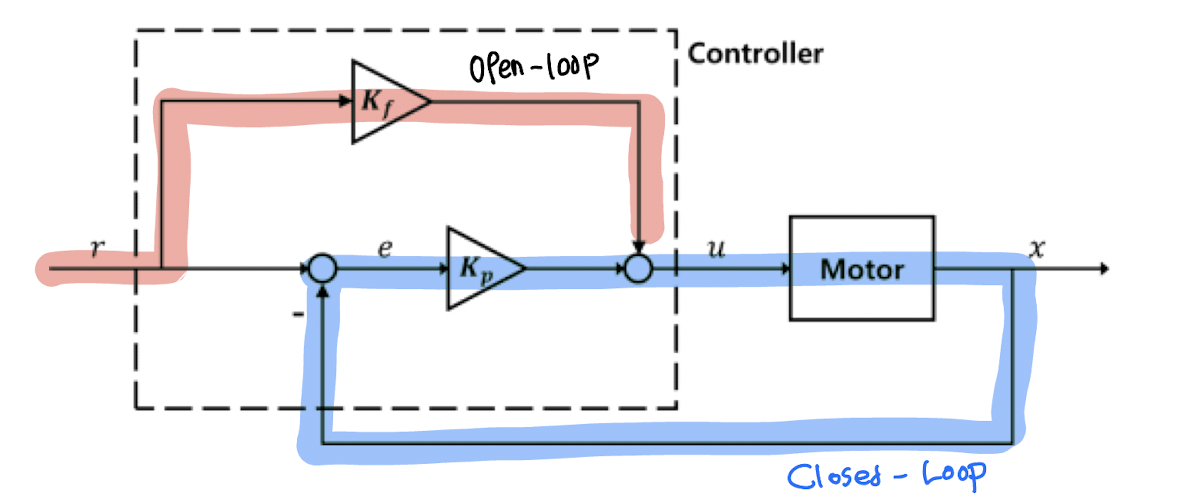
(예제 연결하여 설명)

$\dot{x} + 5x = 2u \\ u = K_p(r-x(t)) + K_fr \\ \therefore \dot{x} + 5x = 2K_p(r-x) + 2K_fr \\ \dot{x} + (5+2K_p)x = 2(K_p+K_f)r$

Time-Constant T

$T = \frac{1}{5+2K_p}$

Steady-State Error$E_{ss}$

$(5+2K_p)x_{ss} = 2(K_p+K_f)r$

$x_{ss} = \frac{2(K_p + K_f)}{5+2K_p}r$

$e_{ss} = r-x_{ss} = \frac{2-2K_f}{5+2K_p}r$

→설계자가 선택한 $K_p$, $K_f$로 $x_{ss}$ 설정 가능함.

$K_p$는 $T$, $K_f$는 $e_{ss}$ 와 연관성이 높음

단, FeedForward Control은 Disturbance Rejection과 연관성은 적음.