시스템모델링제어 : 1차시스템

시스템모델링제어 Chapter3. First Order System

Introduction & General Solution

→ 이번 챕터에서는 1차 선형시스템과 General Solution, Free Response, Step Response만 다룸.

Impulse, Sinusoidal Response 는 진동학에서 다룸.

Input의 타입에 따라 솔루션을 설명할 수 있다.

Background Concept

• Stability : 안정성
• Time Constant : 시스템의 응답이 얼마나 따른지를 나타내는 척도
• Steady-State Value\

General Solution

초기 상태 $x(0) = x_0$ 와 임의의 input function u(t) 가 t≥0 에 대하여 주어질 때 1차 ODE를 다음과 같이 쓰고 솔루션을 구할 수 있다.

$\begin{cases} \dot{x} + ax = bu \\ x(0) = x_0 \end{cases}$ (*1)

$x(t) = e^{-at}x_0 + \int_0^t e^{-a(t-\tau)}bu(\tau)d\tau$ (*2)

앞부분은 Free Response(=I.C Response), 뒤에 적분 부분은 Forced Response

Free Response & Time Constant

(=Inital Condition Response)

1차 ODE에서 $u(t) = 0 \ \ (\forall t≥0)$ 일때 forced response가 없으므로 다음과 같이 솔루션을 쓸 수 있음.

$x(t) = e^{-at}x_0$

이 때 solution의 특성은 a에 의하여 결정됨.

time constant T = $\frac{1}{a}$

이론적으로 3T(sec)에서 시스템의 95% 성능을 달성함.

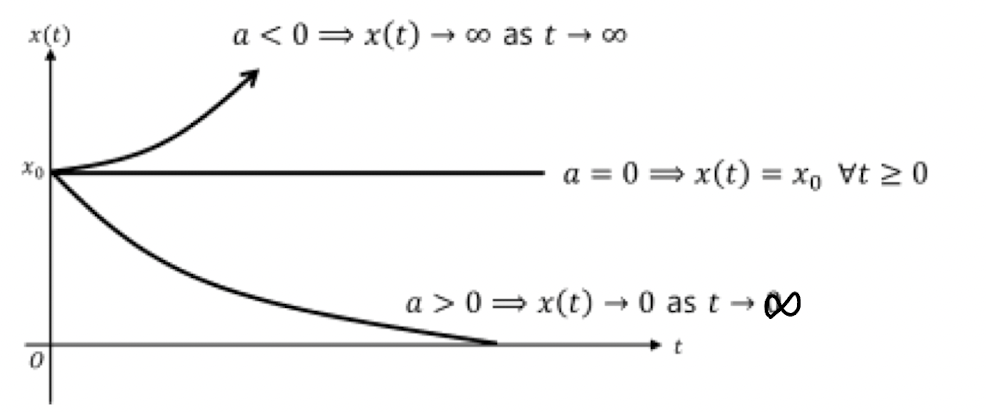
• a > 0 : Free response는 stable함
• a = 0 : Free Response는 marginally stable함
• a < 0 : Free Response는 unstable함 → 논리적으로, 시스템이 음수sec에 시스템의 95%를 달성할 수 없음!

Step Response

step input은 다음과 같은 성격을 가진다.

$u(t) =\begin{cases} 0 (t<0) \\ u_0 (t≥0) \end{cases}$

이 때 $u_0$는 상수이다. general solution을 이용하여 퍼포먼스를 보여줄 수 있다.

$x(t) = e^{-at}x_0 + \int_0^t e^{-a(t-\tau)}bu(\tau)d\tau$

$a>0$일 때 솔루션은 다음과 같이 일반화할 수 있다.

$x(t) = e^{-at}x_0 + \frac{b}{a}(1-e^{-at})u_0$

$a>0$일 때 $t→\infin$하면(steady-state) $x(t) → \frac{b}{a}u_0$ 이다. 이 때 time constant $T = \frac{1}{a}$ 이며, 3T(sec)일 때 시스템의 95% 성능을 낼 수 있다!

+) a = 0 case

이 때 만약 a=0 이면 $x(t) = x_0 + bu_0\cdot t$ 이다. 이때 $t→\infin$ 하면(steady-state) x(t)값은 무한대로 증가하므로 stable할 수 없다.

+) a < 0 case

이 때 만약 a<0이면 $x(t)→-\frac{b}{a}e^{-at}$ 이고 $t→\infin$ 하면 x(t)값이 무한대로 exponentially 무한대로 증가하므로 stable 할 수 없다.

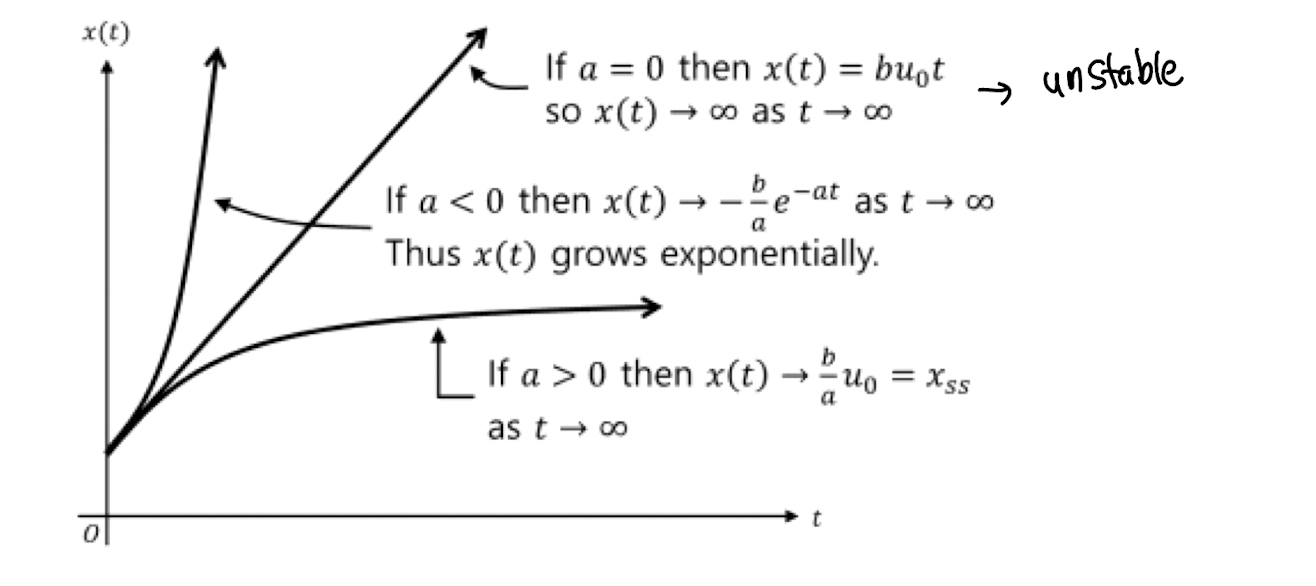
Concept : BIBO

Bounded Input-Bounded Output : stable을 구분하는 척도 (time constant는 반응성의 척도임)

Bounded : 어떤 신호 x(t)가 정해진 A보다 작음

$|x(t)| < A <\infin \ \ \ \ (\forall$ $t≥0)$

만약 어떤 input u(t)가 bounded 하다고 할 때 다음을 만족함.

• 어떤 수 N에 대하여 $|u(t)| < N \ \ \ \ (\forall t≥0)$
• 어떤 수 M에 대하여 $|x(t)| < M \ \ \ \ (\forall t≥0)$

→ input u(t), output x(t) 모두 bounded 하다.

⇒ $a≤0, x(t) →\infin$ 일때 1차 선형시스템은 not BIBO stable하다.
$a>0, x(t) → X_{ss}$일 때 BIBO stable 하다.