🌠"캐슬 디펜스" - 17135번 G4

🎃문제설명
🏰캐슬 디펜스는 성을 향해 몰려오는 적을 잡는 턴 방식의 게임이다. 게임이 진행되는 곳은 크기가 N×M인 격자판으로 나타낼 수 있다. 격자판은 1×1 크기의 칸으로 나누어져 있고, 각 칸에 포함된 적의 수는 최대 하나이다. 격자판의 N번행의 바로 아래(N+1번 행)의 모든 칸에는 성이 있다.
성을 적에게서 지키기 위해 궁수 3명을 배치하려고 한다. 궁수는 성이 있는 칸에 배치할 수 있고, 하나의 칸에는 최대 1명의 궁수만 있을 수 있다. 각각의 턴마다 궁수는 적 하나를 공격할 수 있고, 모든 궁수는 동시에 공격한다. 궁수가 공격하는 적은 거리가 D이하인 적 중에서 가장 가까운 적이고, 그러한 적이 여럿일 경우에는 가장 왼쪽에 있는 적을 공격한다. 같은 적이 여러 궁수에게 공격당할 수 있다. 공격받은 적은 게임에서 제외된다. 궁수의 공격이 끝나면, 적이 이동한다. 적은 아래로 한 칸 이동하며, 성이 있는 칸으로 이동한 경우에는 게임에서 제외된다. 모든 적이 격자판에서 제외되면 게임이 끝난다.
게임 설명에서 보다시피 궁수를 배치한 이후의 게임 진행은 정해져있다. 따라서, 이 게임은 궁수의 위치가 중요하다. 격자판의 상태가 주어졌을 때, 궁수의 공격으로 제거할 수 있는 적의 최대 수를 계산해보자.
격자판의 두 위치 (r1, c1), (r2, c2)의 거리는 |r1-r2| + |c1-c2|이다.
입력
첫째 줄에 격자판 행의 수 N, 열의 수 M, 궁수의 공격 거리 제한 D가 주어진다. 둘째 줄부터 N개의 줄에는 격자판의 상태가 주어진다. 0은 빈 칸, 1은 적이 있는 칸이다.
출력
첫째 줄에 궁수의 공격으로 제거할 수 있는 적의 최대 수를 출력한다.
🔒제한사항
- 3 ≤ N, M ≤ 15
- 1 ≤ D ≤ 10
💾입출력 예
| 입력 | 출력 |
|---|---|
| 5 5 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 | 3 |
| 5 5 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 | 3 |
| 5 5 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 | 5 |
| 5 5 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 | 15 |
| 6 5 1 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 0 | 9 |
| 6 5 2 1 0 1 0 1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 0 | 14 |
알고리즘 분류
- 구현
- 그래프 이론
- 브루트포스 알고리즘
- 시뮬레이션
강의내용
🌟문제 이해 및 풀이계획
✏️처음에는 문제가 잘 이해가 안됐다. 가장 왼쪽에 있는 적을 공격하며 가장 최대의 적을 공격하는 횟수를 구해야 하는데, 왼쪽의 기준이 위,아래,왼,오 에서 우선순위를 어떤식으로 정해야 하는지 헷깔렸다. (사실 문제를 제대로 꼼꼼하게 읽지 않아서 인 것 같다..ㅠ)
✏️각 턴당 모든 궁수(3명)은 동시에 적 1명만 공격이 가능하고, 적은 중복으로 공격이 가능하다.
✏️가장 가까운 적부터 공격이 가능하고, 같은 거리의 적들은 가장 왼쪽부터 공격이 가능하다.
✍🏻내 코드1 - 오답코드
코드를 입력하세요❌처음에는 문제의 규칙을 꼼꼼하게 이해하지 못해서 중복 공격에 대한 가능성을 고려하지 않았고, 거리를 고려하지 않고 무조건 궁수기준 왼쪽의 적을 공격하게 했다.
❌그래서 격자판의 적 기준으로 궁수를 선택했는데 궁수 기준으로 코드를 다시 짜야겠다고 생각했다.
✍🏻내 코드2 - 정답코드
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static int n, m, d, max = 0;
static int[] archer = new int[3]; // 궁수 위치
static int[][] grid;
static int number = 0;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
d = sc.nextInt(); // 궁수 공격 제한거리
grid = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
grid[i][j] = sc.nextInt();
}
}
sc.close();
archer(m, 3, 0);
System.out.println(max);
}
// 궁수 배치
public static void archer(int nn, int r, int start) {
if (r == 0) {
int[][] grid_copy = new int[n][m];
for (int i = 0; i < n; i++) {
System.arraycopy(grid[i], 0, grid_copy[i], 0, m);
}
max = Math.max(max, attack(archer, grid_copy));
return;
}
for (int i = start; i < nn; i++) {
archer[3 - r] = i;
archer(nn, r - 1, i + 1);
}
}
// 적 공격
public static int attack(int[] archer, int[][] grid_copy) {
int num = 0; // 공격 횟수
boolean[] archer_v = new boolean[3];
// 가장 왼쪽 적부터 공격, 궁수 기준
for(int k=0; k<3; k++) { // 궁수
if (!archer_v[k]) {
loop:
for(int i=1; i<=d; i++) {
for(int j=-i+1; j<=i-1; j++) {
int x = -(i - Math.abs(j));
if (n + x >= 0 && n + x < n && archer[k] + j >= 0 && archer[k] + j < m) {
if (grid_copy[n + x][archer[k] + j] == 1) {
grid_copy[n + x][archer[k] + j] = -1; // 적 소멸
num += 1;
break loop;
}
if (grid_copy[n + x][archer[k] + j] == -1) { // 중복 공격
break loop;
}
}
}
}
}
if (k == 2) {
if (move(grid_copy) == 0)
break; // 적이 없을 때 스톱
k = -1; // 다시 처음부터
Arrays.fill(archer_v, false);
}
}
return num;
}
// 턴 종료 후 적 이동
public static int move(int[][] grid_copy) {
int enemy = 0;
Arrays.fill(grid_copy[n - 1], 0); // 마지막 행 0으로 채우기
for (int i = n - 2; i >= 0; i--) {
for (int j = 0; j < m; j++) {
if(grid_copy[i][j] == -1) grid_copy[i][j] = 0;
if(grid_copy[i][j] == 1) {
grid_copy[i][j] = 0;
grid_copy[i + 1][j] = 1; // 적 아래로 이동
enemy += 1;
}
}
}
return enemy;
}
}✔️궁수를 기준으로 모든 적이 사라질 때까지 각 턴마다 for문을 돌려 각 궁수가 공격하는 적을 구한다.
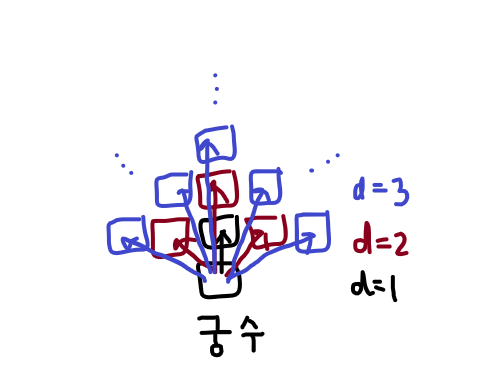
✔️위 그림처럼 공격 가능한 거리 d를 1부터 모두 고려하려 가장 가까운 1부터 d까지 왼쪽부터 적이 있는지 모두 확인한다.
-
d = 1
(n, 궁수위치) + (-1, 0) -
d = 2
(n, 궁수위치) + (-1, -1)
(n, 궁수위치) + (-1, 0) -
d = 3
(n, 궁수위치) + (-1, -2)
(n, 궁수위치) + (-2, -1)
(n, 궁수위치) + (-3, 0)
(n, 궁수위치) + (-2, 1)
(n, 궁수위치) + (-1, 2)
...
✔️궁수 기준으로 공격할 위치를 탐색할 때 현재 궁수 위치에서 거리*2-1수 만큼 탐색하고 위의 규칙에 따라 for문을 돌려서 1 또는 -1(앞선 궁수가 공격한 적)일 때 -1로 만들어주고 공격수를 +1한다.
✔️모든 궁수가 공격한 후 턴 종료를 위해 격자판을 한 줄씩 앞당기고 이 때, 적이 없으면 최종 공격값을 리턴한다.
💡attack함수의 코드가 많이 복잡한데 좀 더 간단하게 풀 수 있는 방법을 고민해봐야겠다.
💡문제에 대한 정확한 규칙을 꼼꼼히 파악하지 못해 오래걸린 문제였다. 제한사항을 꼼꼼하게 파악하고 그 속에서 최대한 규칙을 찾아 구현하는데 익숙해져야겠다..


