📖 학습한 내용
- 약수와 소수
- 소인수와 소인수분해
- 최대공약수
- 최소공배수
- 진법
- 등차 수열
- 등비 수열
- 시그마
- 계차수열
- 피보나치 수열
📖 핵심내용
📌 약수와 소수
약수 : 어떤 수를 나누어 떨어지게 하는 수
소수 : 1과 자기 자신만으로 나눠지는 수
소수의 반대말은 합성수이다.
- 소수 찾기 코드
inputNumber = int(input("0보다 큰 정수 입력: "))
for number in range(2, (inputNumber + 1)):
flag = True
for n in range(2, number):
if number % n == 0:
flag = False
break📌 소인수와 소인수분해
소인수 : 소수이면서 인수(약수)인 수
소인수분해 : 1제외 소인수의 곱으로 나타낸것
# 소인수 찾아내기
inputNumber = 10
n = 2
while n <= inputNumber:
if inputNumber % n == 0:
print('소인수: {}'.format(n))
inputNumber /= n
else:
n += 1📌 최대공약수
두개 이상의 수에서 공통된 약수를 공약수라고 한다.
최대 공약수의 약수가 공약수이다.
# 최대 공약수 찾기
# 2개 동시에 나눴을때 둘다 나눠지는 최대의수
#num1 < num2
num1 = 12
num2 = 30
maxNum = 0
for i in range(1, num1+1):
if num1 % i == 0 and num2 % i ==0:
maxNum = i
print(maxNum)📌 최소공배수
공통된 배수에서 가장 작은수
두수의 곱을 두수의 최대공약수로 나누면 최소공배수가 된다.
3개의 수의 최소공배수를 구하려면, 먼저 두수의 최소공배수를 구하고, 나온 최소공배수와 나머지 남은 수의 최소공배수를 구한다. 그렇게 나온 것이 세 수의 최소공배수이다.
#num1 < num2
num1 = 12
num2 = 30
maxNum = 0
for i in range(1, num1+1):
if num1 % i == 0 and num2 % i ==0:
maxNum = i
minNum = num1 * num2 // maxNum # 두수의 곱을 최대공약수로 나누면 최소공배수가 나온다.📌 진법
자리수를 구분하는 최소단위가 진수이다.
- 진법 변환 :
bin(),oct(),hex()
# 10진수 -> X진수
print('2진수: {}'.format(bin(dNum)))
print('8진수: {}'.format(oct(dNum)))
print('16진수: {}'.format(hex(dNum)))-> 10진수를 다양한 진수로 변환한 값은 모두 문자열이다.
다양한 진법 변환은 tip에 적어두고 필요할때 찾아보면서 익숙해질 것이다.
📌 수열
규칙성을 가지고 나열된 수들
일반항 - n번째 항을 문자로 표기한 것
등차 수열
-
연속된 두항의 차이(공차)가 일정한 수열
-
일반항

-
등차 중항
연속된 세항에서 가운데 항 -
수열의 합
규칙성을 이용해서 모든 항들의 총합을 구할 수 있다.
등차 중항을 이용하여 식을 단순화한다.
수열(합) 공식: sn = n(a1 + an) / 2
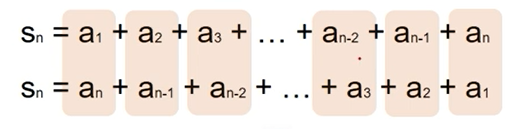
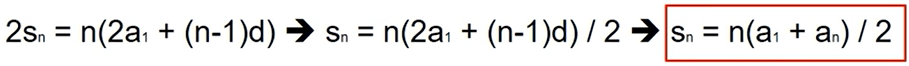
-
등차수열 코드
inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))
# 공식을 이용. 공식몰라도 충분히 추론 가능
valueN = inputN1 + (inputN-1) * inputD
print('{}번째 항의 값: {}'.format(inputN, valueN))- 등차수열의 합 코드
inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))
# 공식을 이용. 공식몰라도 충분히 추론 가능
valueN = inputN1 + (inputN-1) * inputD
sumN = inputN * (inputN1 + valueN) / 2
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))등비 수열
연속된 두 항의 비(공비)가 일정한 수열
등비 수열 규칙성을 이용해서 일반항을 구할 수 있다.
등비 수열(일반항) 공식: an = a1 * r^(n-1)

-
등비 중항
연속된 세항에서 가운데항 -
등비 수열의 합
등비 수열(일반항) 공식: an = a1 * r^(n-1)
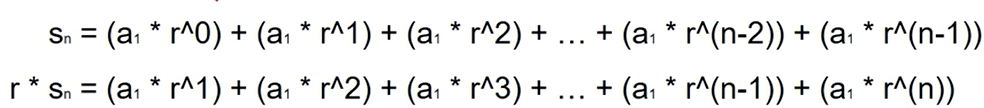
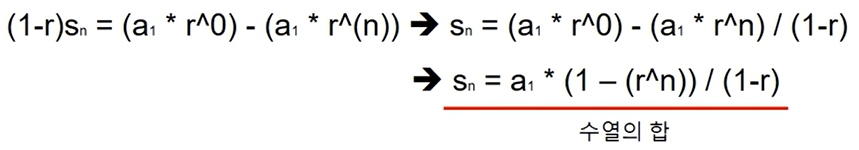
-
등비수열 코드
inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))
# 공식을 이용. 공식몰라도 충분히 추론 가능
valueN = inputN1 * (inputR ** (inputN-1))
print('{}번째 항의 값: {}'.format(inputN, valueN))- 등비수열의 합 코드
inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))
# 공식을 이용. 공식몰라도 충분히 추론 가능
valueN = inputN1 * (inputR ** (inputN-1))
print('{}번째 항의 값: {}'.format(inputN, valueN))📌 시그마
수열의 합을 나타내는 기호
앞에서 등비수열/등차수열의 합을 표기함
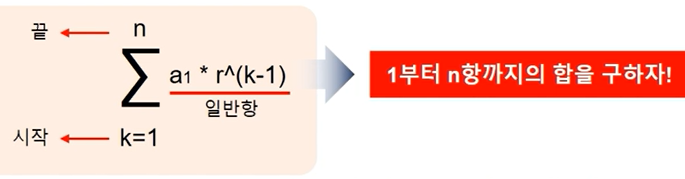
📌 계차수열
어떤 수열의 인접하는 두 항의 차로 이워진 또 다른 수열
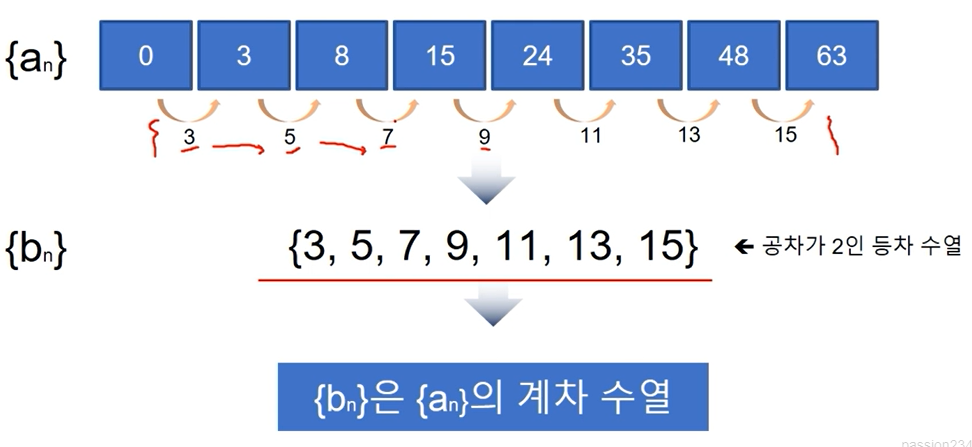
-> bn은 an의 계차수열이다.
- 계차수열 일반항

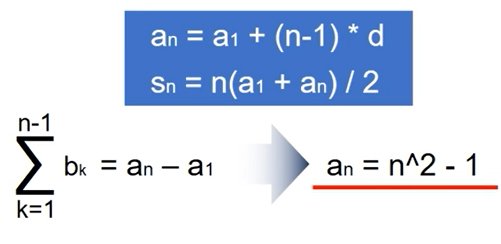
->b은 등차수열이므로 등차수열 일반항과 합의 공식을 쓸 수있다. 따라서 등차수열 b의 1에서 (n-1)까지의 합을 구할 수 있다. 이것을 구했다면 a수열의 일반항을 구할 수 있다.
📌 피보나치 수열
세번째 항은 두번째 항과 첫번째 항을 더한 값이다.
- 피보나치 수열 코드로 구현
1번과 2번항에 값을 주고 이후 전달과 전전달의 합을 구하려는 항에 준다.
while n <= inputN:
if n == 1 or n == 2:
valueN = 1
valuePreN2 = valueN
valuePreN1 = valueN
sumN += valueN
n += 1
else:
valueN = valuePreN2 + valuePreN1
valuePreN2 = valuePreN1 # 전전달에 전달 값주기
valuePreN1 = valueN # 전달에 이번달 값주기
sumN += valueN # 항들의 총합 구하기
n += 1📖 흥미로운 점 / 새로 알게된 점
-
어떤 값(n)이 소수인지 판별하는 코드 핵심 아이디어는, 1과 값(n) 사이의 수의 나머지가 0인지 아닌지로 판단하넌 것이다. 그리고 for문 도중 소수인게 한번이라도 걸린다면,
flag=False로 주고 반복문을 나와서 소수인지 아닌지 판단하는 아이디어가 있다. -
최대공약수 찾는 핵심 아이디어
num1 % i == 0 and num2 % i ==0과, for문에서 반복 범위(range안의값)가 두 수중 작은 수로 반복해야하는 당연한 사실을 잊지말자.
num1 = 12
num2 = 30
maxNum = 0
for i in range(1, num1+1): # range() 안에 둘 중 작은수(num1)가 들어가야함
if num1 % i == 0 and num2 % i ==0:
maxNum = i
print(maxNum)-
최소공배수는 두 수의 곱을, 두 수의 최대공약수로 나눈 값을 알면 코드로 구현하기 매우 쉽다.
-
진법에서의 코드는 적어두고 필요할때 찾아보며 눈에 익혀두는 것이 좋을 것 같다.
-
등차수열과 등차수열의 합, 등비수열과 등비수열의 합에서, 첫번째 항을 따로 계산해줘야한다는 아이디어를 잊지말자. 또한 첫항에서도 while 문이기 때문에
n+=1을 해줘야한다. -
등차수열b의 합은 n-1까지 합을 구해야하는 것을 주의하자.
📖 이후 학습 계획
- 팩토리얼
- 군 수열
- 순열
- 조합
- 확률
- 기초수학 연습문제