📖 학습한 내용

• 팩토리얼
• 군 수열
• 순열
• 조합
• 확률

📖 핵심내용

📌 팩토리얼

1부터 양의 정수 n까지의 정수를 모두 곱한 것
0! = 1 로 약속

• 코드로 팩토리얼 표현

  inputN = int(input('n 입력: '))
  result = 1
  for n in range(1, inputN+1):
      result *= n
  print('{} 팩토리얼: {}'.format(inputN, result))

📌 군 수열

여러개의 항을 묶었을 때 규칙성을 가지는 수열

-> 묶은 군의 숫자가 공차가 1인 등차수열이다.
-> 따라서 등차수열의 합을 이용하면 타겟항의 개수가 몇개인지 예측할 수 있다.
-> 또한 타겟 항이 속한 군이 몇까지 진행하는지 알 수 있다.
-> 이를 이용해 타겟 항 군의 전번 군이 몇으로 끝나는지 알아낸 뒤, 규칙성을 이용해 타겟 항의 값을 알아낼 수 있다.

while문을 사용해서 전체 항이 진행되게하고, for문을 이용해서 군이 진행되게한다.

📌 순열 permutation

n개에서 r개를 택하여 나열하는 경우의 수
순서가 다르면 다른 경우이다.

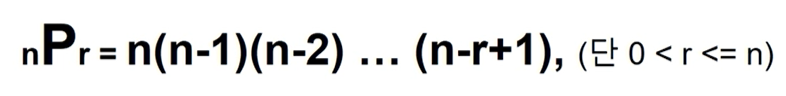
n!/(n-r)! 또는 n(n-1)(n-1)...(n-r+1) -> range(n, n-r, 01)

원순열

시작과 끝의 구분이 없는 순열
n!/n 또는 (n-1)! -> range(1,n)

📌 조합 permutation

순서와 상관없이 r개 택하는 것
n개에서 r개를 택하는 경우의 수

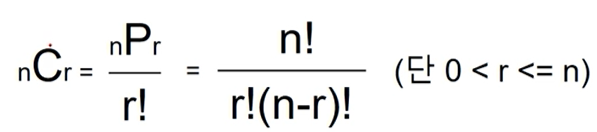
결국 순열을 구하고 r!으로 나눠주면 된다.

📌 확률

모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것.
특정사건 : 사건 (이벤트)
모든사건 - > 표본공간 (샘플)

조합을 만드는 식을 함수로 만든 뒤, 전체 경우의 수(샘플)과 사건1과 사건2를 구한다. 그러면 확률을 구할 수 있다.
probability = (event1 * event2) / sample

📖 흥미로운 점 / 새로 알게된 점

• 팩토리얼의 재귀함수 표현

  def factorialFun(n):
      if n == 1: return 1 # n이 1이라면 1을 리턴
  
      return n * factorialFun(n - 1) # n-1로 다시 함수로 들어감
  
  inputN = int(input('n 입력: '))
  print('{} 팩토리얼: {}'.format(inputN, factorialFun(inputN)))

  -> if n == 1: return if구문에서 : 다음에 개행 안해도 된다.
  -> return에 다시 실행함수를 넣을 수 있다는 아이디어

📖 이후 학습 계획

• 코딩 연습문제
  • 약수와 소수
  • 소인수와 소인수분해
  • 최대공약수
  • 최소공배수
  • 진법
  • 등차 수열
  • 등비 수열
  • 시그마
  • 계차 수열
  • 피보나치 수열