
📔 Momentum?
전통 퀀트 투자 전략에 관심이 있는 투자자라면, 모멘텀이라는 용어는 익숙히 다가올 것이다. 모멘텀은 물리학에서 사용되는 용어로, 물질의 운동량이나 가속도를 의미한다. 그렇다면, 금융학에서 모멘텀은 어떠한 의미를 담고 있는가?
달리는 말에 올라탈 준비는 되셨습니까?
위의 격언이 모멘텀을 가장 잘 설명하는 문구라고 할 수 있겠다. 즉, 금융학에서 모멘텀은 자산 가격의 상승, 또는 하락하는 추세를 의미한다. 더 나아가, 과거 수익률의 추세를 기반으로 자산의 미래 방향성을 예측하고, 투자하는 것을 모멘텀 투자라고 이야기한다.
📔 Types of momentum
모멘텀 투자 전략은 투자 방식에 따라 다양히 구분되어진다. 본 포스트에서는 간략히 3가지를 언급한 뒤, 이 중 시계열 모멘텀(Time-series momentum) 전략에 대해 자세히 다뤄보고자 한다.
모멘텀 투자 전략의 종류:
1. 시계열 모멘텀 (Time-series momentum)
위험 자산과 무위험 자산, 두 개의 자산을 기반으로 투자하는 전략. 위험 자산의 과거 수익률을 측정하고, 도출되는 결과를 통해 두 개의 자산 중 하나에 투자한다. 절대 모멘텀 투자 전략으로 언급되는 경우도 있다.
2. 횡단면 모멘텀 (Cross-sectional momentum)
다수의 위험 자산들을 기반으로 투자하는 전략. 위험 자산들의 과거 수익률을 측정하고, 도출되는 결과를 바탕으로 위험 자산간의 순위를 매긴다. 이후, 상위 % decile에 속하는 위험 자산들은 long, 하위 % decile에 속하는 위험 자산들은 short하는 Long-Short 투자 전략이다. 상대 모멘텀 투자 전략으로 언급되는 경우도 있다.
3. 듀얼 모멘텀 (Dual momentum)
시계열 모멘텀 전략과 횡단면 모멘텀 전략을 모두 활용함으로써 각자가 갖는 단점들을 보완한 투자 전략. 특히, 모든 위험 자산의 수익률이 음수인 경우에도 long하거나, 양수인 경우에도 short하는 횡단면 모멘텀 전략의 단점을 시계열 모멘텀 전략의 threshold와 무위험자산을 활용하여 보완하였다.
📔 Time-series momentum
0. 시계열 모멘텀 전략이란
과거의 추세가 오늘의 수익률을 결정한다.
앞서 언급하였듯, 시계열 모멘텀 전략은 위험자산과 무위험자산, 총 두 가지의 자산만을 활용하여 구현되는 모멘텀 전략이다.
시계열 모멘텀 전략의 매커니즘은 단순하다. 일례로, 해당 투자 전략을 운용하는 투자자 A가 있다고 하자. A는 위험자산과 무위험자산, 두 가지 자산만을 활용해 투자 전략을 운용한다. A는 현 시점으로부터 위험자산의 과거 12개월 수익률이 양수일 경우 향후 1개월간 위험자산에 투자하고, 반대의 경우 향후 1개월간 무위험자산에 투자한다. 즉, A는 위험자산의 시계열 데이터로 계산한 과거 12개월 수익률을 토대로 해당 자산이 상승 추세를 이어갈 것인지 여부를 판단하는 셈이다.
우리는 이와 같은 투자 전략을 12개월 시계열 모멘텀 전략이라고 이야기한다.
1. 하이퍼파라미터
특정 모델에서 사용자가 직접 설정하는 변수
시계열 모멘텀 전략에는 다양한 하이퍼파라미터가 존재한다.
일례로, 앞서 언급한 투자자 A의 투자 전략으로 돌아가 보자. A는 위험자산의 과거 12개월 수익률을 바탕으로 향후 1개월간 투자 판단을 내린다. 또한, 이분법적 상황에 맞춰 두 개의 자산(위험, 무위험) 중 하나에 투자하는만큼, 각 자산의 비중은 100%와 0%로 이루어진다. 이 때, 과거 12개월과 향후 1개월이라는 기간, 그리고 각 자산의 비중은 모두 A가 임의적으로 설정한 하이퍼파라미터다.
그렇다면, A는 어떠한 근거를 기반으로 위의 하이퍼파라미터를 설정했을까? 시계열 모멘텀 전략을 운용하기 전, A는 해당 전략의 효능을 확인하기 위해 1990/01/31 ~ 2021/11/31까지의 1개월 단위 시계열 데이터를 바탕으로 백테스트를 진행했다. 하이퍼파라미터에 다양한 수치들을 대입하며 벤치마크(Benchmark; BM) 대비 좋은 성과를 찾고자 노력했고, 상단의 하이퍼파라미터 조합이 가장 좋은 성과를 제공함을 확인했다.
하이퍼파라미터는 다양한 근거를 기반으로 자율적으로 설정될 수 있다. 하단의 테이블은 시계열 모멘텀 전략에 존재하는 하이퍼파라미터를 간략히 소개한다.
| 하이퍼파라미터 | 설명 | 예시 |
|---|---|---|
| 기간 | 자산 시계열 데이터의 기간 | 1990/01/31 ~ 2021/11/31 |
| 단위 | 자산 시계열 데이터의 단위 | 1개월 단위 데이터 |
| 모멘텀 측정 기간 | 추세를 파악하기 위해 계산되는 과거 수익률 기간 | 과거 12개월 |
| 비중 | 포트폴리오 내 각 자산에 투자되는 정도 | 100%, 0% |
| 리밸런싱 기간 | 자산의 비중을 재조정하는 기간 | 1개월 |
| 투자 전략 구현 방식에 따라 추가 가능 |
2. 자산의 가격
본격적으로 시계열 모멘텀 전략을 구현해보자.
가장 먼저, 위험자산과 무위험자산을 설정하자. 두 자산은 투자자의 자율적인 설정이 가능하다. 일례로, 위험자산으로 KOSPI200 지수추종 ETF인 KODEX200, 그리고 무위험자산으로 CD금리를 활용할 수 있겠다.
위험자산을 , 무위험자산을 , 그리고 기간을 ~ , 단위를 이라고 하겠다. 이를 바탕으로 시점의 위험자산 가격을 , 무위험자산 가격을 로 표기할 경우, 가격 데이터프레임은 다음과 같이 구성된다:

유의점:
는 현재 시점을 의미한다.
또한, ~ 까지의 가격 데이터프레임은 모두 과거의 가격 데이터를 칭한다.
3. 자산의 수익률
앞서 구현한 두 자산의 가격 데이터프레임을 토대로 각 자산의 기간별 수익률을 계산하겠다. 자산의 시점 가격을 , 시점 수익률을 라고 할 때, 수익률 는 다음의 산식을 통해 도출된다:
상단의 산식을 바탕으로 시점의 위험자산 수익률을 , 무위험자산 수익률을 로 표기할 경우, 수익률 데이터프레임은 다음과 같이 구성된다:
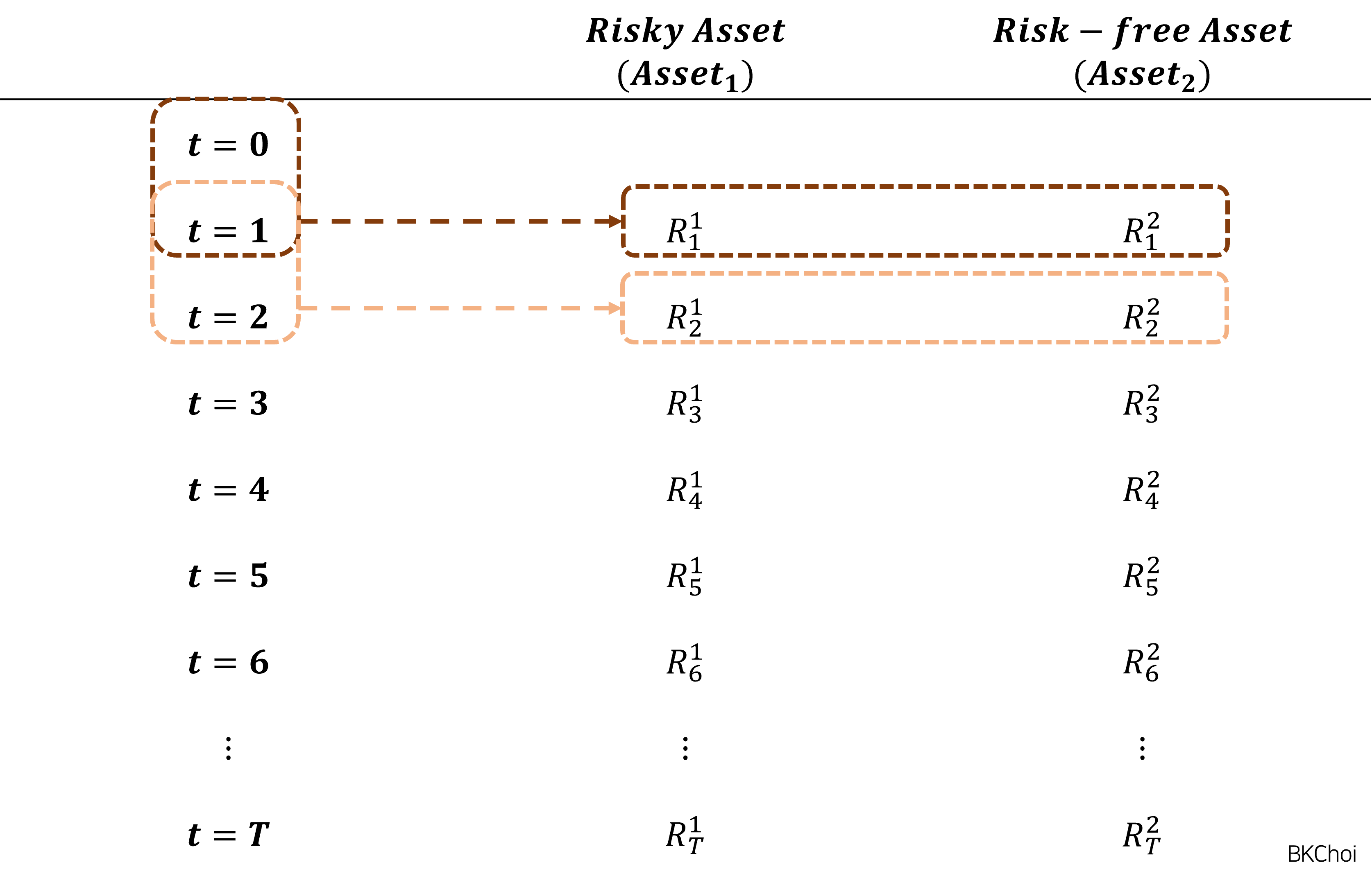
유의점:
수익률 데이터프레임은 시계열 모멘텀 전략의 백테스트를 진행할 때 사용된다.
이는 [📔 Code Expalantion]에서 자세히 다루도록 하겠다.
4. 모멘텀 측정 기간 수익률
시계열 모멘텀 전략은 과거 수익률의 추세를 기반으로 투자 판단이 이루어진다고 이야기했다. 과거 수익률의 추세는 다음과 같은 방안을 통해 확인할 수 있다:
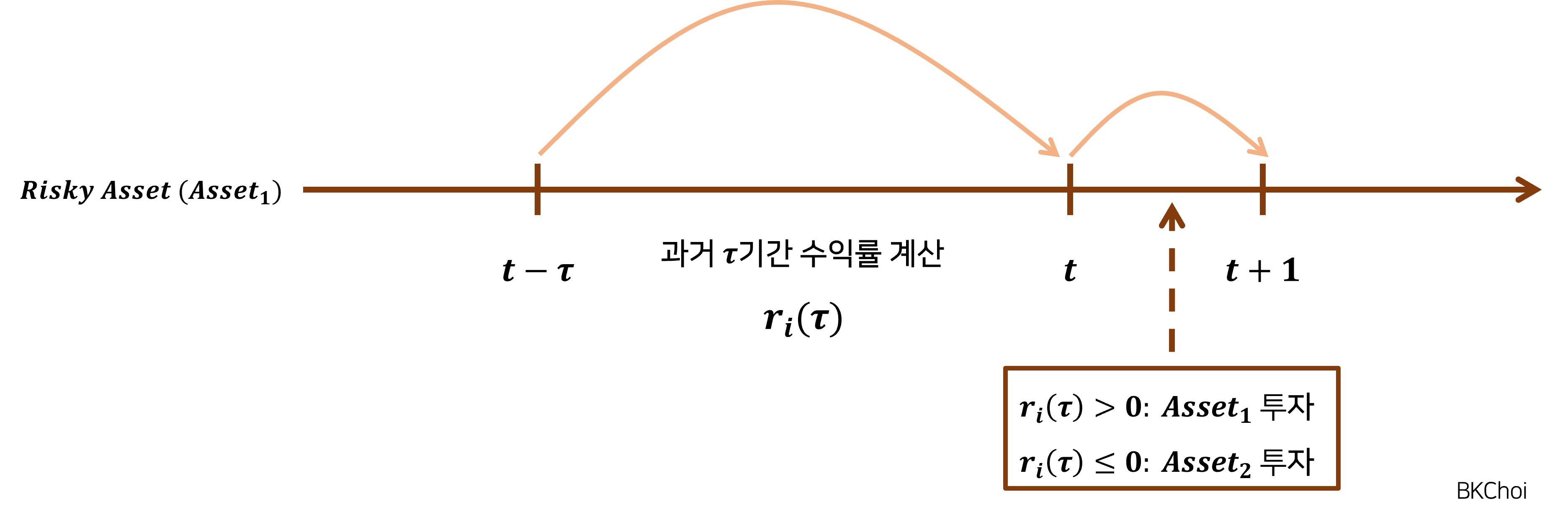
모멘텀 측정 기간을 라고 하겠다. 과거 수익률의 추세는 현 시점으로부터 자산의 과거 기간 수익률을 계산하여 확인할 수 있다. 만일 자산의 과거 기간 수익률이 양수일 경우, 자산의 가격이 상승하는 추세에 놓여있다고 이야기할 수 있다. 반대의 경우, 하락하는 추세에 놓여있다고 이야기할 수 있겠다. 앞서 언급한 투자자 A의 예시를 빌리자면, A의 기간은 12개월이었다.
수식으로 표현해보자. 위험자산의 시점 가격을 , 시점 가격을 , 기간 수익률을 라고 할 때, 수익률 는 다음의 산식을 통해 도출된다:
4-1. 중기 모멘텀 (Intermediate momentum)
앞서 과거 수익률의 추세는 시점과 시점 간의 가격을 비교하여 확인한다고 이야기했다. 바꿔 말하면, 현재 시점과 과거 시점을 비교한 셈이다. 그러나, 만일 현재가 아닌 다른 시점과 과거 시점을 비교하여 투자 판단을 내리고 싶다면?
실제로, 모멘텀과 관련한 일부 연구에 따르면, 과거 수익률의 추세에는 단기 반전 효과(short-term reversal)가 존재한다고 이야기한다. 또한, 이에 의거해 개월 시계열 모멘텀 전략 대신 개월 시계열 모멘텀 전략이 더욱 높은 성과를 제시한다고 주장한다. 이처럼, 현재가 아닌 다른 시점과 과거 시점간의 모멘텀 측정 기간을 중기 모멘텀(Intermediate momentum)이라고 이야기한다. 다음은 중기 모멘텀의 한 예시이다:
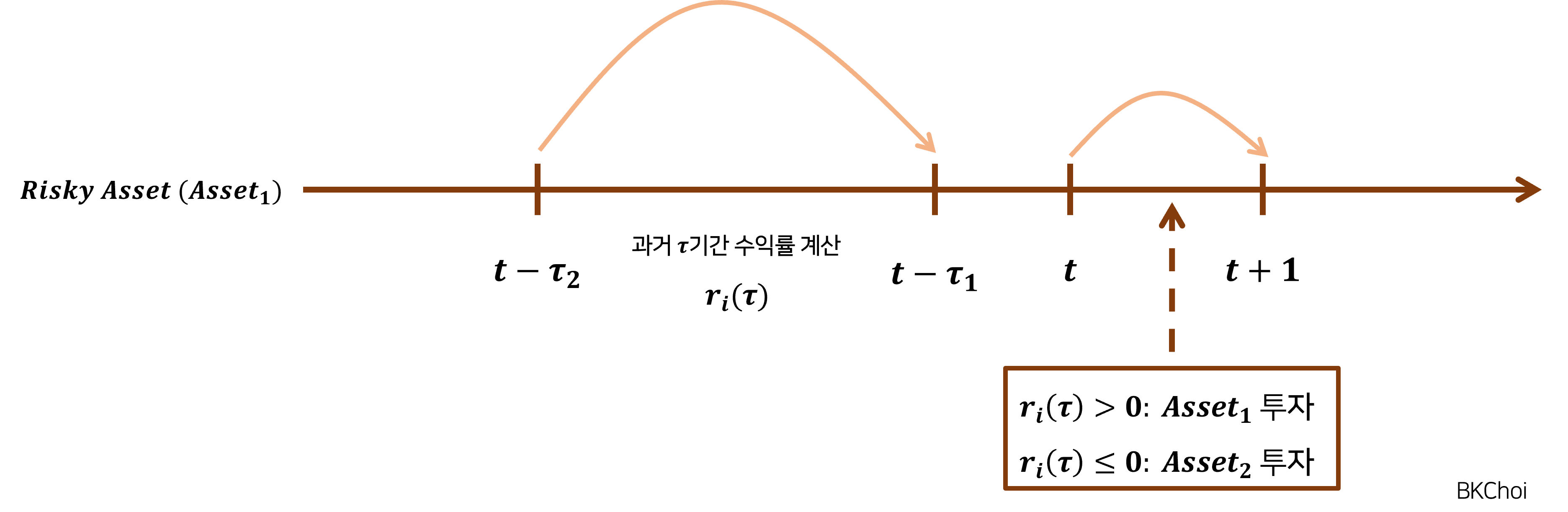
수식으로 표현해보자. 위험자산의 시점 가격을 , 시점 가격을 (, 그리고 ( ~ )기간 수익률을 라고 할 때, 수익률 는 다음의 산식을 통해 도출된다:
유의점:
[5. 투자 판단]에서 중기 모멘텀은 고려하지 않는다.
이는 [📔 Code Explanation]에서 고려될 것이다.
5. 투자 판단
앞서 계산된 를 통해 과거 수익률의 추세를 확인했다. 우리는 이를 바탕으로 위험자산의 향후 방향성을 예측할 것이며, 다음과 같이 투자를 진행할 것이다:
1. 일 경우
시점에서 시점까지 기간동안 위험자산 에 투자할 것이다.
2. 일 경우
시점에서 시점까지 기간동안 무위험자산 에 투자할 것이다.
일례로, , 그리고 리밸런싱 기간은 을 희망하는 투자자 B가 있다고 하자. 만일, ~ 까지 총 기간동안 위험자산 의 수익률이 %로 양수였다면, B는 에 ~ 까지 기간동안 투자를 진행할 것이다:
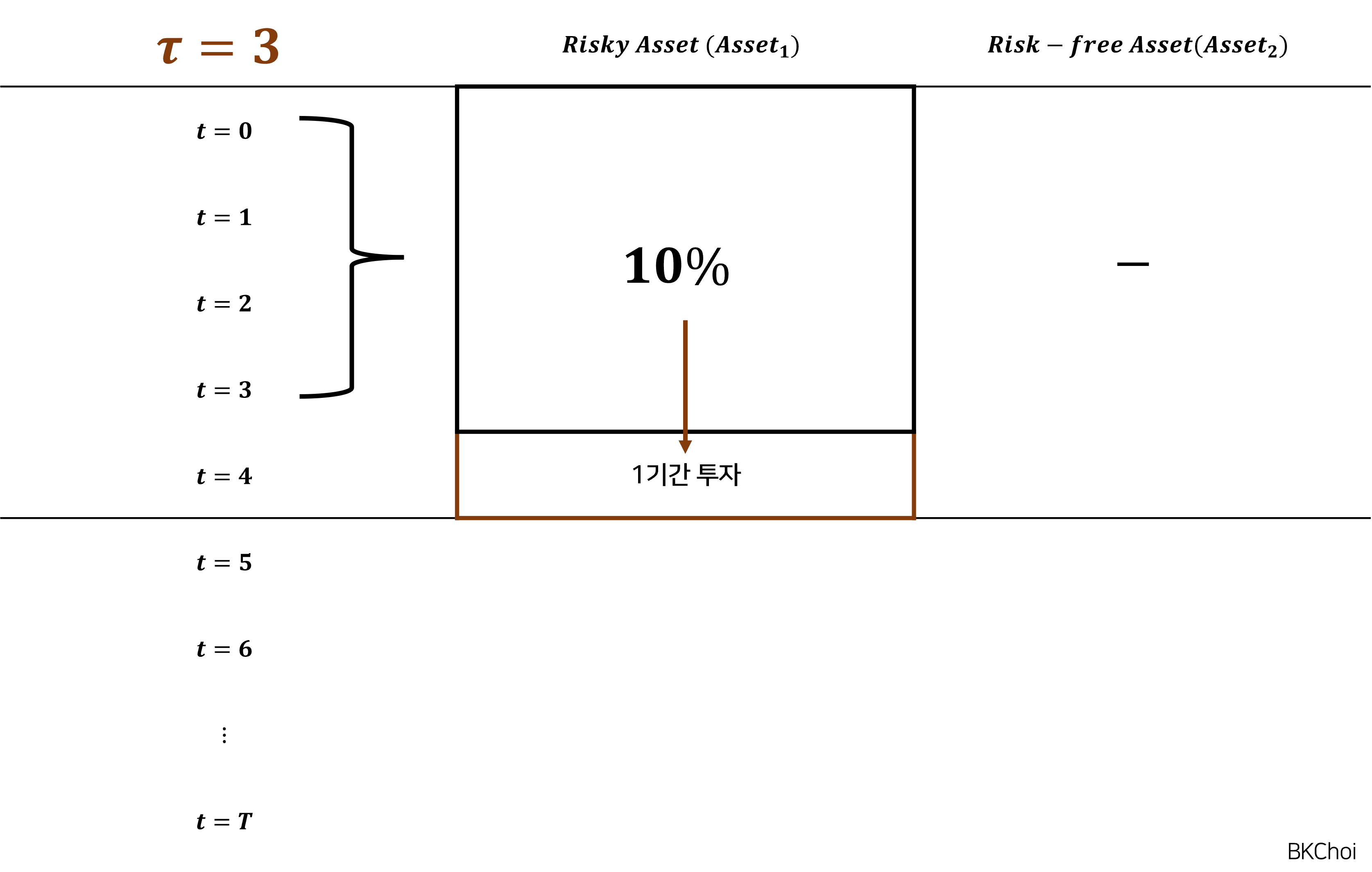
반면, 기간이 지난 뒤, ~ 까지 총 기간동안 위험자산 의 수익률이 %로 보다 작았다면, B는 무위험자산 에 ~ 까지 기간동안 투자를 진행할 것이다:
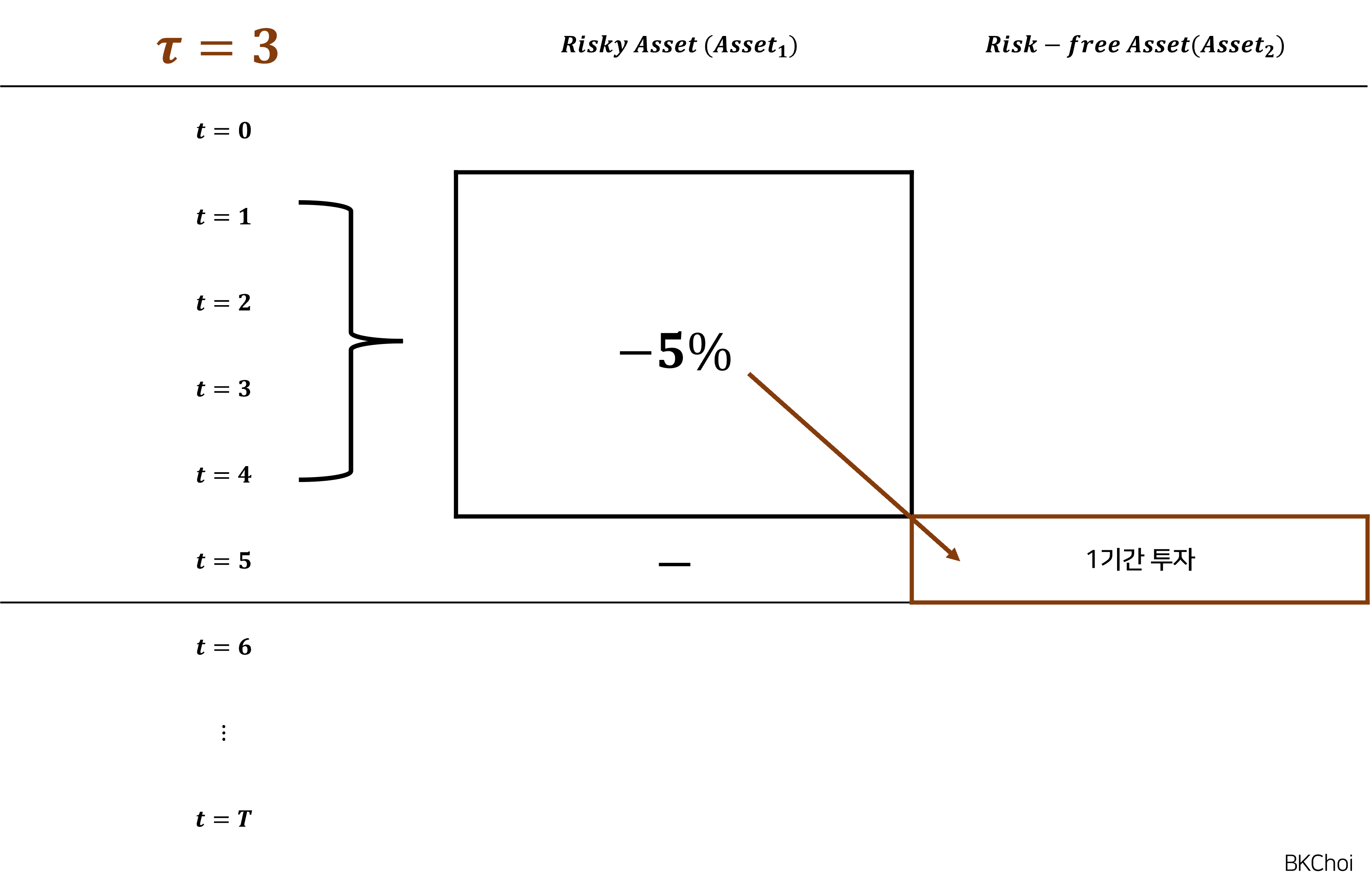
이처럼, 시계열 모멘텀 전략은 위험자산의 시계열 데이터를 기반으로 과거 수익률의 추세를 계산한 다음, 조건에 따라 위험자산 또는 무위험자산에 투자하는 전략이다.
6. 정리 및 체크
지금까지 시계열 모멘텀 전략에 대해 간략히 살펴보았다. 시계열 모멘텀 전략 코드 설명에 들어가기 앞서, 해당 전략에 대한 체크포인트를 제시하고자 한다.
시계열 모멘텀 전략 구현을 위한 체크포인트:
- 위험자산 및 무위험자산 설정
- 위험자산 및 무위험자산 가격 데이터프레임 확인 (동일 기간 / 단위)
- 위험자산 및 무위험자산 수익률 데이터프레임 구현
- 모멘텀 측정 기간() 수익률 계산
- 기간 수익률에 따른 현 시점 위험자산 및 무위험자산 투자 결정
- 백테스트 진행 및 성과 확인
📔 Code Explanation
앞서 다룬 시계열 모멘텀 전략을 Python 코드로 구현하였다.
Python 코드로 구현한 전략은 과거 수익률 추세가 양수일 경우 위험자산에 투자하고, 그렇지 않을 경우 무위험자산에 투자하는 시계열 모멘텀 전략이다.
0. Libraries
# Essential Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import gridspec
# Optional Libraries
from tqdm import tqdm1. Data
데이터 특성 및 설명
| 특성 | 설명 |
|---|---|
| 위험자산 | KOSPI200지수 |
| 무위험자산 | CD1개월 금리 |
| 단위 | 1개월 단위 데이터 |
| 기간 | 1990/01/31 ~ 2021/11/30 |
| 출처 | FnGuide & DataGuide |
| 파일 형식 | Excel(rawdata.xlsx) |
데이터 구성 예시
| Date | KOSPI200 | CD1m |
|---|---|---|
| 1990-01-31 | 97.83 | 14.00 |
| 1990-02-28 | 94.06 | 14.00 |
| 1990-03-31 | 92.10 | 14.00 |
| 2021-09-30 | 401.30 | 0.98 |
| 2021-10-31 | 388.47 | 0.94 |
| 2021-11-30 | 373.24 | 1.16 |
# Extract excel data
data_excel = pd.ExcelFile('./rawdata.xlsx')
# Convert rawdata to dataframe
data_df = data_excel.parse(sheet_name='Sheet1', index_col='Date') # Excel to dataframe
rawTime = data_df.index.copy() # Time to dataframe
rawRisky = data_df.iloc[:,0].copy() # Risky asset to dataframe
rawRf = data_df.iloc[:,1].copy() # Risk-free asset to dataframe
# Return dataframe
rawR1 = rawRisky.pct_change() * 100 # Risky asset return dataframe (%)
rawR2 = rawRf.shift(1)/12 # Risk-free asset return dataframe (Chracteristic of interest)2. Time-series momentum function
# Hyperparameters
# lag2 = past period
# lag1 = past period (lag2 is closer to present period than lag1)
# data_time = date dataframe (Ex.rawTime)
# data_Risky = risky asset dataframe (Ex.rawRisky)
# return_Risky = risky asset return dataframe (Ex.rawR1)
# return_Rf = risk-free asset return dataframe (Ex.rawR2)
# stDtaeNum = Back-test starting date (Ex.'19941228')
# stMoney = Initial amount invested (Ex.100)
# Time-series momentum(TSM) function
def TSM(lag2, lag1, data_Time, data_Risky, return_Risky, return_Rf, stDateNum, stMoney):
# Momentum observation parameters
tau = lag1 - lag2
rawMom = data_Risky.shift(lag2).pct_change(tau) * 100 # Momentum return dataframe
rawSignal = 1 * (rawMom > 0) # Signal(weight) dataframe
# If the value in momentum return dataframe(rawMom) is >0, invest to risky asset (1)
# If the value in momentum return dataframe(rawMom) is <0, invest to risk-free asset (0)
# Back-testing
stDate = pd.to_datetime(str(stDateNum), format = '%Y%m%d') # Back-test starting date
# Slice dataframes to back-test starting date
Time = data_Time[data_Time >= stDate].copy()
R1 = return_Risky[data_Time >= stDate].copy()
R2 = return_Rf[data_Time >= stDate].copy()
Signal = rawSignal.iloc[data_Time >= stDate].copy()
numData = Time.shape[0] # Length of data used in back-testing
# Weight dataframe
W1 = Signal
W2 = 1 - W1
# Portfolio return & value series
Rp = pd.Series(np.zeros(numData)) # Return series
Vp = pd.Series(np.zeros(numData)) # Value series
Vp[0] = stMoney # Initial amount invested in TSM portfolio
for i in range(1, numData):
Rp[i] = W1[i-1] * R1[i] + W2[i-1] * R2[i] # Return calculation for TSM
Vp[i] = Vp[i-1] * (1 + Rp[i]/100) # Value calculation for TSM
# Drawdown
MAXp = Vp.cummax()
DDp = (Vp / MAXp - 1) * 100
# Optional calculation for performance observation
# CAGR calculation
CAGR = round(((Vp.iloc[-1] / Vp.iloc[0]) ** (1/12) - 1) * 100,2)
if lag1 <= lag2:
CAGR = 0
# Sharpe Ratio calculation (* Risk-free asset not considered)
Sharpe = round(np.mean(Rp) / np.std(Rp) * np.sqrt(12), 2)
if lag1 <= lag2:
Sharpe = 0
# Final datas to be extracted
return Time, Rp, Vp, DDp, CAGR, Sharpe3. Benchmark function
벤치마크(Benchmark; BM)는 위험자산으로 활용한 KOSPI200지수를 사용했다.
# Hyperparameters
# data_time = date dataframe (Ex.rawTime)
# data_Risky = risky asset dataframe (Ex.rawRisky)
# stDtaeNum = Back-test starting date (Ex.'19941228')
# stMoney = Initial amount invested (Ex.100)
# Benchmark function
def BM(data_Time, data_Risky, stDate, stMoney):
# Slice dataframes to back-test starting date
BM = data_Risky[data_Time >= stDate].copy()
Rb = return_Rf[data_Time >= stDate].copy()
# Value
Vb = (BM / BM[0]) * stMoney
# Drawdown
MAXb = Vb.cummax()
DDb = (Vb / MAXb - 1) * 100
# Final datas to be extracted
return Vb, DDb4. Graphs
앞서 구현한 시계열 모멘텀 전략 코드(TSM)를 활용해 12개월, 9개월, 6개월, 3개월, 12-1개월 시계열 모멘텀 전략의 Value와 Drawdown을 도출했다.
TSM 함수 구성 예시
| 파라미터 | 설명 |
|---|---|
| lag2 | 0, 1 |
| lag1 | 12, 9, 6, 3 |
| data_Time | rawTime |
| data_Risky | rawRisky |
| return_Risky | rawR1 |
| return_Rf | rawR2 |
| stDate | '19941228' |
| stMoney | 100 |
# 12month TSM
Time, Rp, Vp, DDp, CAGR, Sharpe = TSM(0,12,rawTime,rawRisky,rawR1,rawR2,'19941228',100)
#9, 6, 3, 12-1 TSM
Vp_2, DDp_2 = TSM(0,9,rawTime,rawRisky,rawR1,rawR2,'19941228',100)[2:4]
Vp_3, DDp_3 = TSM(0,6,rawTime,rawRisky,rawR1,rawR2,'19941228',100)[2:4]
Vp_4, DDp_4 = TSM(0,3,rawTime,rawRisky,rawR1,rawR2,'19941228',100)[2:4]
Vp_5, DDp_5 = TSM(1,12,rawTime,rawRisky,rawR1,rawR2,'19941228',100)[2:4]
# Graph
fig = plt.figure(figsize=(10, 7))
gs = gridspec.GridSpec(nrows=2,
ncols=1,
height_ratios=[8, 3],
width_ratios=[5])
ax0 = plt.subplot(gs[0])
ax0.plot(Time, Vp, label='Mom_12')
ax0.plot(Time, Vp_2, label='Mom_9')
ax0.plot(Time, Vp_3, label='Mom_6')
ax0.plot(Time, Vp_4, label='Mom_3')
ax0.plot(Time, Vp_5, label='Mom_12-1')
ax0.plot(Time, Vb, label='K200')
ax0.set_title('<Value>')
ax0.grid(True)
ax0.legend()
ax1 = plt.subplot(gs[1])
ax1.plot(Time, DDp, label='Mom_12')
ax1.plot(Time, DDp_2, label='Mom_9')
ax1.plot(Time, DDp_3, label='Mom_6')
ax1.plot(Time, DDp_4, label='Mom_3')
ax1.plot(Time, DDp_5, label='Mom_12-1')
ax1.plot(Time, DDb, label='K200')
ax1.set_title('<Draw-down>')
ax1.grid(True)
plt.show()Graph는 다음과 같이 도출된다:
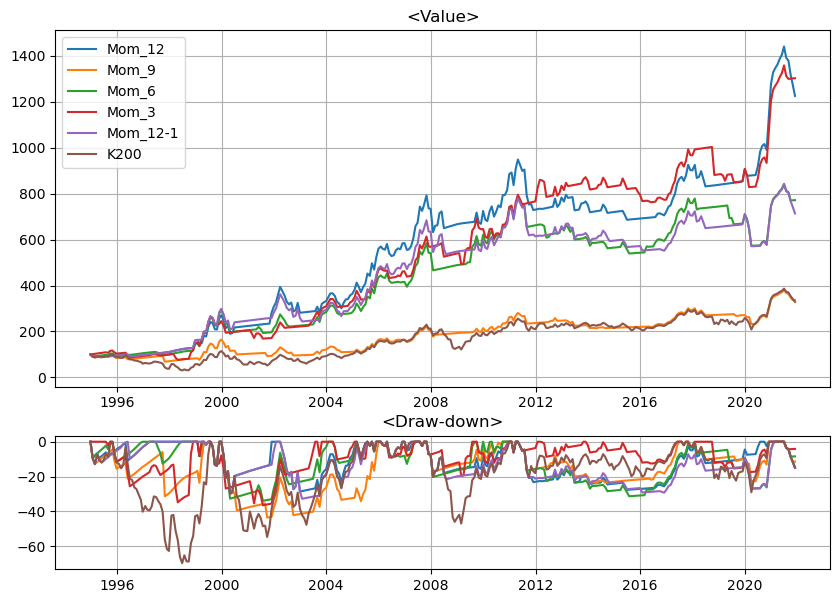
📔 마치며
이상으로 시계열 모멘텀 전략 포스트를 마치겠다.
향후 포스트에서는 CAGR과 Sharpe Ratio, 그리고 Pandas의 pivot table을 활용해 최적의 시계열 모멘텀 전략 도출, rolling return을 활용한 투자 전략 성과의 시각화, 시계열 모멘텀 전략의 성과 분석, 그리고 평균 시계열 모멘텀(Average time-series momentum) 전략에 대해 다뤄보겠다.
출처:
Thumbnail Arrow:
본 포스트는 숭실대학교 금융학부 데이터 기반 투자전략 수업자료를 활용하여 제작되었습니다.
학부생으로서 직접 배운 것을 바탕으로 작성된 포스트로, 오류가 존재할 수 있습니다.


좋은 글 감사합니다, 논리 따라가면서 구현해보니까 배우는게 많네요^^
한가지 궁금한 점이 있는데 무위험 자산(여기서는 cd금리)의 수익률을 구하실 때 12로 나눠주셨는데 그 이유가 있을까요??