0. Intro

딥러닝을 공부하다 보면 수학을 정말 빼놓을 수 없다.
최적화 문제 해결 부터가 일단 테일러 급수(Taylor Series)를 사용하는 Gradient Descent 방식을 사용하기도 하고,

일단 Vision AI의 기본 input data 자체가 행렬, Matrix이다.

그리고 Computer Graphics 의 Transform, Rotation, Scaling 이런 것들을 보면 전부 수학식, 특히 Matrix를 사용한다.

그래서 내 예상으로는, 머신러닝 & 딥러닝 하시는 분들은 아마 통계학이나 선형대수학 쪽을 많이 공부하셨을 것이라고 생각한다.

수학 시리즈에서는, 내가 개인적으로 공부한 수학 관련 글들을 아카이빙 하는 겸으로 해서 포스팅을 할 생각이다.

첫 포스팅은 정말 재밌는 삼각함수의 기초에 관련된 포스팅이다.

시작하기 전에, 수학 시리즈에 대한 나의 생각들이다.

1. 수학 시리즈의 포스팅은, 내가 메모한 노트 이미지를 업로드하고 간단한 코멘트를 덧붙이거나,
   해당 부분에 대한 느낀점을 작성하는 것으로 할 것이다.
2. 규격 같은건...없다... 단지 내가 공부했다는 것을 공유하고 싶을 뿐이다.
3. 그러므로, Rough 하게 작성하고 싶다!
4. 개인적으로 선형대수학을 굉장히 좋아한다. (세상은 선형대수학이 구원하지 않을까?)
5. 컴퓨터 그래픽스를 좋아하는 이유는, (개인적 의견으로는)수학적으로 가장 직접적이고 완벽하게 접근 가능한 부분이라고 생각해서이다.
   Computer vision 역시 수학적인 접근이 가능하지만, 공학적인 요소가 강하지만 Computer Graphics는 순수 수학적인 요소가 꽤 강하다고 생각한다.
6. 틀릴 확률이 매우 높다. 강의 같은 걸 듣고 배우는게 아니라, 그냥 혼자 독학하는 것이다...🥲
7. 외부의 정보들을 전혀 삽입하지 않을 예정이다. 그림이 필요하면 내가 그릴 것이다.
8. 현재는 선형대수학을 목표로 하고 있으며, 주된 내용은 벡터와 행렬, 차원 변환, 삼각함수, 푸리에, 테일러 등을 다루고 싶다.
9. 만약 선형대수학을 한번 쭉 본 이후 목표
   • Computer Graphics 에서의 수학
   • 미적분학
   • 선형대수학의 공학적 부분
     (공학도로써 공학과 연관지어야 하는 것은 맞지만, 그러자니 수학과 너무 멀어지는 것에 대해 싫증이 생겼다. np.linalg.norm 같은 걸 쓰면 모든 것이 해결되니...)
   • 공업수학
10. ... 제발 끝까지 보고싶다. 반복적으로 죽을 때까지 수학을 달고 살아야 하지 않을까.

1. 사인, 코사인, 탄젠트

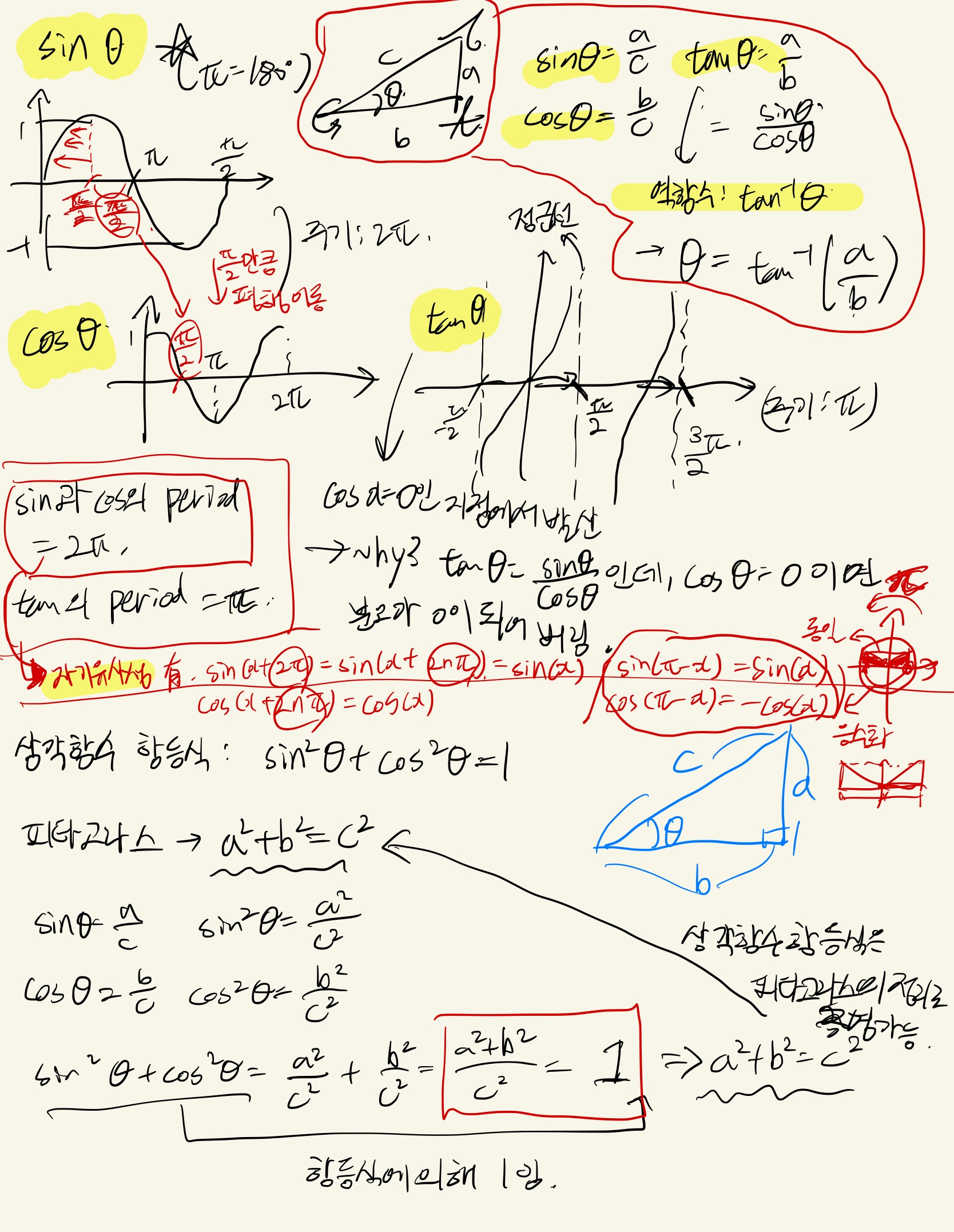
sin, cos, tan는 고등학생때 배웠었나? 그랬던 것 같다.

모든 것의 시작은 피타고라스의 정리

$a^2 + b^2 = c^2$

에서 시작한다고 생각한다. 이 수식에서 가장 중요한 삼각함수 항등식 이 나온다.

$tan(\theta)$ 는 $\frac{sin(\theta)}{cos(\theta)}$ 로 나타낼 수 있는데,
$tan(\theta)$ 그래프를 보면 $\frac{\pi}{2}$, $\frac{3\pi}{2}$ 에서 값이 발산하게 되는데,

저 $\frac{\pi}{2}$, $\frac{3\pi}{2}$ 부분이 $cos(\theta)$ 에서 0이 되는 부분이다.

$cos(\theta) = 0$ 이라면, $tan(\theta)$ 의 분모가 0이 되어버린다.

(참고로, $sin(\theta)$ 과 $cos(\theta)$ 의 주기는 $2\pi$, $tan(\theta)$ 의 주기는 $\pi$ 이다.)

---

2. 원(Circle)의 관점에서 본 삼각함수

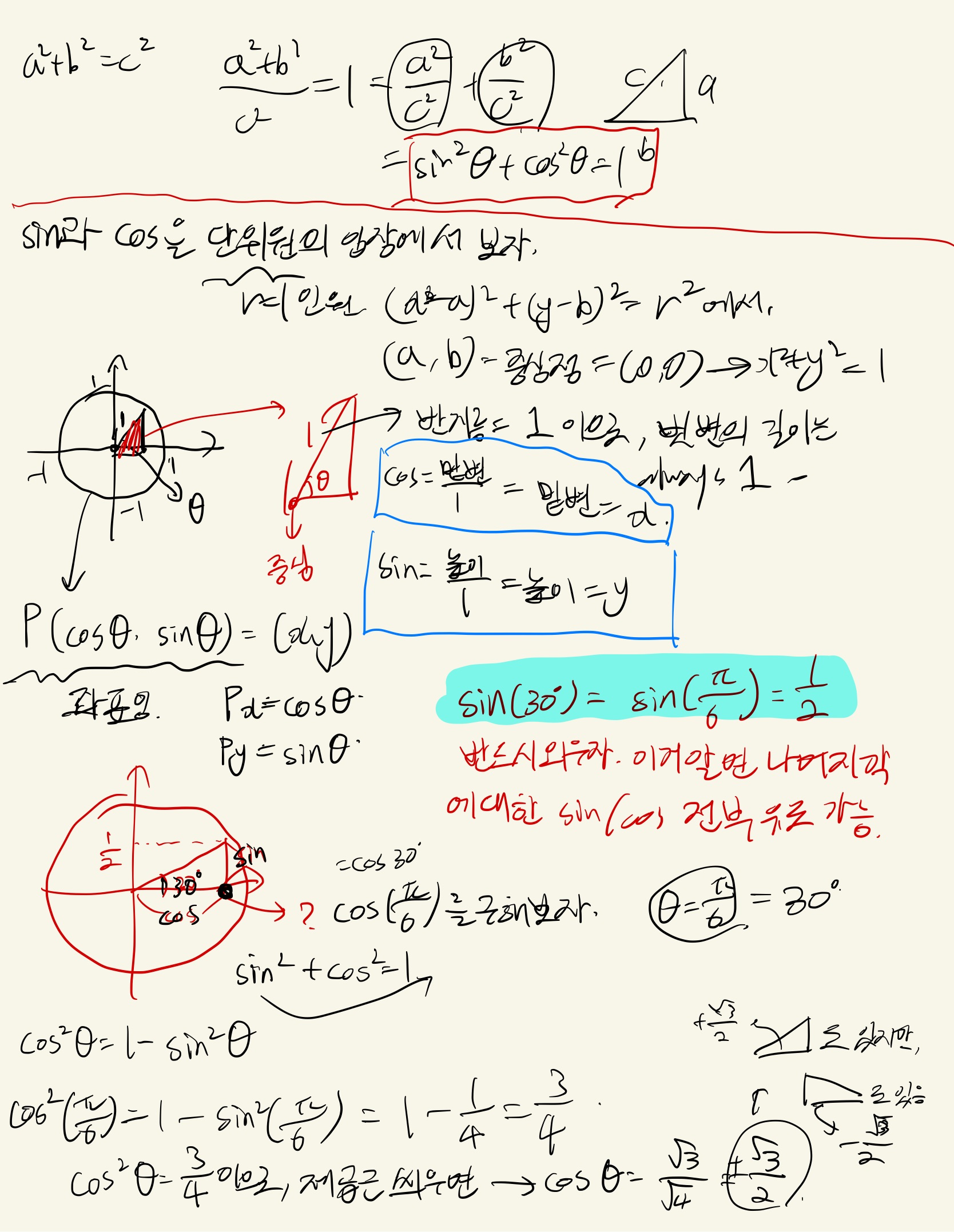
단위원 : $r=1$ , 반지름이 1인 원.

최대 값 = 최소값 = 1
여기서 왜 $x$ 좌표가 $cos(\theta)$ 이고, $y$ 좌표가 $sin(\theta)$ 인지 적어두었다.

그리고 가장 중요한

$sin(\frac{\pi}{6}) = sin(30\,^{\circ}) = \frac{1}{2}$

도 반드시 기억해야 한다. (참고 : $\pi = 180\,^{\circ}$)

위의 $sin(\frac{\pi}{6}) = \frac{1}{2}$ 을 사용하면 여러 각도에 대한 $sin$, $cos$ 값들을 구할 수 있다.

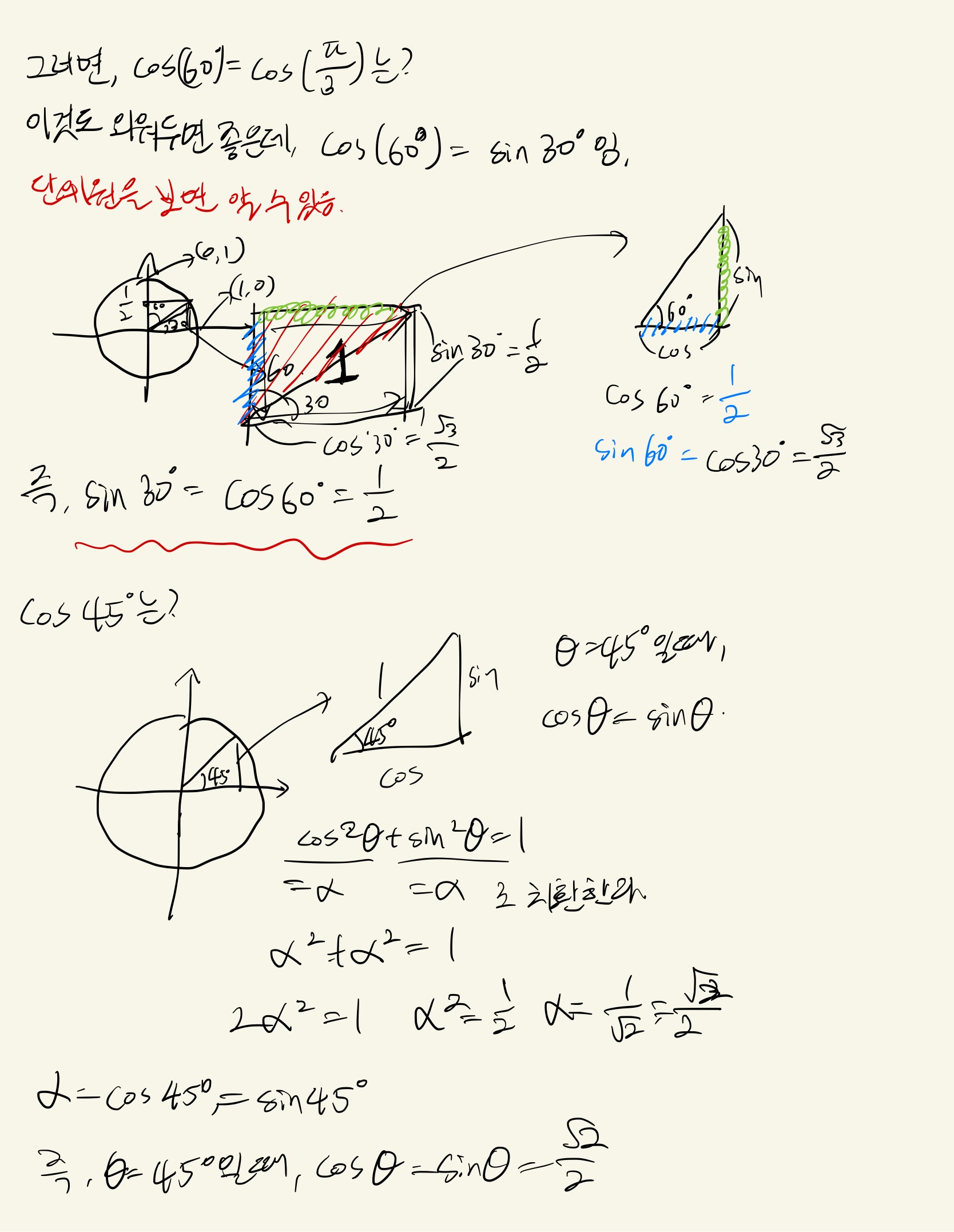
이런식으로, $cos(60\,^{\circ})$ 또는 $cos(45\,^{\circ})$ 를 위의 $sin(30\,^{\circ})$를 사용해서 구할 수 있다.

---

3. 삼각함수의 여러 공식

꼭 외워야 하는 삼각함수 항등식 뿐만 아니라, 2개를 기본적으로 먼저 보았다.

• 사인 합차 공식 : 사코 + 코사
• 코사인 합차 공식 : 코코 - 사사

그 아래는 합차 공식의 파생(?)인 배각 공식이 나온다.
배각 공식은, 내가 해보니까 굳이 외울 필요는 없다. 사인 합차 공식과 코사인 합차 공식만 알면 간단하게 유도가 가능하다.

위의 작은 수식은 배각 공식을 사용해서 $cos(30\,^{\circ})$ 과 $sin(60\,^{\circ})$ 이 서로 같은 값이라는 것을 보였다.

그리고, 반각 공식 과 사인 법칙, 코사인 제 1법칙, 코사인 제 2법칙 도 기록하였다.

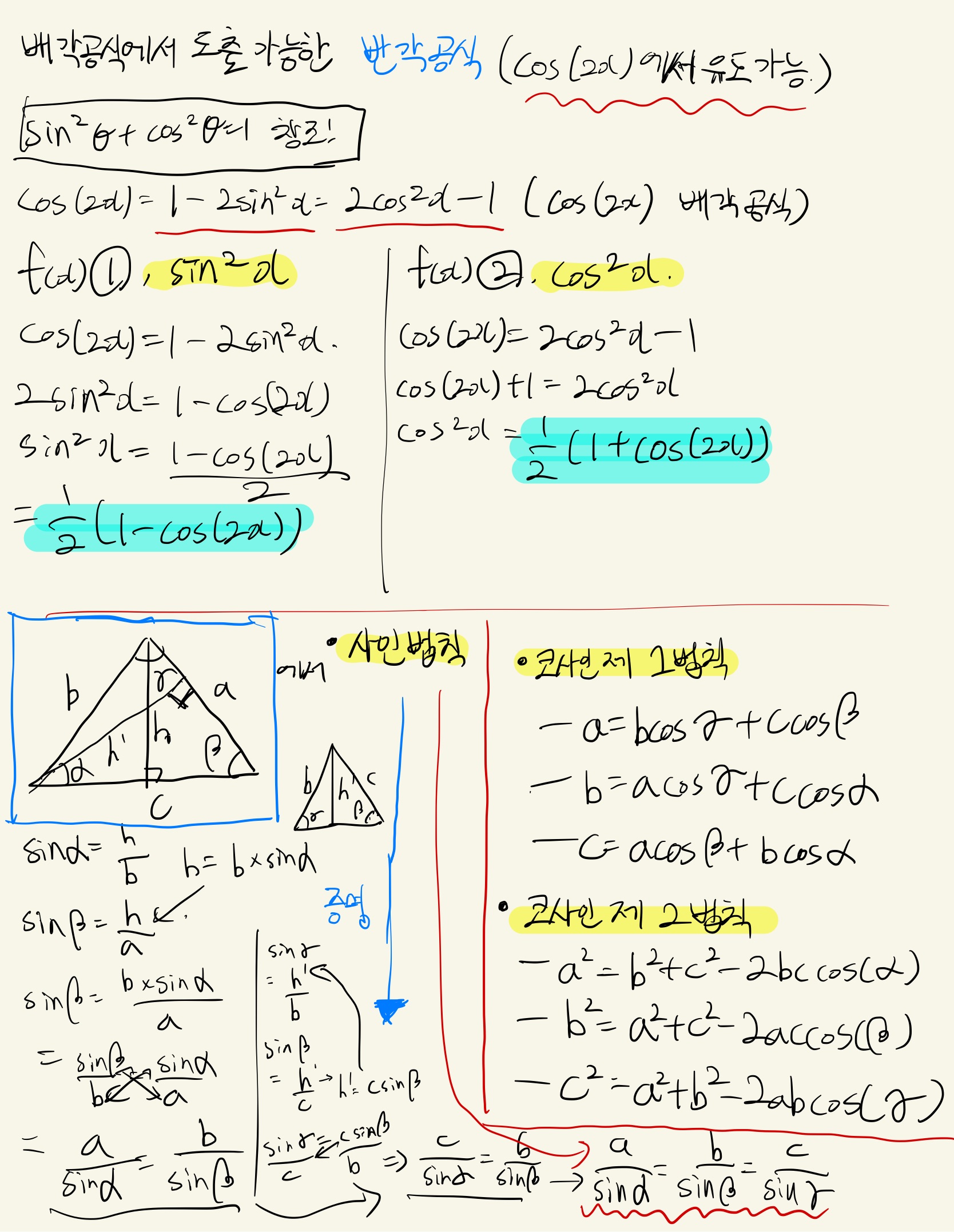
1. 사인 법칙 : 증명 기록해 뒀음.
2. 코사인 제 1법칙 : 한 변에 대한 길이인데, 구하고자 하는 변에서 수직으로 뻗는 직선을 사용하여 거기에서 나오는 $cos$ 값의 합이다. 맨 위에서 $a = b cos(\gamma) + c cos(\beta)$ 의 경우가 맨 왼쪽 그림에서 쉽게 파악할 수 있는 경우이고, 그 아래 2개의 경우($b, c$ 의 경우) 역시 파악하기 쉬울 것이다.
3. 코사인 제 2법칙 : 아래 그림 참조

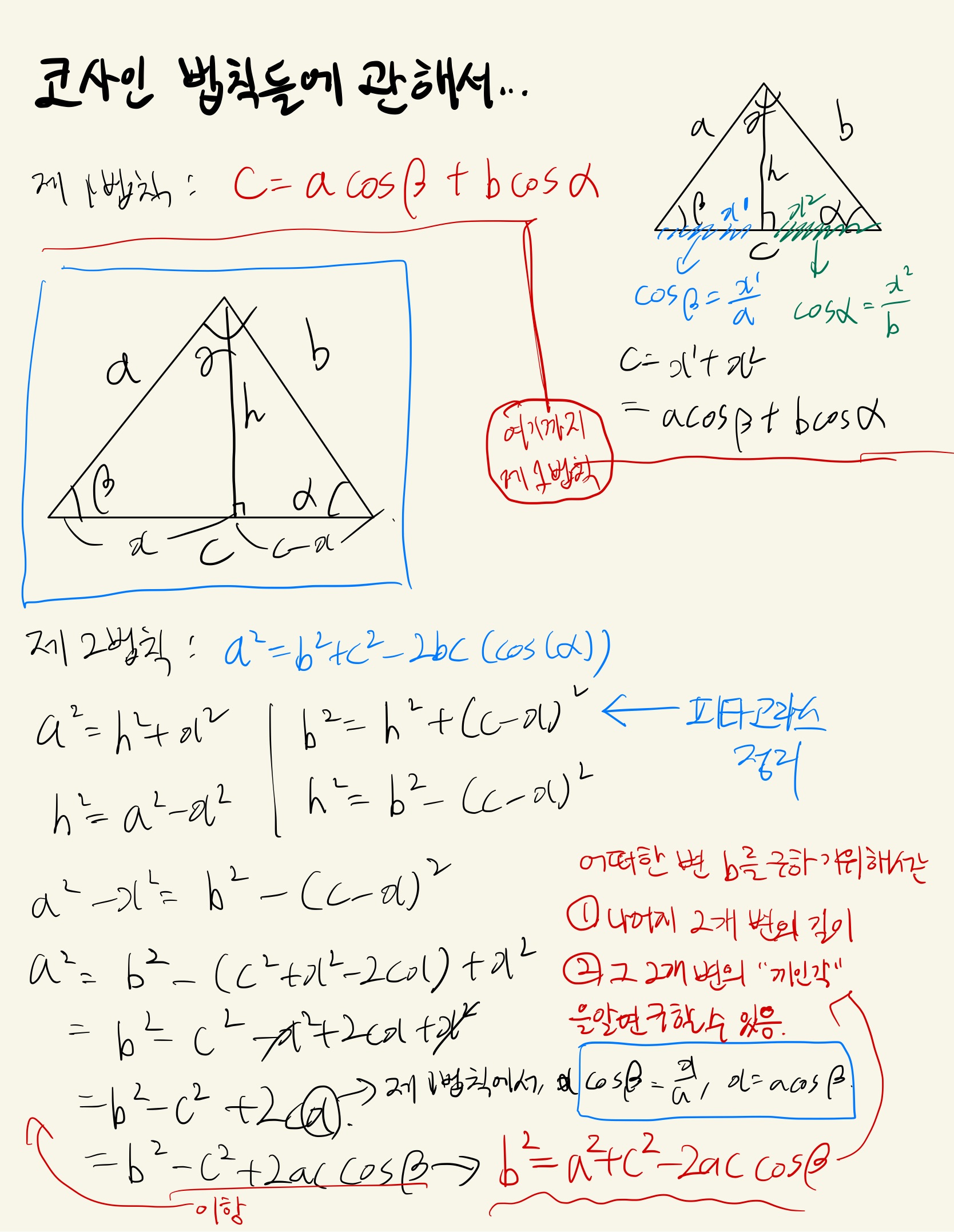
💡 코사인 제 2법칙이 의미하는 바는,

"어떠한 변 $b$의 길이를 구하기 위해서는

• 나머지 2개 변의 길이와
• 그 2개 변의 끼인각

을 알면 구할 수 있음을 의미한다.

---

알아본 것들

1. $sin, cos, tan$ 의 기본 성질(주기, 발산 위치 등)
2. 피타고라스의 정리를 이용한 공식들
   • 삼각함수 항등식
   • 사인 합차 공식
   • 코사인 합차 공식
   • 배각 공식, 반각 공식
3. 단위원과 비단위원 관점에서 본 $sin, cos$ 특정 각도에서의 값들 및 유도
4. 사인 공식 유도
5. 코사인 제 1법칙, 코사인 제 2법칙에 대한 유도, 시사점