비트연산 정복하기 -Bit Operation

앙금빵·2021년 5월 19일

자료구조와 알고리즘

목록 보기

3/5

개요

출처: Youtube: 엔지니어대한민국

하드디스크 표면

자성체로 뒤덮여 있어 바늘 끝에 코일로 자성체들의 N극과 S극의 방향을 읽을 수도 있고 그 방향을 바꾸는 방식으로 정보를 기억함 (자기장 극성 변화시 '1' 변화 없을시 '0')

CD

CD나 DVD는 매끄러운 표면에 레이저를 쏘아 정보를 저장하고 나중에 빛을 쏳아 굴곡을 읽어낸다.
굴곡의 길이가 짧으면 0 길면 1로 인식된다.
정수를 컴퓨터에 저장을 할 때 비트로 저장이 된다.
자바에서는 integer가 4 byte =32 bits (1 byte = 8 bits) 공간에 저장된다.
공간당 0과 1 로 저장이 되고 공간이 32개가 있으면 2^32 개의 저장할 수 있는 개수가 정해진다.
그러나 숫자는 0부터 시작하기때문에 표현가능한 양수는 2^32 -1 개가 된다!
정수는 양수와 음수로 나누어지기에 맨 앞의 한 칸은 +- 를 나타내는 표시로 쓴다.
0일때는 음수, 1일때는 양수를 나타낸다.
숫자는 0부터 시작하기때문에 표현가능한 양수 범위는 2^32 -1 개가 된다

출처: Youtube: 엔지니어대한민국

음수 경우 -1,...-2.. 절댓값이 커질수록 값은 감소하는 형태를 지님

고로 31개의 비트자리가 모두 1로 차지된 수가 -1을 나타낸다.

표현 가능한 수

-21억 ~ 21억

출처: Youtube: 엔지니어대한민국

이 이상의 값의 데이터 값을 이용해야 할때 다른 자료형 함수를 이용해야한다. 안그러면 오류 발생

Shift 연산

① 쌓인 비트를 무시하고 무조건 Shift

② 쌓인 비트를 염두해서 Shift 하는 방법

■ Logical Right Shift 연산: 부호를 나타내는 숫자까지 Shift, (>>>)

출처: Youtube: 엔지니어대한민국

■ Arithmetric Right Shift 연산: 부호 비트 고려하여 Shift 한다. (>>)
(수학적인 관계를 염두에 두고한다는 의미)

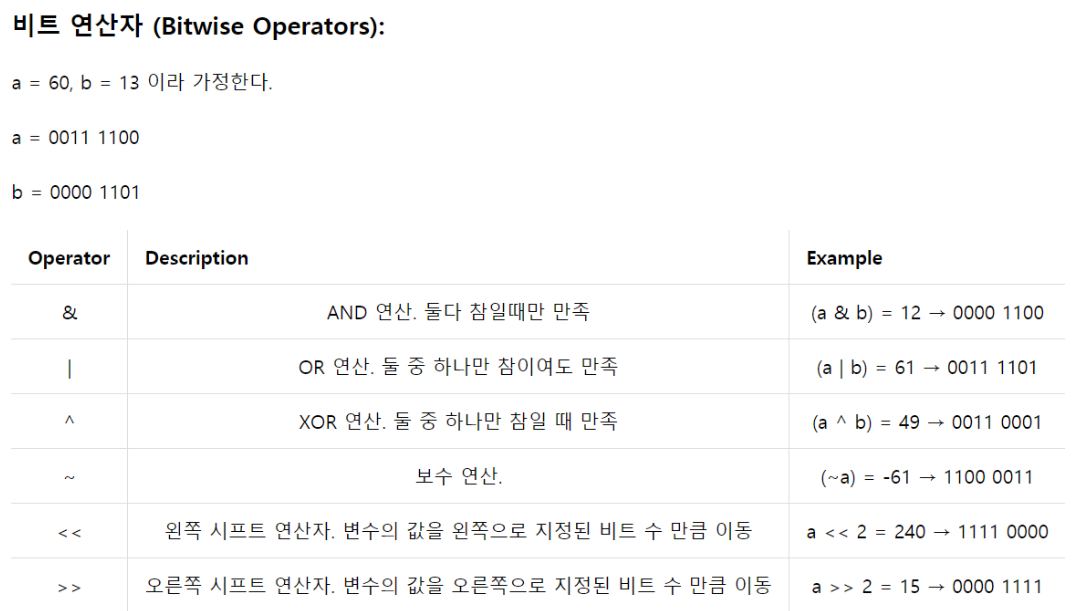
출처: Youtube: 엔지니어대한민국

비트연산자 (Python)

출처: Youtube: 엔지니어대한민국

비트 켜기 (1<<n)

n이 양수일 때, '1<<n'은 'n번째 비트를 켠다' 라는 의미를 가지고 있다.

순수한 정수 1은 비트의 세계에서는 '0번째 비트가 켜져 있다'는 동일하다.
'(1<<n)'은 0번째 켜져 있는 비트를 n만큼 왼쪽에 옮긴다는 의미이다.
즉, 결과적으로 'n'번째 비트를 켠다는 의미와 동일해진다.

def nth_bit_on(n):
	return(1<<n)

print(bin(nth_bit_on(1)))
print(bin(nth_bit_on(2)))
print(bin(nth_bit_on(3)))
print(bin(nth_bit_on(4)))

"""
0b10
0b100
0b1000
0b10000

파이썬은 0번째 부터 시작한다는 것을 주의하자
"""

n번째 비트 on/off 확인

def get_nth_bit(n,nth):
	reurn 1 if n&(1 << nth) else 0

print('10진수 100을 2진수로 변환한 값:', bin(7))
print(get_nth_bit(7,2))
"""
0b100   << 1을 2칸 이동
0b111   << 7 이진수 표현

'&' 연산이 더해지면

0b100

0이 아닌 값이 존재하므로 1 반환
"""

"""
1줄짜리 풀이
def get_nth_bit(n, nth):
    return bool(n & (1 << nth))
"""

(1<<n) -1 : n개의 비트 모두 켜기

print(bin((1 << 1) - 1))
print(bin((1 << 2) - 1))
print(bin((1 << 3) - 1))
print(bin((1 << 4) - 1))
print(bin((1 << 8) - 1))

"""
0b1
0b11
0b111
0b1111
0b11111111
"""

유용한 트릭

정수의 2의 지수승 여부 확인하기

def is_exp_binary(n):
	return n & (n-1) == 0

"""
2의 지수승이라면 10000..0000 의 형태 아니라면 어느 자리에 1이 있음
2진수 경우 정수 (n-1) 을 이진법으로 나타내면 1111...1111 형태

이 둘의 '&' 연산을 진행할 경우 0 이 나와야 한다.
"""
print(1, is_exp_binary(2 ** 0))
print(2, is_exp_binary(2 ** 1))
print(4, is_exp_binary(2 ** 2))
print(1024, is_exp_binary(2 ** 10))

print(3, is_exp_binary(3))
print(15, is_exp_binary(15))
print(101, is_exp_binary(101))
print(1000, is_exp_binary(1000))

1 True
2 True
4 True
1024 True

3 False
15 False
101 False
1000 False

Q. 2진수에서 1 비트의 개수 구하기

Method 1. 2로 나누어 가면서 나머지가 1인 것들 더하기

def count_bit(n):
	return n%2 + count_bit(n//2) if n >=2 else n

"""
재귀함수 형태

n%2 :  2로 나눈 나머지
n//2 : 2로 나눈 몫
"""

Method 2. 2로 나누는 것을 비트연산을 통해 더 빠르게 개선

def bit_count(n):
    k = 0
    count = 0

    while n >= (1 << k): # 1 0...0 (0은 k개) 가 될 때 까지
        if n & (1 << k) != 0: # k번째 자리에 1이 있다면
        	count += 1 # count +1
        k += 1

    return count

Method 3. N과 N-1 을 '&' 연산 이용

맨 오른쪽 비트가 사라지는 특성을 이용하자

def bit_count(n):
    k=0
    count=0
    while n >= (1<<k):
        print(f'전 n 2진수 {bin(n)}, 10진수 {n}')
	n=n&(n-1)
	print(f'후 n 2진수 {bin(n)},10진수 {n}')
        count +=1
        k +=1
    
    return count

"""
전 n값 0b111
후 n값 0b110
전 n값 0b110
후 n값 0b100
전 n값 0b100
후 n값 0b0

return 값 3
"""