Hash Table 파헤치기

앙금빵·2021년 5월 23일

알고리즘

자료구조와 알고리즘

목록 보기

4/5

1. Hash Table 이란?

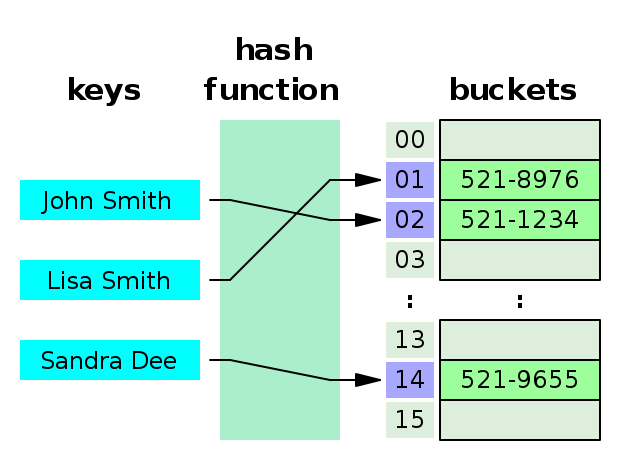
Key-Value 형태로 데이터를 저장하는 자료구조
내부적으로 배열을 이용하여 데이터를 저장 (그림 참조)
각각의 Key 값에 해시함수를 적용하여 배열의 고유한 Index를 생성한다.
생성된 Index를 활용하여 값을 저장하거나 검색한다.

2. 용어 정리 (Hash, Hash Function)

해시(Hash)

임의의 크기를 가진 데이터(Key)를 고정된 크기의 데이터(Value)로 변화시켜 '저장' 하는 것
Key에 대한 Hash 값을 구하는 과정을 'Hashing' 이라고 한다.
기본 연산으로 탐색(Search), 삽입(Insert), 삭제(Delete)가 있다. (시간복잡도: $O(1)$ )

해시 함수(Hash Function)

Key에 대한 Hash 값을 만드는 함수이다.
서로 다른 Key가 같은 Hash가 되는 경우를 해시 충돌(Hash Collision) 이라 한다.
Hash 충돌이 일어나지 않을 수록 '좋은 함수'이다. (i.e Hash 값을 고르게 만들어 내는 함수가 좋다.)

3. 해시 충돌 (Hash Collision)

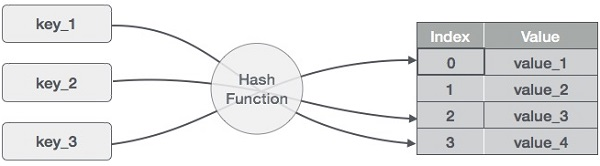
`출처: https://www.tutorialspoint.com/data_structures_algorithms/hash_data_structure.htm

해시함수를 사용하여 특정 해시 값을 알아내고 그 해시값을 Index로 변환하여 Key-Value 형태로 데이터를 저장하는 자료구조이다.
Hash Table에 있어 문제가 되는 것은 충돌(Collision)이다.

적재율(Load Factor)

적재율이란 해시 테이블의 크기 대비 키의 개수를 말한다.
키의 개수를 $K$ , 해시 테이블의 크기를 $N$ 이라 둘 때, 적재율은 $K/N$ 이다.
Direct Address Table 경우 Key값을 Index로 사용하는 구조이기 때문에 적재율이 1 이하이다.
즉, 적재율이 1이 초과되면 반드시 충돌된다.

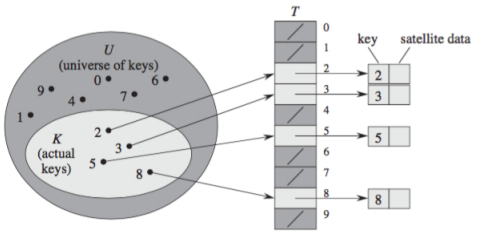
▶ 최대 키 값에 대하여 알고 있어야 한다.

▶ 키 값들이 골고루 분포 되어 있지 않다면 메모리 낭비가 심하다.

3-1. 해시 충돌해결 1안. 구조 개선

3-1-1. 분리 연결법(Seperate Chaining)

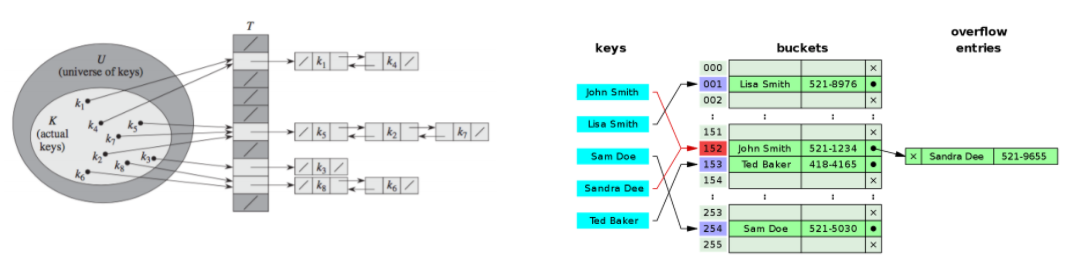
자료 저장시 충돌이 일어나면 해당 값을 기존 값과 연결시키는 기법
우측 그림에서 Sandra를 저장할 때 충돌이 발생하였고 기존 Index John 과 Chaining 했다.
즉, Index 값 충돌 시 다음에 저장된 자료를 기존 자료 다음에 위치시키는 것이다.
적재율(Load factor) $α$ = $n/m$ 이라 두면 시간복잡도는 $O(α+1)$ 이다.

# Performance of Chaining
"""
m = Number of slots in hash table
n = Number of keys to be inserted in hash table
 
 Load factor α = n/m 
  
 Expected time to search = O(1 + α)
 
 Expected time to delete = O(1 + α)

 Time to insert = O(1)

 Time complexity of search insert and delete is O(1) if  α is O(1)
"""

장점

(1) 한정된 저장소(Bucket)을 효율적으로 사용할 수 있다.

(2) 해시 함수(Hash Function)을 선택하는 중요성이 상대적으로 적다.

(3) 상대적으로 적은 메모리를 사용한다. 미리 공간을 잡아 놓을 필요가 없다.

단점

(1) 한 Hash에 자료들이 계속 연결된다면(쏠림 현상) 검색 효율을 낮출 수 있다.

(2) 외부 저장 공간을 사용하며 작업이 추가로 진행되어야 한다.

3-1-2. 개방 주소법(Open Addressing)

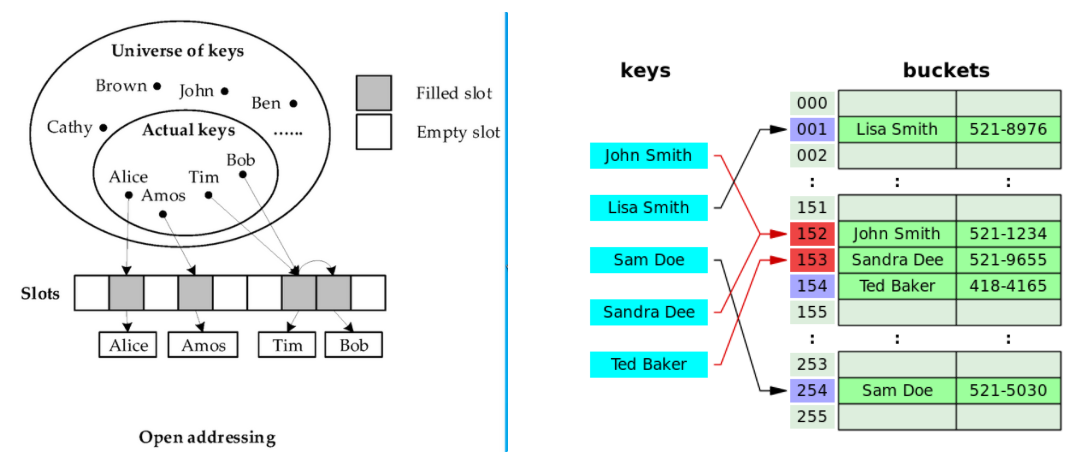
동일한 Index에 이미 다른 데이터가 존재하는 경우 다른 주소로 이용할 수 있게 하는 기법이다.
충돌 시 비어있는 주소로 저장하며 탐색, 삽입, 삭제의 과정이 이루어 진다.
(1) 삽입: 계산한 해시 값에 대한 인덱스가 이미 차있는 경우 다음 인덱스로 이동하면서 비어있는 곳에 저장한다. 이렇게 비어있는 자리를 탐색하는 것을 탐사(Probing)라고 한다.
(2) 탐색: 계산한 해시 값에 대한 인덱스부터 검사하며 탐사를 해나가는데 이 때 “삭제” 표시가 있는 부분은 지나간다.
(3) 삭제: 탐색을 통해 해당 값을 찾고 삭제한 뒤 “삭제” 표시를 한다.
Hash를 찾는 규칙에 따라 선형탐색, 제곱탐색, 이중 해시로 구분된다.
(1) 선형탐색(Linear Probing): Index n개(+n)를 건너뛰어 비어있는 해시에 데이터를 저장한다.
(2) 제곱탐색(Quadratic Probing): 충돌이 일어난 해시의 제곱을 한 Hash에 데이터를 저장한다.
(3) 이중해시(Double Hashing): 해시된 값을 한번 더 해싱하여 해시의 규칙성을 없애버리는 방식

적재율(Load factor) $α$ = $n/m$ 이라 두면 이라 두면 시간복잡도는 $O(1/α+1)$ 이다.

# Performance of Open Addressing
"""
m = Number of slots in the hash table
n = Number of keys to be inserted in the hash table
 
Load factor α = n/m  ( < 1 )
Expected time to search/insert/delete < 1/(1 - α)
"""

장점

(1) 또 다른 저장공간 없이 Hash Table 내에서 데이터 저장 및 처리가 가능하다.

(2) 또 다른 저장공간에서의 추가적인 작업이 없다.

단점

(1) Hash Function의 성능에 전체 Hash Table의 성능이 좌지우지된다.

(2) 데이터의 길이가 늘어나면 그에 해당하는 저장소를 마련해 두어야 한다.