[자료구조] 그래프 개념 (1)

1. 그래프(Graph) 란?

$G=(V,E)　where　V=Vertex, E=Edge$ 로 정의

$V(G)$ (노드 또는 정점, 공백이 아닌 유한집합)

$E(G)$ (상이한 두 Vertex(정점)를 잇는 Edge(간선), 유한집합)

---

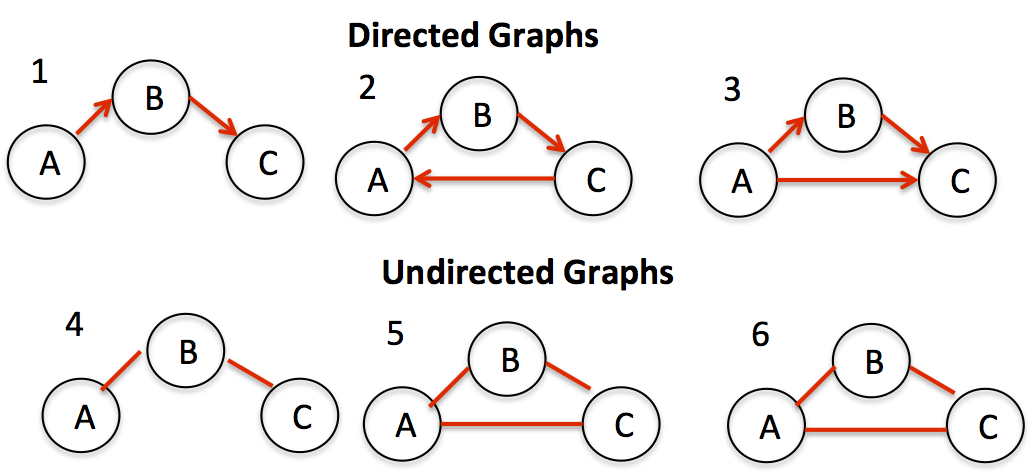
1-1. 무향 그래프, 유향 그래프

Undirected Graph (무향 그래프)

• 물리학에서 정의하는 '속력' 과 같은 개념
• Edge를 표현하는 Vertex의 쌍에서 방향(순서) 가 없는 그래프
• 두 Vertec V0 와 V1을 잇는 Edge는 '( )' 로 표현
• (V0, V1) , (V1, V0) 는 같은 Edge를 나타낸다.
  (i.e $E(V0, V1) = E(V1, V0)$)

Directed Graph (유향 그래프)

• 물리학에서 정의하는 '속도' 와 같은 개념
• Edge를 표현하는 Vertex의 쌍에서 방향(순서) 가 있는 그래프
  - 두 Vertex V0와 V1을 잇는 Edge는 '< >' 로 표현
• <V0, V1> , <V1, V0> 는 서로 다른 Edge를 나타낸다.
  (i.e $E<V0, V1> ≠ E<V1, V0>$)
  

---

1-2. 완전 그래프 (Complete graph)

• Edge(간선)을 최대한으로 가진 그래프
• 그래프 최대 Edge 수
  정점이 n개인 무방향 그래프에서 최대 간선 수: $C(n,2)=n(n-1)/2$개
  정점이 n개인 방향 그래프에서 최대 간선 수: $P(n,2)=n(n-1)$개

G5의 Edge(간선) 수:

Vertex(정점)의 개수: 4개 & 무방향 그래프
완전 그래프가 되기 위한 Edge(간선) 수: $C(4,2)=4(4-1)/2=6$개

G6의 Edge(간선) 수:

Vertex(정점) 개수:4개고 & 방향 그래프
완전 그래프가 되기 위한 Edge(간선) 수: $P(4,2)=4(4-1)=12개$

---

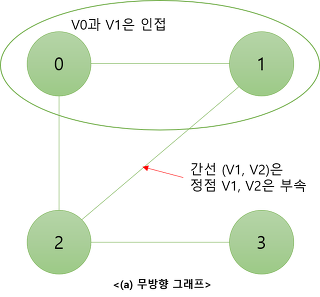
1-3. 인접(Adjacent)과 부속(Incident)

무방향 그래프의 한 간선 $(V_i, V_k)$에 대하여

• $V_j$와 $V_k$ 는 서로 인접한다.
• Edge(간선) $(V_j, V_k)$은 Vertex(정점) $V_j$와 $V_k$에 부속한다.

1-4. 부분 그래프 (Sub Graph)

G =(V,E) 를 그래프를 나타내는 함수라고 하자. 다음과 같을때 (V', E')를 G의 부분 그래프(SubGraph)라 한다.

(a) $V' ⊆ V$ 와 $E' ⊆ E$

(b) 모든 간선  $ε∈ E'$ 에 대하여  $ε$가 $v'$ 와 $w'$에 부속된다면 $v', w' ∈V'$

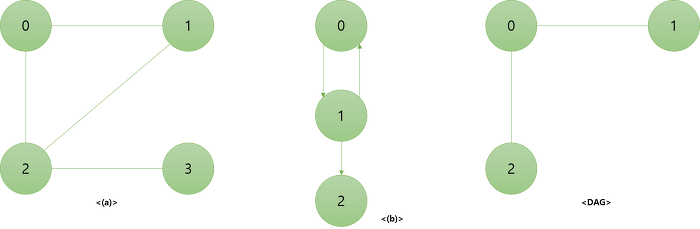
1-5. 사이클(cycle)

• 첫 번째 지점과 마지막 정점이 동일한 단순 경로
• 무방향 그래프에서 Cycle의 길이는 항상 3 이상이고, 방향 그래프에서 Cycle의 길이는 항상 2 이상이다.
• 이러한 Cycle이 없는 그래프를 DAG(Directed Acyclic Graph)라고 한다.

아래 그림은 무방향 그래프와 방향 그래프에서 사이클을 나타낸 것이다.
그림의 a 그래프는 정점 $V_0, V_1, V_2, V_0$이 사이클이며 그림 b 그래프는 정점 $V_0, V_1$이 사이클이다.

---

참조

• https://kosaf04pyh.tistory.com/131
• https://kingpodo.tistory.com/45
• https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=kimchoyoungg&logNo=220840052418