TIL 32 시간복잡도

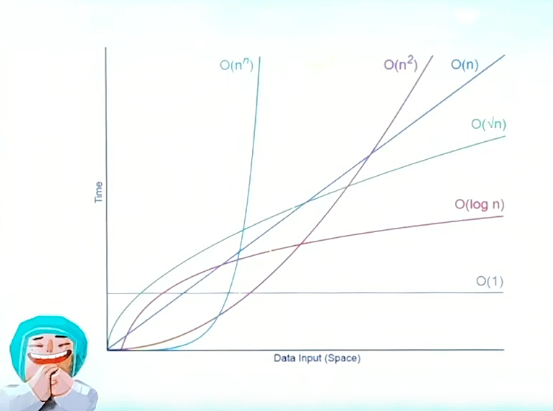
시간복잡도

문제를 해결하는데 걸리는 시간과 입력의 함수관계

빅오 표기법

핵심이 되는 연산을 찾아서 표시한다.
계산식의 가장 큰 지수를 고려하고 계수는 무시한다.

n^2 + 2n = O(n^2)
2n^4 + 3n = O(n^4)

//O(n^2)표기법
for(int i=0;i<n;i++){
  for(int j=0;j<n;j++){
  }
}
//O(n^3)이 아니라 n과 m이 무한대로가면 k는 무시할 수 있기 때문에 시간복잡도는 0이다.
for(int i=0;i<n;i++){
  for(int j=0;j<n;j++){
    for(int k=0; k<10000;k++){
    }   
  }
}
//O(logN) 갈수록 2배로 증가해서 log2n이지만 계수를 무시하고 logn이라 한다.
for(int i=1;i<n;i = i*2){
}

계산횟수가 오래걸리는 시간복잡도 : O(1) < O(logN) < O(N) < O(NlogN) < O(N^2) < O(2^N)

이진탐색

정렬된 배열에서 원하는 값을 찾는 방법

O(logN) 점점 계산횟수가 줄어듦 예시

int[] sortedArr = {1,2,3,4,5,6,7,8,9}
int mid;
int left =0
int right = sortedArr.length-1

while(right >= left){
  mid = (right + left) /2
  // 2가 배열의 왼쪽에 있다면 
  if(2 == sortedArr[mid]){
    break;
  }
  if(2<sortedArr[mid]){
    right = mid - 1
  } else {
    left = mid + 1
  }
}

O(logN) 점점 계산횟수가 줆어듦 예시

while(digit !== 0){
digit = digit/2
system.out.printin(digit)
}
}

O(N) 배열의 숫자만큼 계산 함 예시

for(let i=0;i<arr.length;i++){
if(arr[i] === 1){
  return true
}
}

시간복잡도 유형