Quick Sort
Divide and Conquer(분할 정복)을 통해서 정렬을 하는 방식입니다.
최선 또는 평균적인 케이스에서 불필요한 데이터의 이동을 줄이고 한 번 결정된 피벗들이 추후 연산에서 제외되기 때문에 다른 정렬 알고리즘에 비해서 빠르고, 정렬하고자 하는 배열 안에서 교환을 진행하기 때문에 추가적인 메모리 공간이 필요하지 않다는 장점이 있습니다.
Merge Sort와 달리 불균형 분활을 하기 때문에 정렬된 배열에서 오히려 수행 시간이 더 걸리다는 단점도 있습니다.
Divide and Conquer (분할 정복)
문제를 작은 2개로 분리하고 각각 해결하고 결과를 모아서 문제를 해결하는 방식입니다.
Code
void swap(int arr[], int index1, int index2) {
int temp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = temp;
return;
}
int partition(int arr[], int startIndex, int endIndex)
{
int pivot = arr[endIndex]; // 가장 오른쪽 값을 피벗으로 사용
int index = startIndex - 1;
for (int j = startIndex; j <= (endIndex - 1); j++) {
if (arr[j] <= pivot) {
index++;
swap(arr, j, index);
}
}
swap(arr, index + 1, endIndex);
return index + 1;
}
void quickSort(int arr[], int startIndex, int endIndex)
{
// 종료 조건
if (startIndex < endIndex)
{
// Divide
int pivot = partition(arr, startIndex, endIndex);
// Conquer
quickSort(arr, startIndex, pivot - 1);
quickSort(arr, pivot + 1, endIndex);
}
}Process
배열의 마지막 원소를 pivot으로 사용합니다. (꼭 마지막일 필요는 없습니다.)
pivot의 앞에는 더 작은 값이 뒤에는 더 큰값이 오도록 pivot을 기준으로 배열을 둘로 나눕니다.
나누면서 정렬을 하진 않으며 이 작업을 Divide(분할)이라고 합니다.
Divide가 완료된 pivot은 더 이상 움직이지 않습니다.
분할된 두 개의 배열에 대해서 재귀적으로 과정을 반복합니다.
재귀 호출이 한번 진행될 때마다 pivot의 위치들이 정렬되고 최종적으로 startIndex가 endIndex보다 커지거나 같아지기 때문에 재귀가 종료됨을 보장할 수 있습니다.
예시를 가지고 좀 더 세부적으로 보겠습니다.
[3, 1, 6, 8, 5] 의 배열이 있습니다.
int partition(int arr[], int startIndex, int endIndex)
{
int pivot = arr[endIndex]; // 가장 오른쪽 값을 피벗으로 사용
int index = startIndex - 1;
for (int j = startIndex; j <= (endIndex - 1); j++) {
if (arr[j] <= pivot) {
index++;
swap(arr, j, index);
}
}
swap(arr, index + 1, endIndex);
return index + 1;
}1 Cycle
가장 우측 값을 피벗으로 사용합니다.
startIndex = 0, endInddex = 4, pivot = 5입니다.
index는 pivot 값을 기준으로 Divide를 완료 한 뒤에 pivot의 위치를 알기 위한 index로 시작 위치(startIndex)의 -1의 위치부터 시작합니다.
j는 startIndex부터 endIndex의 직전(-1)까지 순환하면서 pivot을 기준으로 divide 할 위치를 찾습니다.
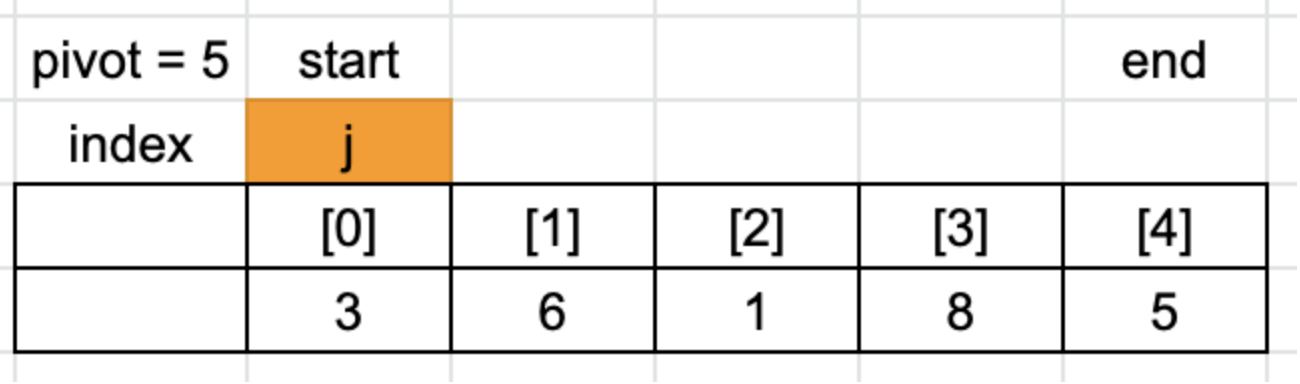
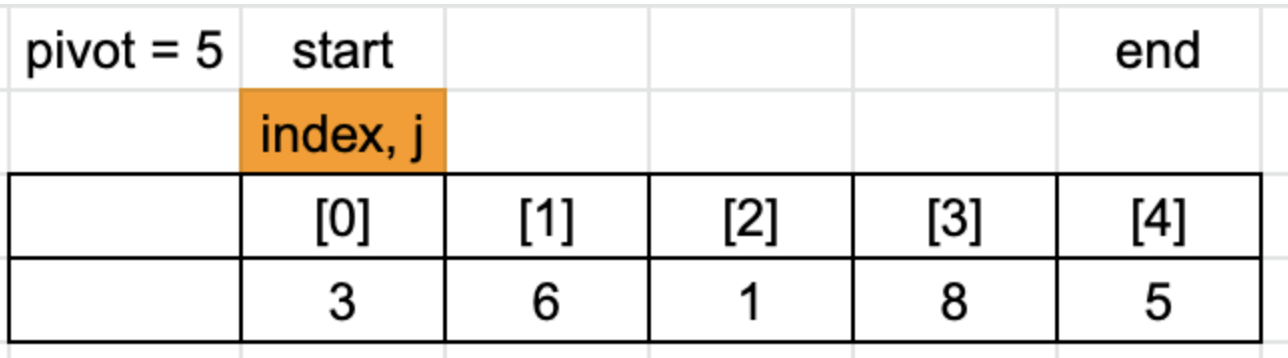
3 < 5는 true기 때문에 index의 위치를 +1 하고 인덱스가 같기 때문에 swap은 하지 않습니다.
6 < 5는 false 이기 때문에 아무 동작을 하지 않습니다.
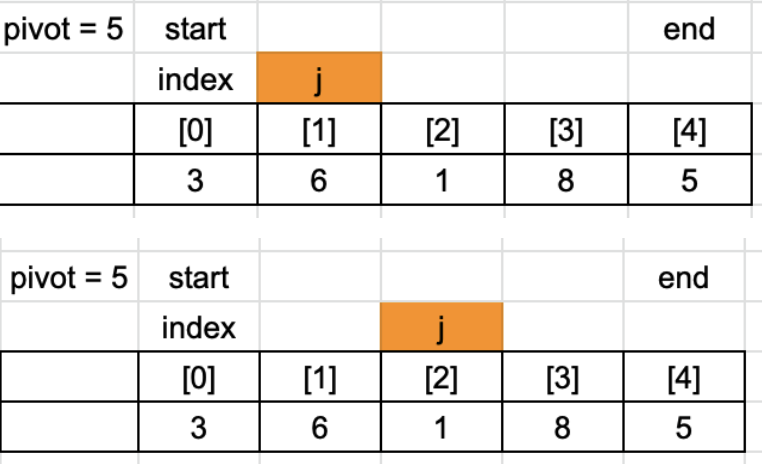
1 < 5는 true 이므로 index를 +1 합니다.
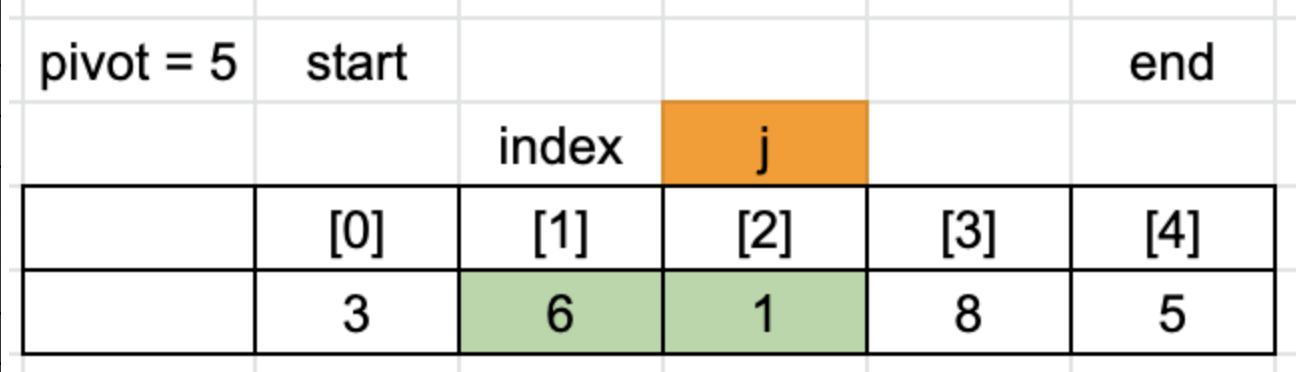
index와 j의 위치가 다르므로 값을 swap 합니다.
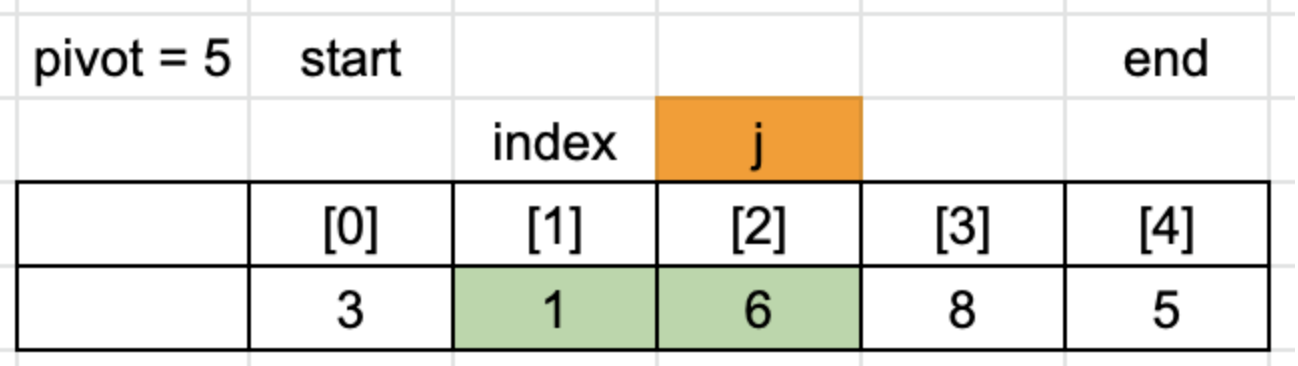
8<5는 false이므로 for문을 종료합니다.
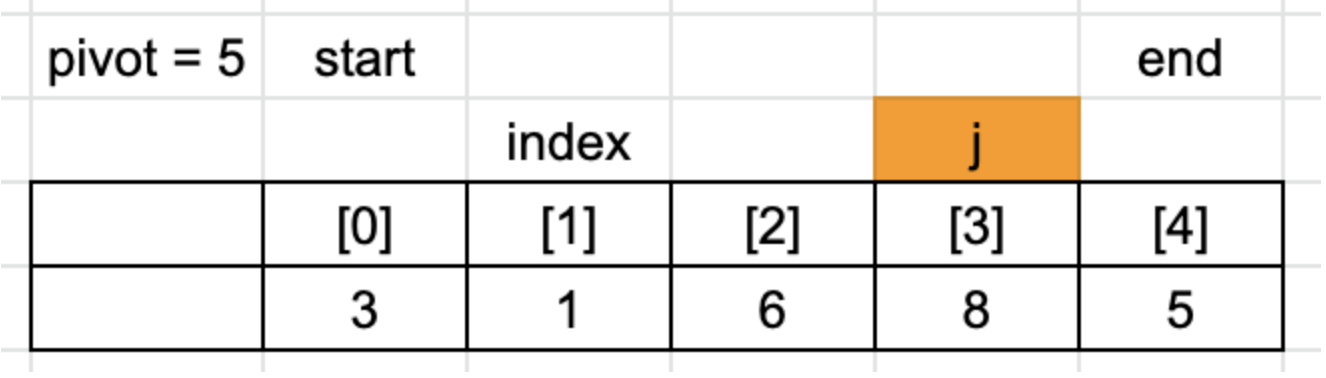
이제 index를 기준으로 왼쪽에는 pivot보다 작은 값이 오른쪽에는 pivot보다 큰 값들이 위치하고 있습니다.
이제 pivot을 제대로 된 위치로 swap 합니다.
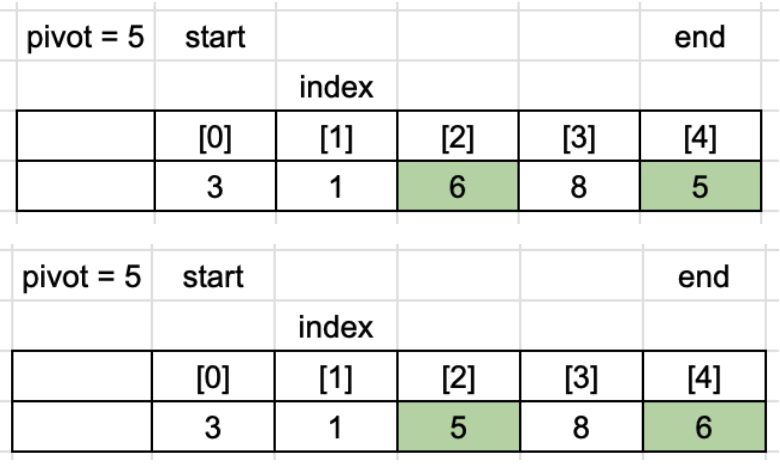
1 Cycle에서 배열은 [3, 1, 5, 8, 6]이 되며 pivot(5)의 위치는 index + 1의 값인 2가 됩니다.
void quickSort(int arr[], int startIndex, int endIndex)
{
// 종료 조건
if (startIndex < endIndex)
{
// Divide
int pivot = partition(arr, startIndex, endIndex);
// Conquer
quickSort(arr, startIndex, pivot - 1);
quickSort(arr, pivot + 1, endIndex);
}
}이제 pivot을 기준으로 왼쪽에는 작은 값이 오른쪽에는 큰 값이 위치되게 되었으므로, 배열은 2개로 나눠서 Conquer를 시작합니다. (pivot는 정렬이 완료되었다고 볼 수 있기 때문에 startIndex부터 pivot에서 하나 작은 값까지 와 pivot에서 하나 큰 값부터 endIndex까지로 나눠집니다)
2 Cycle
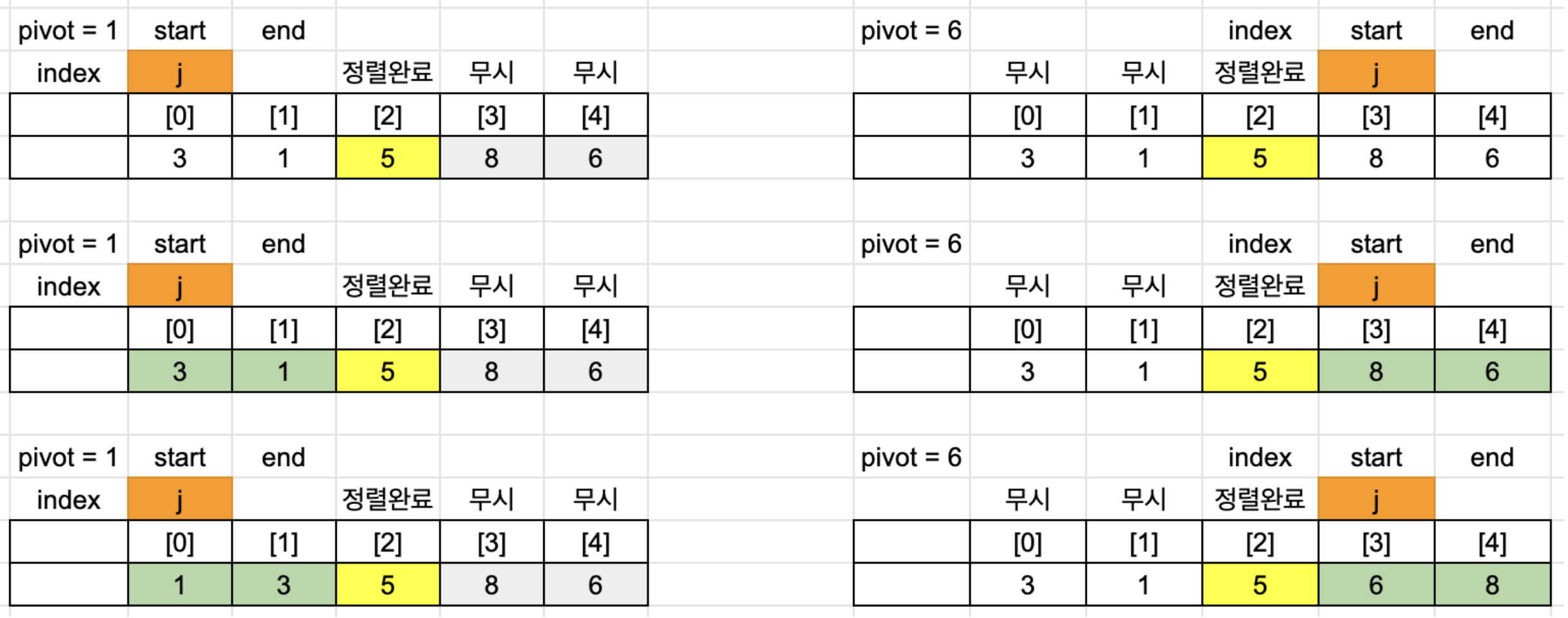
1 Cycle의 pivot의 왼쪽부터 보면,
startIndex = 0, endIndex = 1, pivot = 1, index = -1로 시작합니다.
3 < 1은 거짓이므로 for문을 종료하고, 3과 1을 swap 하고 pivot 0을 반환하고 종료합니다.
오른쪽은
startIndex = 3, endIndex = 4, pivot = 6, index = 2로 시작합니다.
8 < 6은 거짓이므로 for문을 종료하고, 8과 1을 swap하고 pivot 3을 반환하고 종료합니다.
3 Cycle
Conquer를 위해 다음 과정으로 들어가서 보니 startIndex 보다 endIndex인 이전 과정의 pivot이 더 작거나 같으므로, 재귀 호출을 끝내고 모든 함수를 반환하며 종료합니다.
결과

Time Complexity of Quick Sort
최선(Best cases), 평균(Average cases)의 경우 O(nlong)입니다.
Quick sort는 비교 횟수(순환 호출 깊이)와 각 순환 호출 단계에서의 비교 연산의 곱으로 표현할 수 있습니다.
최선, 평균의 경우 절반씩 나누면서 비교 범위를 줄여나가며 정렬을 진행하게 됩니다,
이는 정렬하고자 하는 범위 n이 2의 거듭제곱(n=2^k)라고 가정하면,
2^4의 범위는 각 사이클을 진행하면서 2^3 -> 2^2 -> 2^1 -> 2^0 만큼씩 범위가 줄어들게 됩니다.
이를 보면 k는 순환 호출되는 깊이를 나타냄을 알 수 있습니다.
log N은 2로 몇 번 나눠야 1이 될 것인가를 표현하기 때문에 k = log N임을 알 수 있고,
각 순환 호출 단계에서는 나눠진 전체 리스트를 비교하면서 진행해야 되므로 평균 n번의 비교가 이루어 짐을 알 수 있습니다.
그렇기 때문에 O(nlogn)이 됩니다.
최악(worst cases)의 경우 O(n^2)입니다.
최악의 경우는 pivot를 양 끝으로 설정하고 배열이 정렬되어 있을 경우인데, 이 경우 Divide가 이뤄지지 않아, n번만큼의 깊이를 비교해야 하고, 각 호출 단계에서 역시 평균 n번의 비교가 이루어 짐으로 O(n^2)가 됩니다.
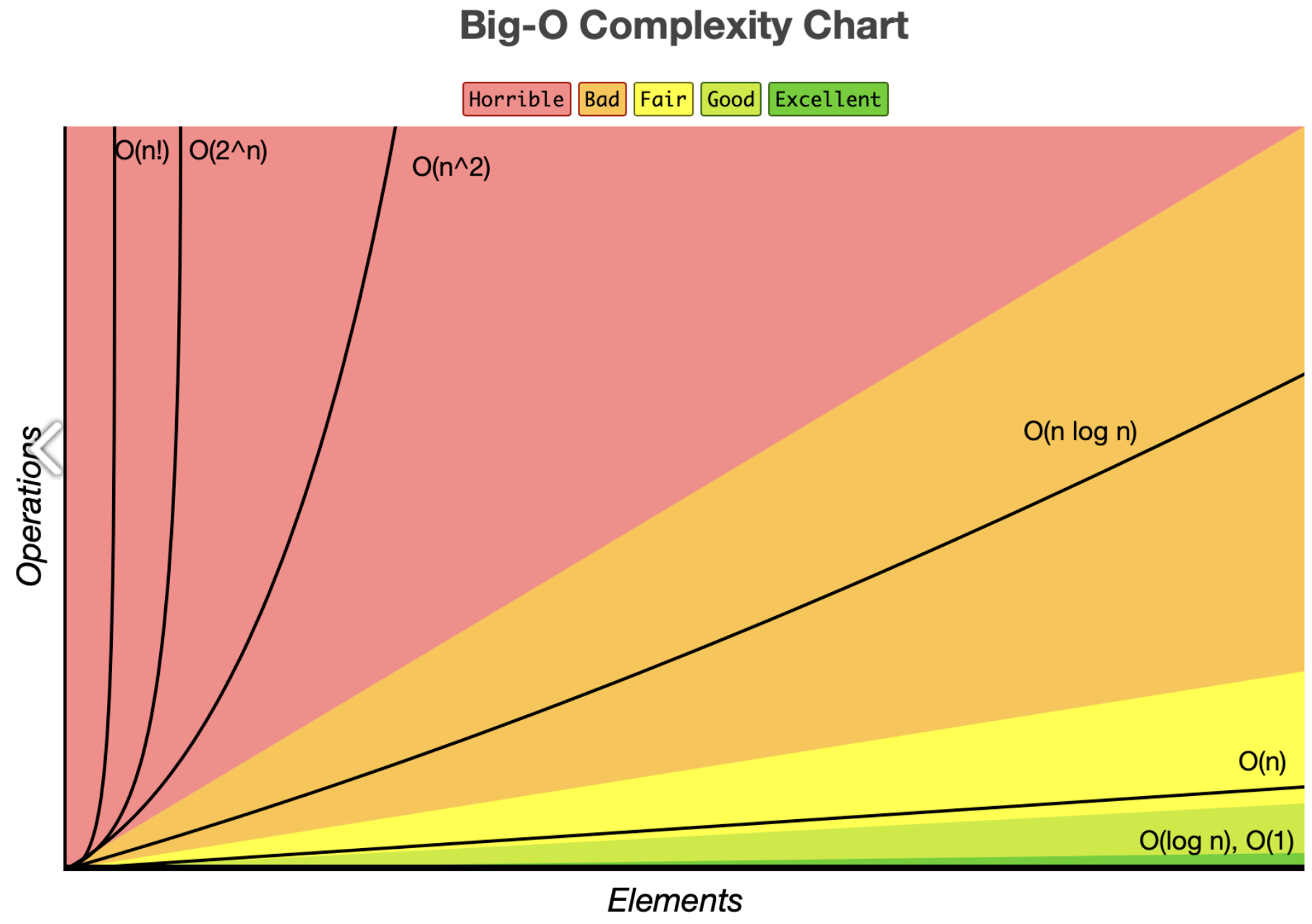
참고
https://blog.chulgil.me/algorithm/
https://www.bigocheatsheet.com