MergeSort

병합 정렬이라고 부르며 분할 정복을 통해서 정렬을 해 나아가는 방식을 말합니다. Quick Sort와는 분할 정복을 하는 것은 동일 하지만 안정 정렬에 속합니다.

안정 정렬?

퀵 정렬의 경우 피벗 값에 따라서 편향되게 분할할 가능성이 있기 때문에 최악의 경우 O(n^2) 만큼의 시간 복잡도를 가지게 됩니다. 그러나 병합 정렬은 최악의 경우에도 일정하게 반으로 나누기 때문에 O(N * logN)을 보장합니다.

---

Process

일단 반으로 나누고 나중에 합쳐서 정렬한다.

예를들어 [7, 6, 5, 8, 3, 5, 9, 1]의 배열을 합병 정렬을 해보겠습니다.
전체적인 과정은 다음과 같습니다.

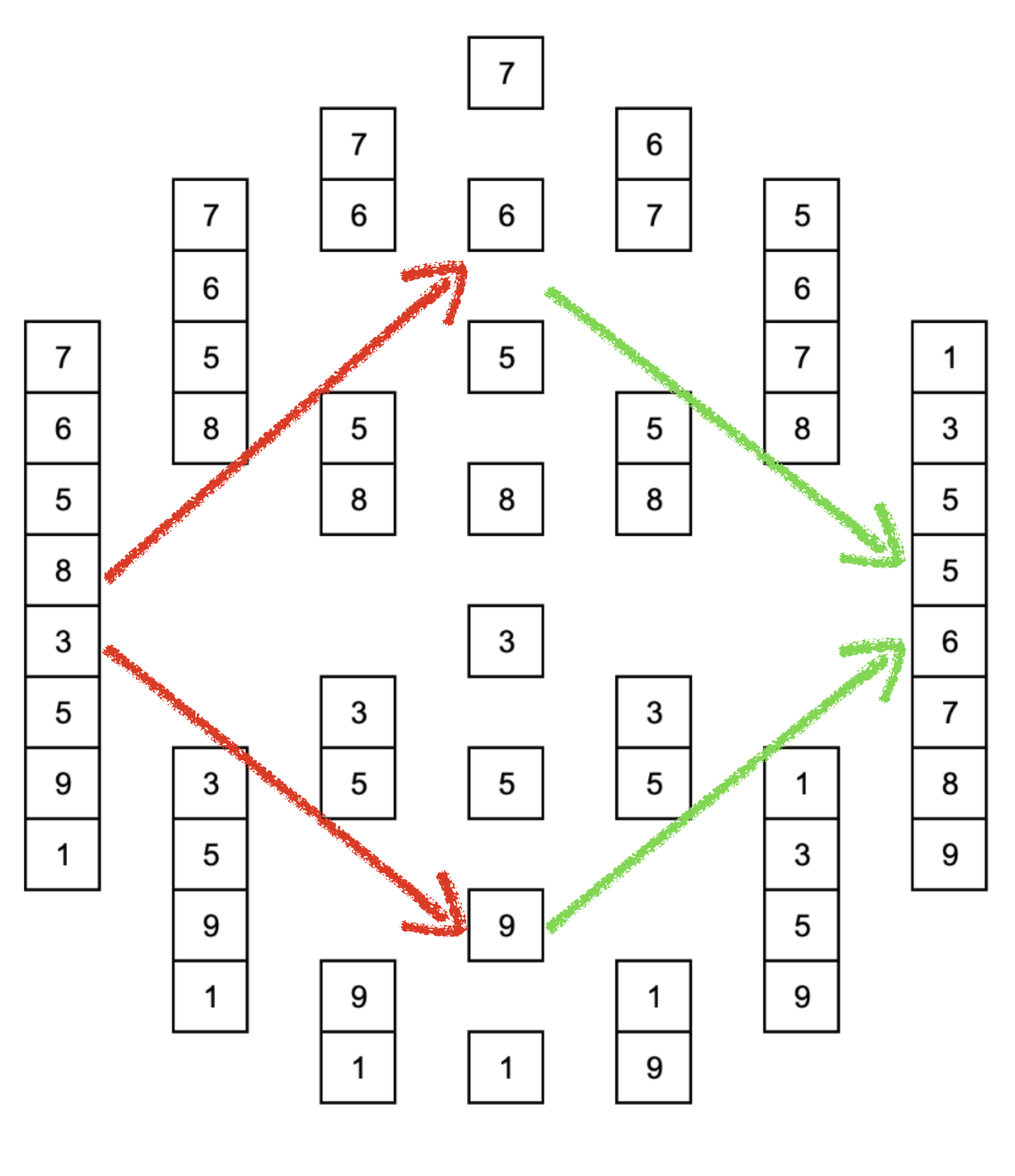
이 과정에서 알 수 있는 것은 일단 나눠질 수 없을 때까지 반으로 나누고 합치는 과정에서 각각을 정렬하고 합치 고를 반복하여 목표에 도달하는 것을 알 수 있습니다.

이제 합병정렬을 하는 과정을 하나씩 진행해보겠습니다.

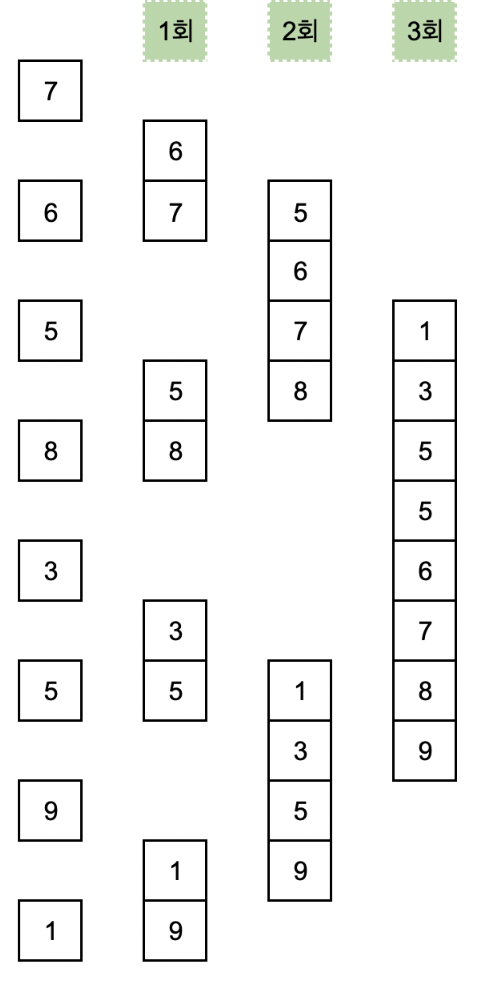
1 Cycle

위와 같이 7, 6, 5, 8, 3, 5, 9, 1을 1개의 원소씩 나눈 상태에서 1회에는 2개씩 합치면서 정렬을 진행합니다.

결과 : [6, 7] / [5, 8] / [3, 5] / [1, 9]

위와 같이 2개씩 합친 내부에서만 정렬이 되어 있습니다.

2 Cycle

4개씩 합치면서 정렬을 진행합니다.

결과 : [5, 6, 7, 8] / [1, 3, 5, 9]

여기서도 각각의 범위에서만 정렬이 되어 있음을 알 수 있습니다.

3 Cycle

8개씩 합치면서 정렬을 진행합니다.

결과 : [1, 3, 5, 5, 6, 7, 8, 9]

이제 나눈 모든 원소의 정렬이 완료되었으므로 작업을 종료합니다.

---

이게 왜 N * logN이 되는 걸까?

병합 정렬을 보면 모든 원소를 나누고 난 상태에서 2의 거듭제곱만큼의 범위를 늘려가면서 병합 정렬을 진행하는 것을 알 수 있습니다.

위의 예제를 보면 8개의 원소를 정렬하기 위해 총 3번의 과정을 거쳤다는 것을 알 수 있고, 각각의 과정을 진행하면서 2의 거듭제곱 만큼의 범위를 정렬하게 되므로 병합 정렬은 logN 번 만큼 진행을 해야 한다는 것을 알 수 있습니다.

이제 높이가 logN인건 알겠는데 왜 각각의 정렬된 배열을 합쳐서 다시 정렬된 집합을 만드는 과정이 N이 되는지를 보겠습니다.


정렬이 되는 과정을 좀 더 세부적으로 보면 다음과 같습니다.

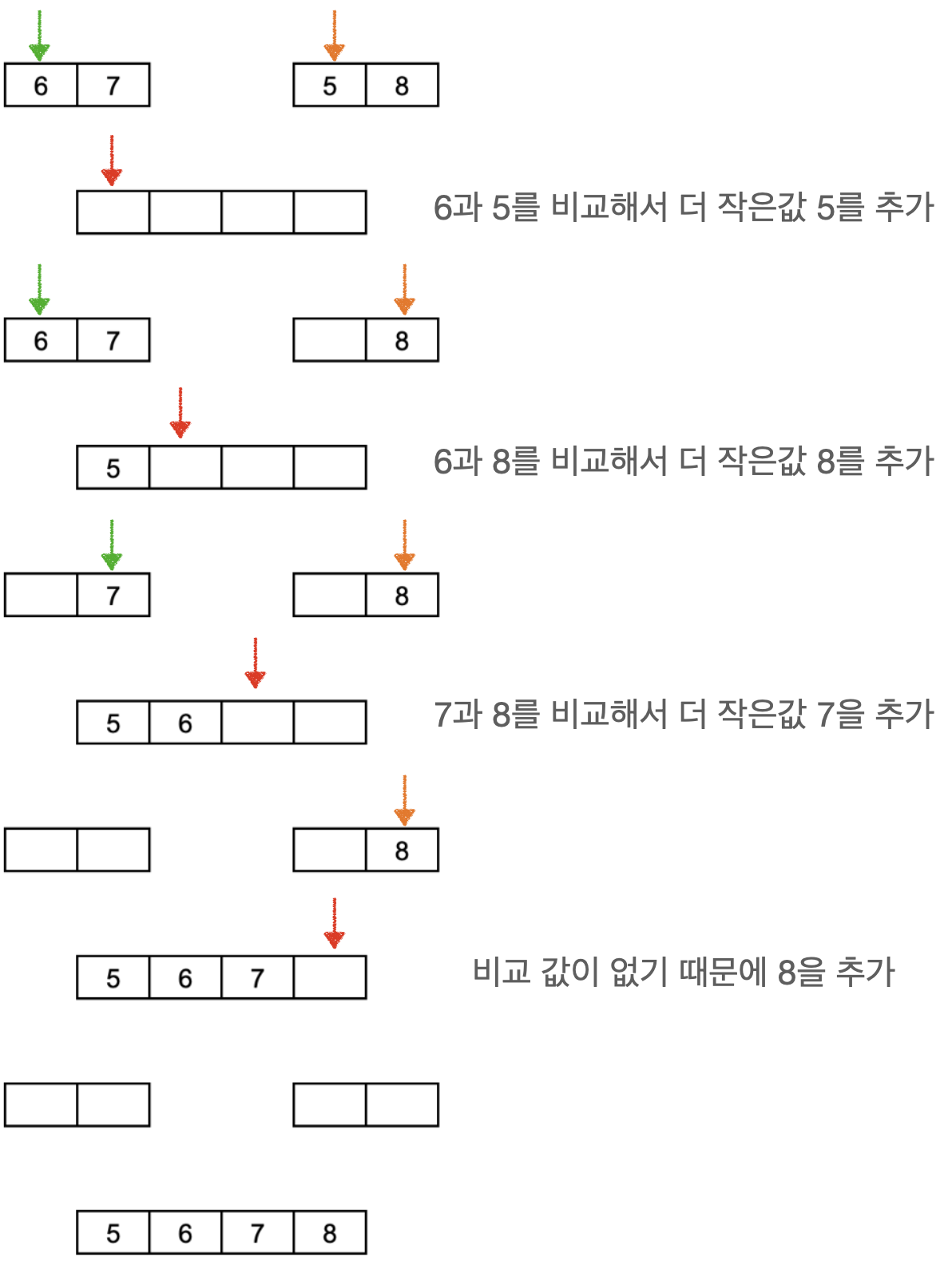
[6, 7]과 [5, 8]을 병합 정렬하는 과정에서 우선 각각의 배열이 정렬이 되어 있음을 보장할 수 있기 때문에 순차적으로 비교하면서 더 작은 값을 추가해주게 되면 전체를 순환하며 비교 값을 찾지 않아도 비교 연산 만으로 새롭게 정렬된 배열을 만들 수 있습니다. 이 과정은 원소의 개수만큼 총 N번을 수행하게 됩니다.

이와 같이 병합 정렬은 N * logN을 보장받을 수 있는 매우 빠른 정렬 방법입니다.

---

code

병합 정렬은 정렬을 수행할 때 기존의 배열외에 추가적인 배열이 필요하다는 특징이 있습니다.
매번 정렬을 수행할 때마다 새로운 배열을 생성하게 되면 불필요하게 메모리를 사용하게 되므로,
전역 변수로 정렬될 값들을 들고 있는 배열을 미리 생성하는 것이 좋다고 생각합니다.

int sorted[8];

void merge(int arr[], int startIndex, int midIndex, int endIndex) {
    int i = startIndex;
    int j = midIndex + 1;
    int k = startIndex;
    
    // 비교 후 정렬
    while (i <= midIndex && j <= endIndex) {
        if (arr[i] < arr[j]) {
            sorted[k] = arr[i];
            i++;
        }
        else {
            sorted[k] = arr[j];
            j++;
        }
        k++;
    }
    
    // 한쪽이 종료되면 나머지 값을 전부 추가한다. (이전 작업에서 정렬되어 있음을 보장)
    if (i > midIndex) {
        for (int t = j; t <= endIndex; t++) {
            sorted[k] = arr[t];
            k++;
        }
    }
    
    if (j > endIndex) {
        for (int t = i; t <= midIndex; t++) {
            sorted[k] = arr[i];
            k++;
        }
    }
    
    //  정렬된 배열 삽입
    for (int t = startIndex; t <= endIndex; t++) {
        arr[t] = sorted[t];
    }
    
}

void mergeSort(int arr[], int startIndex, int endIndex) {
    if (startIndex < endIndex) {
        int midIndex = (startIndex + endIndex) / 2;
        mergeSort(arr, startIndex, midIndex);
        mergeSort(arr, midIndex + 1, endIndex);
        merge(arr, startIndex, midIndex, endIndex);
    }
}

---

Time Complexity of Merge Sort

병합 정렬의 시간 복잡도는 O(N * logN)입니다.