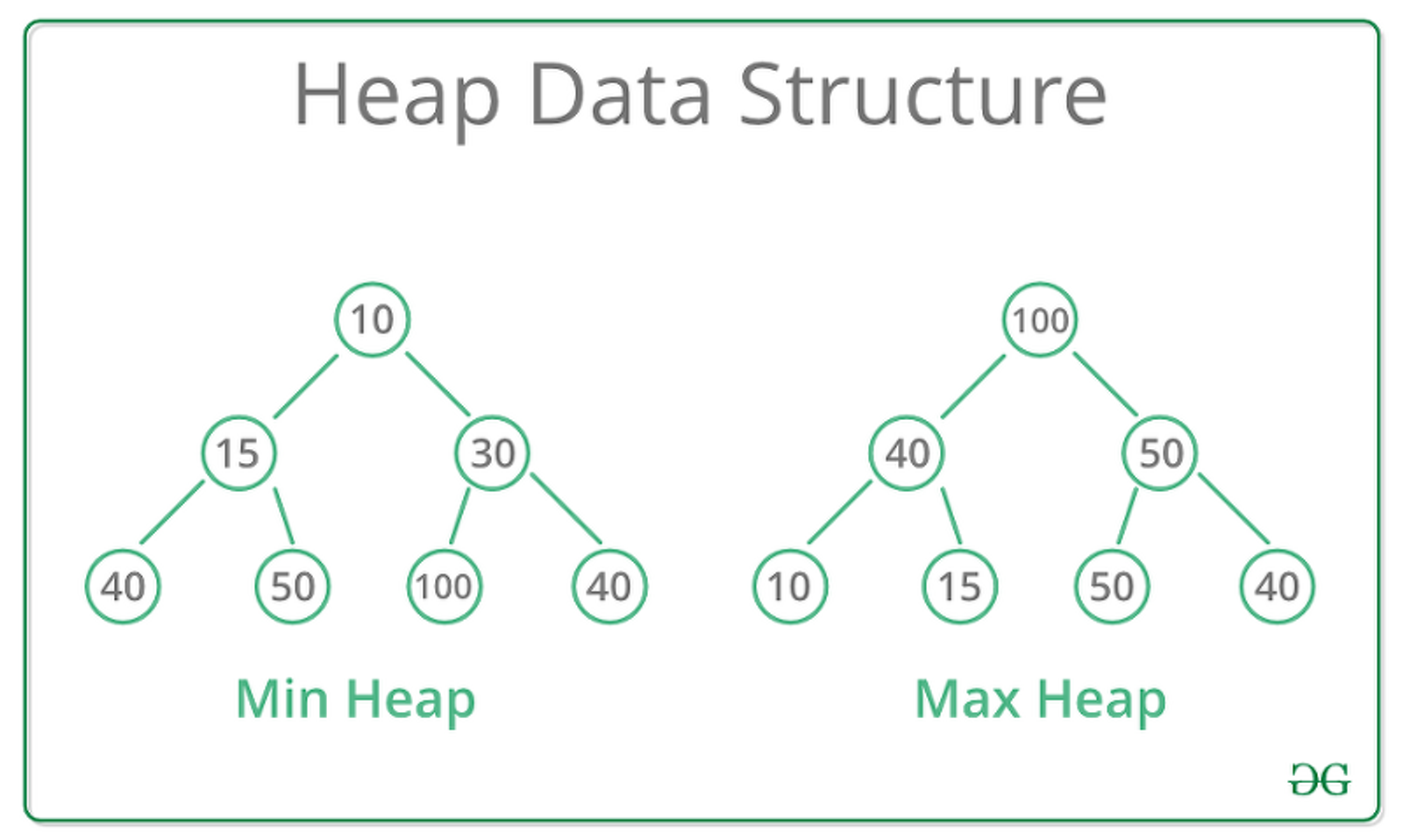
Heap
-
heapify(iterable): Converts the iterable into a heap data structure. i.e., rearranges the array to satisfy heap property. -
heappush(heap, elem): Adds an element to the heap without altering the current heap property. -
heappop(heap): Removes and returns the smallest element from the heap, ensuring that the heap property is maintained. -
heappushpop(heap, elem): Pushes a new element on the heap, then pops and returns the smallest element from the heap. The combined action runs more efficiently than heappush() followed by heappop(). -
heapreplace(heap, elem): Pops and returns the smallest element from the heap, and then pushes the new element elem. The heap size does not change. If the heap is empty, IndexError is raised. -
nlargest(n, iterable, key=None): Returns the n largest elements from the iterable. The key parameter allows specifying a function of one argument that is used to extract a comparison key from each element in the iterable. -
nsmallest(n, iterable, key=None): Returns the n smallest elements from the iterable.
Min Heap => heapq
import heapq
nums = [3, 1, 4, 1, 5, 9, 2, 6]
# Convert the list into a heap.
heapq.heapify(nums) # Heap: [1, 1, 2, 3, 5, 9, 4, 6]
# Add an element to the heap.
heapq.heappush(nums, 8) # [1, 1, 2, 3, 5, 9, 4, 6, 8]
# Pop the smallest element from the heap.
smallest = heapq.heappop(nums) # Smallest element: 1
print("After heappop:", nums) # After heappop: [1, 3, 2, 6, 5, 9, 4, 8]
# Get the three largest elements
largest_three = heapq.nlargest(3, nums) # [9, 8, 6]
# Get the three smallest elements
smallest_three = heapq.nsmallest(3, nums) # [1, 2, 3]
DFS vs BFS
NOTE:
DFS (STACK) delves deep into the graph, requiring space proportional to the maximum depth of the graph. Therefore, it consumes less space. However, it's not easy to find the shortest path.
DFS 는 탐색하는 원소를 최대한 깊게 따라가야 합니다.
이를 구현하기 위해 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고,
가장 마지막에 넣은 노드를 꺼내서 탐색하면 됩니다. → 스택!
BFS (QUEUE) can easily find the shortest path! Since it explores all branching options, it can come across all possibilities. However, as it stores all branching options, it requires more space, and since it explores all possibilities, it might take more time.
BFS 는 현재 인접한 노드 먼저 방문해야 합니다.
이걸 다시 말하면 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고,
가장 처음에 넣은 노드를 꺼내서 탐색하면 됩니다. → BFS
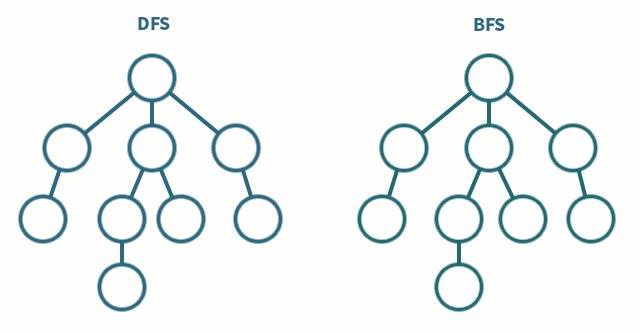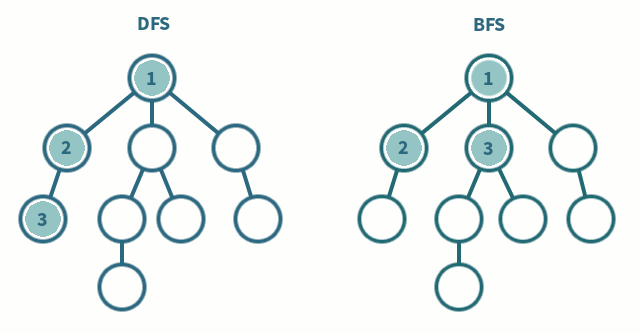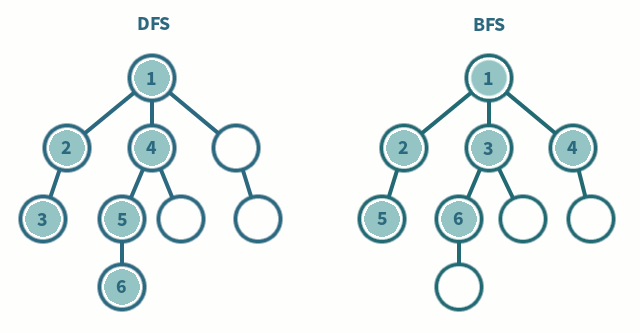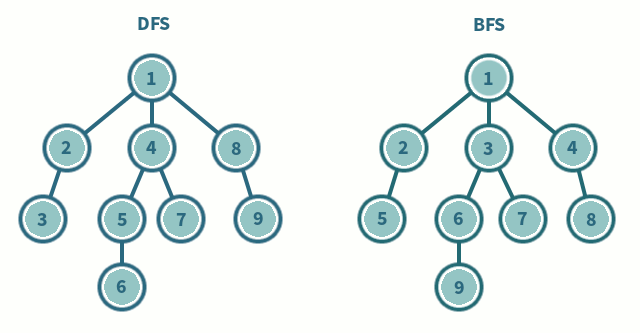
DFS
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [5, 7],
7: [6],
8: [5],
9: [1, 10],
10: [9]
}
visited = [] # 방문한 걸 저장하기 위한 배열
stack = [1] # 시작 노드인 1을 넣어둔다.
1. 현재 스택에서 가장 마지막에 넣은 1을 빼서, visited 에 추가합니다.
# stack -> [] visited -> [1]
2. 인접한 노드들인 [2, 5, 9] 에서 방문하지 않은 것들인 [2, 5, 9]를 stack 에 추가합니다.
# stack -> [2, 5, 9] visited -> [1]
3. 현재 스택에서 가장 마지막에 넣은 9을 빼서, visited 에 추가합니다.
# stack -> [2, 5] visited -> [1, 9]
4. 인접한 노드들인 [1, 10] 에서 방문하지 않은 것들인 [10] 을 stack 에 추가합니다.
# stack -> [2, 5, 10] visited -> [1, 9]
5. 현재 스택에서 가장 마지막에 넣은 10을 빼서, visited 에 추가합니다.
# stack -> [2, 5] visited -> [1, 9, 10]
6. 인접한 노드들인 [9] 에서 방문하지 않은 노드들이 없으니 추가하지 않습니다.
# stack -> [2, 5] visited -> [1, 9, 10]
7. 현재 스택에서 가장 마지막에 넣은 5를 빼서, visited 에 추가합니다.
# stack -> [2] visited -> [1, 9, 10, 5]
8. 인접한 노드들인 [1, 6, 8] 에서 방문하지 않은 것들인 [6, 8]를 stack 에 추가합니다.
# stack -> [2, 6, 8] visited -> [1, 9, 10, 5]
9. 현재 스택에서 가장 마지막에 넣은 8를 을 빼서, visited 에 추가합니다.
# stack -> [2, 6] visited -> [1, 9, 10, 5, 8]
10. 인접한 노드들인 [5] 에서 방문하지 않은 노드들이 없으니 추가하지 않습니다.
# stack -> [2, 6] visited -> [1, 9, 10, 5, 8]
11. 현재 스택에서 가장 마지막에 넣은 6을 빼서, visited 에 추가합니다.
# stack -> [2] visited -> [1, 9, 10, 5, 8, 6]
12. 인접한 노드들인 [5, 7] 에서 방문하지 않은 것들인 [7] 을 stack 에 추가합니다.
# stack -> [2, 7] visited -> [1, 9, 10, 5, 8, 6]
13. 현재 스택에서 가장 마지막에 넣은 7를 을 빼서, visited 에 추가합니다.
# stack -> [2] visited -> [1, 9, 10, 5, 8, 6, 7]
14. 인접한 노드들인 [6] 에서 방문하지 않은 노드들이 없으니 추가하지 않습니다.
# stack -> [2] visited -> [1, 9, 10, 5, 8, 6, 7]
15. 현재 스택에서 가장 마지막에 넣은 2를 빼서, visited 에 추가합니다.
# stack -> [] visited -> [1, 9, 10, 5, 8, 6, 7, 2]
16. 인접한 노드들인 [1, 3] 에서 방문하지 않은 것들인 [3] 을 stack 에 추가합니다.
# stack -> [3] visited -> [1, 9, 10, 5, 8, 6, 7, 2]
17. 현재 스택에서 가장 마지막에 넣은 3을 빼서, visited 에 추가합니다.
# stack -> [] visited -> [1, 9, 10, 5, 8, 6, 7, 2, 3]
18. 인접한 노드들인 [2, 4] 에서 방문하지 않은 것들인 [4] 를 stack 에 추가합니다.
# stack -> [4] visited -> [1, 9, 10, 5, 8, 6, 7, 2, 3, 4]
19. 현재 스택에서 가장 마지막에 넣은 4를 빼서, visited 에 추가합니다.
# stack -> [] visited -> [1, 9, 10, 5, 8, 6, 7, 2, 3, 4]
20. 인접한 노드들인 [3] 에서 방문하지 않은 노드들이 없으니 추가하지 않습니다.
21. 현재 스택에서 꺼낼 것이 없습니다. DFS 가 끝났습니다.1. 시작 노드를 스택에 넣습니다.
2. 현재 스택의 노드를 빼서 visited 에 추가한다.
3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 스택에 추가한다.
Repeat it until stack is empty (while stack)
현재 방문한 노드와 인접한 노드: adjacent_node[current_node]
방문하지 않은 걸 확인: visited
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [5, 7],
7: [6],
8: [5],
9: [1, 10],
10: [9]
}
def dfs_stack(adjacent_graph, start_node):
stack = [start_node]
visited = []
while stack:
current_node = stack.pop()
visited.append(current_node)
for adj_node in adjacent_graph[current_node]:
if adj_node not in visited:
stack.append(adj_node)
return visited
print(dfs_stack(graph, 1)) # 1 이 시작노드입니다!
# [1, 9, 10, 5, 8, 6, 7, 2, 3, 4] 이 출력되어야 합니다!BFS
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
1: [2, 3, 4],
2: [1, 5],
3: [1, 6, 7],
4: [1, 8],
5: [2, 9],
6: [3, 10],
7: [3],
8: [4],
9: [5],
10: [6]
}
visited = [] # 방문한 걸 저장하기 위한 배열
queue = [1] # 시작 노드인 1을 넣어둔다.
1. 현재 큐에서 가장 처음에 넣은 1을 빼서, visited 에 추가합니다.
# queue -> [] visited -> [1]
2. 인접한 노드들인 [2, 3, 4] 에서 방문하지 않은 것들인 [2, 3, 4]를 queue 에 추가합니다.
# queue -> [2, 3, 4] visited -> [1]
3. 현재 큐에서 가장 처음에 넣은 2을 빼서, visited 에 추가합니다.
# queue -> [3, 4] visited -> [1, 2]
4. 인접한 노드들인 [1, 5] 에서 방문하지 않은 것들인 [5]를 queue 에 추가합니다.
# queue -> [3, 4, 5] visited -> [1, 2]
5. 현재 큐에서 가장 처음에 넣은 3을 빼서, visited 에 추가합니다.
# queue -> [4, 5] visited -> [1, 2, 3]
6. 인접한 노드들인 [1, 6, 7] 에서 방문하지 않은 것들인 [6, 7]를 queue 에 추가합니다.
# queue -> [4, 5, 6, 7] visited -> [1, 2, 3]
7. 현재 큐에서 가장 처음에 넣은 4을 빼서, visited 에 추가합니다.
# queue -> [5, 6, 7] visited -> [1, 2, 3, 4]
8. 인접한 노드들인 [1, 8] 에서 방문하지 않은 것들인 [8]를 queue 에 추가합니다.
# queue -> [5, 6, 7, 8] visited -> [1, 2, 3, 4]
9. 현재 큐에서 가장 처음에 넣은 5을 빼서, visited 에 추가합니다.
# queue -> [6, 7, 8] visited -> [1, 2, 3, 4, 5]
10. 인접한 노드들인 [2, 9] 에서 방문하지 않은 것들인 [9]를 queue 에 추가합니다.
# queue -> [6, 7, 8, 9] visited -> [1, 2, 3, 4, 5]
11. 현재 큐에서 가장 처음에 넣은 6을 빼서, visited 에 추가합니다.
# queue -> [7, 8, 9] visited -> [1, 2, 3, 4, 5, 6]
12. 인접한 노드들인 [3, 10] 에서 방문하지 않은 것들인 [10]를 queue 에 추가합니다.
# queue -> [7, 8, 9, 10] visited -> [1, 2, 3, 4, 5, 6]
13. 현재 큐에서 가장 처음에 넣은 7을 빼서, visited 에 추가합니다.
# queue -> [8, 9, 10] visited -> [1, 2, 3, 4, 5, 6, 7]
14. 인접한 노드들인 [3] 에서 방문하지 않은 것들이 없으니 추가하지 않습니다.
# queue -> [8, 9, 10] visited -> [1, 2, 3, 4, 5, 6, 7]
15. 현재 큐에서 가장 처음에 넣은 8을 빼서, visited 에 추가합니다.
# queue -> [9, 10] visited -> [1, 2, 3, 4, 5, 6, 7, 8]
16. 인접한 노드들인 [4] 에서 방문하지 않은 것들이 없으니 추가하지 않습니다.
# queue -> [9, 10] visited -> [1, 2, 3, 4, 5, 6, 7, 8]
17. 현재 큐에서 가장 처음에 넣은 9을 빼서, visited 에 추가합니다.
# queue -> [10] visited -> [1, 2, 3, 4, 5, 6, 7, 8, 9]
18. 인접한 노드들인 [5] 에서 방문하지 않은 것들이 없으니 추가하지 않습니다.
# queue -> [10] visited -> [1, 2, 3, 4, 5, 6, 7, 8, 9]
19. 현재 큐에서 가장 처음에 넣은 10을 빼서, visited 에 추가합니다.
# queue -> [] visited -> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
20. 인접한 노드들인 [6] 에서 방문하지 않은 것들이 없으니 추가하지 않습니다.
# queue -> [] visited -> [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
21. 현재 큐에서 꺼낼 것이 없습니다. BFS 가 끝났습니다.
1. 시작 노드를 큐에 넣습니다.
2. 현재 큐의 노드를 빼서 visited 에 추가합니다.
3. 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가한다.
Repeat until queue is empty (while queue)
현재 방문한 노드와 인접한 노드: adjacent_node[current_node]
방문하지 않은 걸 확인: visited# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
1: [2, 3, 4],
2: [1, 5],
3: [1, 6, 7],
4: [1, 8],
5: [2, 9],
6: [3, 10],
7: [3],
8: [4],
9: [5],
10: [6]
}
def bfs_queue(adj_graph, start_node):
queue = [start_node]
visited = []
while queue:
current_node = queue.pop(0)
visited.append(current_node)
for adj_node in adj_graph[current_node]:
if adj_node not in visited:
queue.append(adj_node)
return visited
print(bfs_queue(graph, 1)) # 1 이 시작노드입니다!
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 출력되어야 합니다!