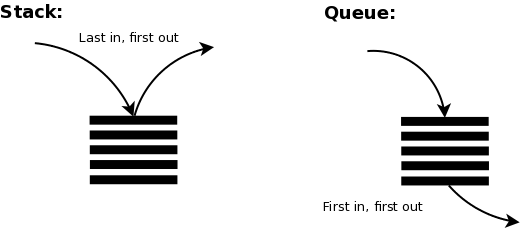
Stack & Queue

bomi ·2024년 4월 5일

algorithm

목록 보기

2/6

Stack

STACK = Last In First Out (LIFO) = "LIST"

stack = []            # 빈 스택 초기화
stack.append(4)       # 스택 push(4)
stack.append(3)       # 스택 push(3)
top = stack.pop()     # 스택 pop
print(top)            # 3!

Q1.

Q. 수평 직선에 탑 N대를 세웠습니다. 모든 탑의 꼭대기에는 신호를 송/수신하는 장치를 설치했습니다. 
발사한 신호는 신호를 보낸 탑보다 높은 탑에서만 수신합니다. 
또한 ,한 번 수신된 신호는 다른 탑으로 송신되지 않습니다.

예를 들어 높이가 6, 9, 5, 7, 4 인 다섯 탑이 왼쪽으로 동시에 레이저 신호를 발사합니다. 
그러면, 탑은 다음과 같이 신호를 주고 받습니다. 

높이가 4인 다섯 번째 탑에서 발사한 신호는 높이가 7인 네 번째 탑에서 수신하고, 
높이가 7인 네 번째 탑의 신호는 높이가 9인 두 번째 탑이, 
높이가 5인 세 번째 탑의 신호도 높이가 9인 두 번째 탑이 수신합니다. 

높이가 9인 두 번째 탑과 높이가 6인 첫 번째 탑이 보낸 레이저 신호는 
어떤 탑에서도 수신할 수 없습니다.

이 때, 맨 왼쪽부터 순서대로 탑의 높이를 담은 배열 heights가 매개변수로 주어질 때 각 탑이 쏜 신호를 어느 탑에서 받았는지 기록한 배열을 반환하시오.

[6, 9, 5, 7, 4] # 라고 입력된다면,

# 아래 그림처럼 탑이 있다고 보시면 됩니다!
<- <- <- <- <- 레이저의 방향
   I 
   I
   I     I
I  I     I
I  I  I  I  
I  I  I  I  I
I  I  I  I  I
I  I  I  I  I
I  I  I  I  I

[0, 0, 2, 2, 4] # 다음과 같이 반환하시면 됩니다!

A.
top_heights = [6, 9, 5, 7, 4]


def get_receiver_top_orders(heights):
    answer = [0] * len(heights)
    while heights:
        height = heights.pop()
        for idx in range(len(heights) - 1, -1, -1):
            if heights[idx] > height:
                answer[len(heights)] = idx + 1
                break
    return answer


print(get_receiver_top_orders(top_heights))  # [0, 0, 2, 2, 4] 가 반환되어야 한다!

print("정답 = [0, 0, 2, 2, 4] / 현재 풀이 값 = ",get_receiver_top_orders([6,9,5,7,4]))
print("정답 = [0, 0, 0, 3, 3, 3, 6] / 현재 풀이 값 = ",get_receiver_top_orders([3,9,9,3,5,7,2]))
print("정답 = [0, 0, 2, 0, 0, 5, 6] / 현재 풀이 값 = ",get_receiver_top_orders([1,5,3,6,7,6,5]))

NOTE
idx in range(len(heights) - 1, -1, -1):

Q2.

Q. 스택 수열

1부터 n까지의 수를 스택에 넣었다가 뽑아 늘어놓음으로써, 하나의 수열을 만들 수 있다. 
이때, 스택에 push하는 순서는 반드시 오름차순을 지키도록 한다고 하자. 
임의의 수열이 주어졌을 때 스택을 이용해 그 수열을 만들 수 있는지 없는지, 있다면 어떤 순서로 push와 pop 연산을 수행해야 하는지를 알아낼 수 있다. 
이를 계산하는 프로그램을 작성하라.

A. 
def stack_sequence(n, sequence):
    stack = []
    result = []
    sequence_idx = 0
    num = 1
    
    while sequence_idx < n :
        if stack and sequence[sequence_idx] == stack[-1]:
            stack.pop()
            sequence_idx += 1
            result.append("-")
        
        elif num <= n:
            stack.append(num)
            num += 1
            result.append("+")
        
        else:
            # If it's impossible.
            return "NO"
        
        # Avoid infinite loops
        if num > n + 1:
            break

    return result

# sequence = list()
# n = int(input())
# for _ in range(n):
#     sequence.append(int(input()))

n = 8  
sequence = [4, 3, 6, 8, 7, 5, 2, 1]  
print(stack_sequence(n, sequence))

Q3.

Q. 괄호가 바르게 짝지어졌다는 것은 '(' 문자로 열렸으면 반드시 짝지어서 ')' 문자로 닫혀야 한다는 뜻이다. 예를 들어

()() 또는 (())() 는 올바르다.
)()( 또는 (()( 는 올바르지 않다.

이 때, '(' 또는 ')' 로만 이루어진 문자열 s가 주어졌을 때, 문자열 s가 올바른 괄호이면 True 를 반환하고 아니라면 False 를 반환하시오.

A. 
def is_correct_parenthesis(string):
    stack = []

    for i in range(len(string)):
        if string[i] == "(":
            stack.append("(")
        elif string[i] == ")":
            if stack and stack[-1] == "(":
                stack.pop()
            elif not stack:
                return False
    if stack:
        return False
    return True


print("정답 = True / 현재 풀이 값 = ", is_correct_parenthesis("(())"))
print("정답 = False / 현재 풀이 값 = ", is_correct_parenthesis(")"))
print("정답 = False / 현재 풀이 값 = ", is_correct_parenthesis("((())))"))
print("정답 = False / 현재 풀이 값 = ", is_correct_parenthesis("())()"))
print("정답 = False / 현재 풀이 값 = ", is_correct_parenthesis("((())"))

Queue

QUEUE = First In First Out (FIFO) = "deque"

NOTE
You can use list for Queue as you did in Stack.
However, it is not efficent so you use 'deque'(double-ended queue)

deque has popleft() method, which deletes the first data ~ (list.pop(0))
deque has appendleft(x) method, which inserts data to the front ~ (list.insert(0, x))

Reference: https://www.daleseo.com/python-queue/

from collections import deque

queue = deque([4, 5, 6])
queue.append(7)
queue.append(8)
queue
>>> deque([4, 5, 6, 7, 8])
queue.popleft()
>>> 4
queue.popleft()
>>> 5
queue
>>> deque([6, 7, 8])

queue_2 = deque([4, 5, 6])
queue_2.appendleft(3)
queue_2.appendleft(2)
queue_2
>>> deque([2, 3, 4, 5, 6])
queue_2.pop()
>>> 6
queue_2.pop()
>>> 5
queue_2
>>> deque([2, 3, 4])

Q. Description
초 단위로 기록된 주식가격이 담긴 배열 prices가 매개변수로 주어질 때, 가격이 떨어지지 않은 기간은 몇 초인지를 return 하도록 solution 함수를 완성하세요.

제한사항
prices의 각 가격은 1 이상 10,000 이하인 자연수입니다.
prices의 길이는 2 이상 100,000 이하입니다.

입출력 예
prices	return
[1, 2, 3, 2, 3]	[4, 3, 1, 1, 0]

입출력 예 설명
1초 시점의 ₩1은 끝까지 가격이 떨어지지 않았습니다.
2초 시점의 ₩2은 끝까지 가격이 떨어지지 않았습니다.
3초 시점의 ₩3은 1초뒤에 가격이 떨어집니다. 따라서 1초간 가격이 떨어지지 않은 것으로 봅니다.
4초 시점의 ₩2은 1초간 가격이 떨어지지 않았습니다.
5초 시점의 ₩3은 0초간 가격이 떨어지지 않았습니다.

A.
from collections import deque

def solution(prices):
    answer = []
    prices = deque(prices)
    
    while prices:
        num_non_drop = 0    
        current_price = prices.popleft()    
    
        for next_prices in prices:
            # case 1: drop 하지 않았을때
            if current_price <= next_prices:
                num_non_drop += 1
            # case 2: drop 했을때
            else:
                num_non_drop += 1
                break
                
        answer.append(num_drop)
    return answer

Stack vs Queue

Use a Stack when:

Last-In-First-Out (LIFO) Structure is Needed: A stack follows the LIFO principle, where the last element added to the stack is the first one to be removed. This is useful in scenarios where you need to reverse things or backtrack from the last step.

Depth-First Search (DFS): In graph or tree traversals, stacks are used to explore as far as possible along a branch before backtracking, which is the essence of DFS.

Backtracking Problems: For solving puzzles or searching through a problem space (like in the case of maze puzzles, combination problems, or parsing expressions), where you might need to backtrack to the previous state.

Call Stack Simulation: To simulate recursive function calls or to keep track of previous function calls (like in the case of evaluating an expression or implementing recursion without actual recursive function calls).

String Manipulation: Stacks are helpful in several string manipulation problems, such as checking for balanced parentheses or reversing a string.

Use a Queue when:

First-In-First-Out (FIFO) Structure is Needed: A queue follows the FIFO principle, where the first element added is the first to be removed. This is ideal for scenarios where things need to be processed in the same order they were added.

Breadth-First Search (BFS): In graph or tree traversals, queues are used to explore the neighbors of a node before moving on to the next level, which is characteristic of BFS.

Scheduling Algorithms: For implementing scheduling, especially in operating systems where processes are scheduled in the order they arrive (like in CPU or IO scheduling).

Buffer or Cache Implementations: Queues can be used to manage data buffers that process data at different rates, such as in networking where packets arrive at a pace that might not match the processing rate.

Level Order Traversal in Trees: To traverse a tree level by level, where you process all nodes at one level before moving to the next.

Choosing Between Stack and Queue:

Analyze the Order of Operations:

Determine if your problem requires processing the most recent element first (use a stack) or processing elements in the order they were added (use a queue).