11. NP-Complete problems

glow.soon·2022년 2월 16일

목록 보기

12/12

지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다

13. NP-Complete problems

class P, class NP, class NPC가 있음
누군가 open problem 제시, P=NP?

problems and algorithms

각 문제마다 고유의 complexity 가짐, 문제의complexity는 그 문제를 해결하는 가장 좋은 알고리즘의 complexity이다
가장 좋다는 의미는 현존하는 알고리즘에서 좋다는것이 아닌, 가능한 모든 알고리즘들 중에서 좋다는 것을 의미
앞으로 나타날수도 알고리즘 까지 포함해서 이 알고리즘보다 더 빠를 수 없다는 best 알고리즘에 대한 complexity가 문제의 복잡도라고 할수 있음

Optimization Problems Vs. Decision Problems

Optimization Problems
- 다양한 솔루션 존재 할수있지만 가장 좋은 솔루션 찾는 문제
- ex. shortest-path문제
Decision Problems (결정 문제)
- yes or no
- PATH : 그래프 주어지고 yes or no 로 대답할수있는 정수 k 주어짐-> k 기준으로 k edges만큼 갈수 있는 path존재 하는가?

Polynomial Time: Class P

Polynomial time에 수행 할수있는 문제 정의

T(n)=O(n^k)
ex. O(n^3logn), O(n^4)

어떤 문제(decision problem)가 polynomial time 알고리즘이 존재한다면 그런 문제들을 class P 라고 부름

그런 알고리즘들은 efficient하다고 볼것임, 문제에 대해서는 easy하다고 표현

Some Problems are Very Hard

어떤 문제들은 Polynomial Time에해결하는 법 찾지 못했음
대표적으로 0/1 knapsack problem, traveling salesperson problem(TSP)가 있음

0/1 knapsack problem(->NPC)
동굴에 n개의 보물(item)이 있다.
ith item은 Vi dollars 와 Wi 무게를 갖는다(Vi, Wi는 양수)
가방에 W(integer)무게만큼 담을수 있을때, 도둑은 가능한 비싼 물건(optimization problem)을 담길 원한다. 어느 item을 가져가야 할까?
이때 k 이상의 이득이 되도록 담을 조합이 있는가?-> decision problem
(단, 도둑은 각 item을 가져가든기 가져가지 않아야함, item의 일부분 가져갈수 없음, 한번이상 가져갈수 없음)
* Fractional Knapsack problem
->item의 일부분 가져갈수 있음 (다항시간에 해결가능)
traveling salesperson problem(TSP)(->NPC)
complete weighted graph가 주어졌을때, 1. 최소비용(optimization problem)으로 모든 vertex를 한번씩만 방문하는 cycle은? 2. cycle의 weight k이하로 -> decision problem)
* Euler tour problem
connected digraph 주어졌을때 모든 edge를 한번씩만 방문하는 cycle 존재하는가?
(다항시간에 해결가능 O(m) time)
Undecidable problems : 결정 할수 없는 문제 즉, 컴퓨터로 해결할수 없는 문제 (turing machine 정지 or 무한루프 될것인가)

Dealing with Hard Problems

Polynomial Time 알고리즘을 찾을수 없었을때, 나만 못찾은것이 아닌 다른사람들도 마찬가지로 모두가 어려워하는 문제라 아직 Polynomial Time 알고리즘 찾을수 없다!!!!! -> NP Complete 문제 증명하는 방법

Non-Deterministic Polynomial Time: Class NP

non-determinitstic하다를 의미 (deterministic이란 용어는 오토마타 분야에서 옴)

DFA : deterministic finite automata
NFA : Non-deterministic finite automata
- determiistic: 하나의 입력(state)에서 하나의 transition (다음상태) 결정 되있는 상태
- non-deterministic : 같은 입력에서 알고리즘이 다르게 수행되는 경우

따라서 그 문제를 해결하는 non-deterministic polynomial-time algorithm 존재한다면 그런 decision problem을 class NP라고 함

다른 정의 방식: 어떤 certificate(근거)가 주어지면 그것을 polynomial time에 검증할수 있어야함 (우리는 이것으로 정의할것)

P의 문제는 NP의 부분집합이기도 하다 (P⊆NP)
open problem (P=NP, P!=NP->아직 증명못함)
많은 연구자들은 P와 NP는 다를것이라고 믿고 있음

NP Example

certificate	output of verification algorithm
참	yes
거짓	...(대답할수없음, no output)

ex) UFO가 존재할것인가, 존재 하지않는가?
누군가 UFO가 있다고 말하면서, 사진이나 동영상 공개(certificate)->근거가 참이면 UFO 존재한다고 할 수 있음, but 근거가 거짓이라고해서 UFO가 존재하지 않는다고 확실히 말할 수 없음(no output)

문제: 입력으로 그래프 주어졌을때 weight K이하인 MST 존재하는가? (yes or no)
검증 알고리즘
1. certificate y 주어짐(n-1개의 edge로 구성된 집합 T)
2. T가 spanning tree의 모양을 갖는가?
3. T의 weight가 K이하인가? -> 다항시간에 보여주기, 가능하면 yes 아니면 no output
테스트 하는데 O(n+m) time 소요, 따라서 이 알고리즘은 다항시간에 검증가능->class NP
class P : the class of decision problems that are polynomially bounded (다항시간에 해결되는 문제를 의미)
class NP : the class of decision problems for which there is a polynomially bounded non-deterministic algorithm (다항시간에 검증할수 있는 decision problem의 집합을 의미)

The class NP-Complete

어떤 문제 Q가 NP-hard이다-> class NP에 있는 어떤 문제에 대해, 그 문제만큼은 어려운 문제
- class NP에 있는 어떤 문제를 문제 Q로 reducible 할수 있으면 된다 (reduction: 축소변환)
ex) 문제 P(최대값 찾기 문제)를 문제 Q(정렬문제)로 reducible 할수 있다 (문제 Q를 해결 할수 있으면 P도 해결할수 있다는 소리)--> 정렬 문제가 적어도 최대값 찾기 문제만큼은 어렵다고 할 수 있다 (이런 방식이 NP-hard 증명 방법)
어떤 문제 Q가 NP-complete이다 -> 이 문제가 만약 class NP이고 NP-hard이면 그 문제를 NP-complete라 함

따라서 어떤 문제 만났을때 NP-complete 증명하려면 두가지 (NP, NP-hard) 증명 해야함
NP-hard를 증명하는 것은 reducible하다라는것을 보이면 됨 -> NP hard임을 증명하고 싶은 문제를 문제 Q로 놓고, 기존에 알려져있는 NP-complete문제를 문제 P로 놓으면 됨
즉, 우리의 문제를 가지고 기존에 알려져 있는 문제(NP-complete)를 해결할수 있음을 보이면 됨

Polynomial reductions

문제 P에 대한 input을 문제 Q에 대한 input으로 다항시간에 변환할수 있음을 보여야함, 그 함수를 reduction function이라 함(다항시간에 변할수 있음을 보이기)

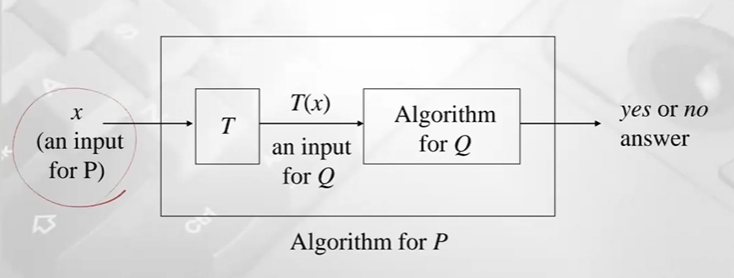
P를 우리의 문제 Q(NP-hard임을 증명하고 싶은 문제)로 해결할수 있음을 보이기

input x (기존에 알려진 문제 P)

다항시간에 문제 P에 대한 input을 문제 Q에대한 input으로 변할 수 있음을 증명(transformation function T)
T(x): 문제 Q에대한 input으로 바뀐 것 의미
이것에 대해 문제 Q를 해결한다면 문제 Q에서 나온 output이 완전하게 문제 P의 output과 동일하다는것을 보이면 됨, 즉 문제 Q에 대한 output이 yes이면 항상 문제 P에서도 yes임을 보이고, 문제 Q에서 output이 no이면 항상 문제 P에서도 no가 된다는것을 증명

P <= pQ (p: 다항시간에 reduction됨을 의미, <=: 문제 Q가 적어도 문제 P만큼은 어렵다 의미)

example

P : Hamiltonian-cycle problem : given a graph G, is there a cycle in G that visits each vertex exactly once?(그냥 그래프 주어졌을때, 모든 vertex한번씩 방문하는 cycle 존재하는가?, 이미 NPC라고 증명 되있음)
Q : Traveling-salesperson problem : given a complete weighted graph G, is there a cycle in G that visits each vertex exactly once and has total cost at worst K?

Problem Q가 NPC임을 증명
1. class NP
(input, certificate)가 주어졌을때, 다항시간에 검증 할 수 있음을 보인다
certificate로 n개의 edge가 주어지면, n개의 edge를 따라가면서
1. 각 vertex를 한번씩만 방문하는 cycle인지 확인
2. edge들의 weight의 sum이 K이하인지 확인
-> O(n) time에 검증 할 수있다(polynomial time)
결과는 yes or no-output
검증은 완료

NP hard
1) transformation
문제 P의 input G,(x)라고 하고 transformation func 거쳐 TSP문제의 input으로 변환 할것
기존의 edge들은 weight를 0으로 초기화 해주고 complete그래프 이기 때문에 없던 edge들은 weight를 1로 초기화해줌, input으로 K주어져야 하기 때문에 K=0으로 만들어줌

이렇게 변환하는것 다항시간에 할 수있다.
(complete 그래프는 edge수가 많아야 O(n^2)에 bound되기때문에 input을 O(n^2)에 transformation 할 수 있다)

2) TSP문제의 output과 H.C의 output이 항상 일치함을 보이기
- TSP의 출력이 yes -> H.C출력 yes 보이기
  ->K를 0으로 했기 때문에 K이하인 H.C이 존재한다면 그것은 그 edge들의 집합은 모두 weight가 0인 것만 지나가야함
  그 즉슨, H.C의 input에서 기존에 존재했던 edge들만 지나가는 H.C이 존재한다는것을 의미.
  따라서 TSP문제에서 weight가 0인 H.C이 존재한다는것은 원래 H.C문제에서의 H.C이 존재한다는것과 일치
- TSP의 출력이 no -> H.C 출력 no 보이기
  ->만약 문제의 해를 계산하는데 해가 존재 하지 않는다는것은 K=0인 H.C이 TSP문제에 없다는것 의미. 적어도 한번이라도 weight가 1인 edge를 지나 가야한다는 것을 의미 즉 기존에 G에서 기존의 edge만으로는 H.C이 존재할수 없다는것을 의미
  따라서 TSP문제의 input에서 H.C의 K=0인 H.C이 존재하지 않는다면, 그래프 G에서 H.C에서도 존재할수 없음
  
  (두문제의 output 일치)

따라서 TSP 문제는 class NP이면서 NP-hard이기 때문에 NP-Complete이다

어떤 문제가 NP-hard 증명하기 위해선 반드시 기존에 증명된 NP-hard or NPC문제 존재해야함. 즉 기존에 증명된 NPC문제 이용해서 계속 NPC문제들이 탄생할수 있음 (transitive한 관계 가짐) 이렇게 하려면 최초의 NPC문제 가지고 있어야함 그것이 무엇일까?

CIRCUIT-SAT

최초의 NP Complete 문제

0 또는 1의 값을 가진 n개의 boolean값 input으로 주어짐

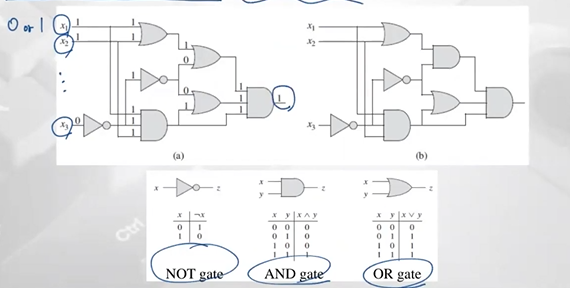
최종 출력이 1이 되는 input의 조합이 존재하는가?
(total 나올수있는 경우의 수: 2^n가지)
다항시간에 해결하는것은 쉽지않음, 아직까지 다항시간에 해결하는 방법 찾지 못함 (이 문제들로부터 점점 많은 NPC 문제 증명했음, 모든 NPC 문제들 circuit-sat문제로 reduction 가능)

Some NP-Complete problems

SET-COVER
ex) S={{1,2,3},{2,4},{3,4},{4,5}} |S|=m
U={1,2,3,4,5} |U|=n
Decision problem: k보다 적은수에 set을 union하여 U를 생성할수 있는가?
(해=>{1,2,3},{4,5})
총 부분집합은 2^m의 경우의수를 가지고 예시에선 쉬워 보이지만 n,m 이 충분히 커지면 다항시간에 찾기 쉽지않음

(optimization problem-가장 적은 수의 set을 union하여 U를 만들수 있는 집합은)
- VERTEX-COVER (기존의 NPC문제)에 의해 NPC 문제임을 증명
SUBSET-SUM
n개의 정수로된 집합 주어지고 {v1,v2,v3...vn}, 정수 k가 주어짐, 집합 원소들의 합이 정확히 k와 같은 부분집합 존재하는가?

2^n개의 subset가지고, 다항시간에 해결하기 쉽지 않음

(optimization problem-원소의 합이 k보다 작으면서 가장 큰값을 가지는 부분집합은?)
- VERTEX-COVER (기존의 NPC문제)에 의해 NPC 문제임을 증명
0/1 Knapsack
input으로 n개의 item이 주어지고, 각 item마다 무게와 가치가 주어짐 가방의 무게가 W이하 이면서 이익이 적어도 K인 item들의 집합이 존재하는가?
(optimization problem-가장 이익이 되는 조합은?)
- SUBSET-SUM (기존의 NPC문제)에 의해 NPC 문제임을 증명
Hamiltonian-cycle
그래프 G가 주어지면 모든 vertex를 한번만 방문하는 사이클 존재하는가?
- VERTEX-COVER (기존의 NPC문제)에 의해 NPC 문제임을 증명
  (optimization problem-TSP 문제로 간주함)
Traveling saleperson tour
입력으로 complete weighted graph G가 주어지고 weight가 K이하인 헤밀토니안 사이클 존재하는가?
(optimization problem-weight가 최소인 헤밀토니안 사이클은?)

SAT

유명한 NPC 문제
각각 0또는 1로 구성된 boolean 변수 주어지고, 허용된 연산은 or, and, not 연산
ex) (a+b+¬d+e)(¬a+¬c)(¬b+c+d+e)(a+¬c+¬e)
(정의: 항 하나하나를 literal이라고 부름, 괄호안의 수식: clause, 전체수식: CNF)

CNF가 주어졌을때 결과를 1로 만드는 input의 조합이 존재하는가?

clause의 조합 0또는 1로 주어지면 O(nm) time에 검증 가능 (CIRCUIT-SAT문제에 의해 NPC라고 증명됨)

3SAT

모든 clause를 3개 literal로 제한
ex) (a+b+¬d)(¬a+¬c+e)(¬b+d+e)(a+¬c+¬e)
(2SAT문제는 다항시간에 해결가능), SAT문제에 의해 NPC라고 증명됨

Vertex Cover

input으로 그래프가 주어지고, k개 이내에 모든 vertex를 cover하는 정점 집합 존재하는가? (vertex cover: 정점들의 부분집합으로, 그래프의 모든 edge들은 vertex cover의 정점중 하나 이상에 인접하는것)

(optimization problem-최소크기의 vertex cover 찾기)

O(n^2) edges - 다항시간에 검증가능(class NP)
3SAT문제에 의해 NPC라고 증명됨

Undirected Hamiltonain cycle NPC임을 증명하기

P: Directed Hamiltonian cycle (기존에 NPC라 증명)
Q: Undirected Hamiltonain cycle

Q가 NPC임을 증명하자

Class NP임을 보이기
undirected graph 주어지고 누군가 certificate 제시할것임, 어떤 path를 제시했을때 그 path가 1. vertex를 한번씩만 방문하는가, 2.Hamiltonain cycle인지 다항시간에 검증하면 됨
만나는 edge의 수 O(n^2)으로 bound될 것이고 이는 즉, O(n^2)에 검증 가능할 것이다
(yes이면 yes, no이면 no-output)
NP-hard임을 보이기
1. transformation
  문제 P의 input을 G라고 하면
  
  다항시간에 문제 Q의 input으로 transform할수 있음을 보이자
  모든 vertex들을 먼저 triple로 생성해주고 각각 연결시킴, 그다음 G에서 directed edge가 있으면 3번째 vertex에서 1번째 vertex로 가는 edge하나 생성해줌
  
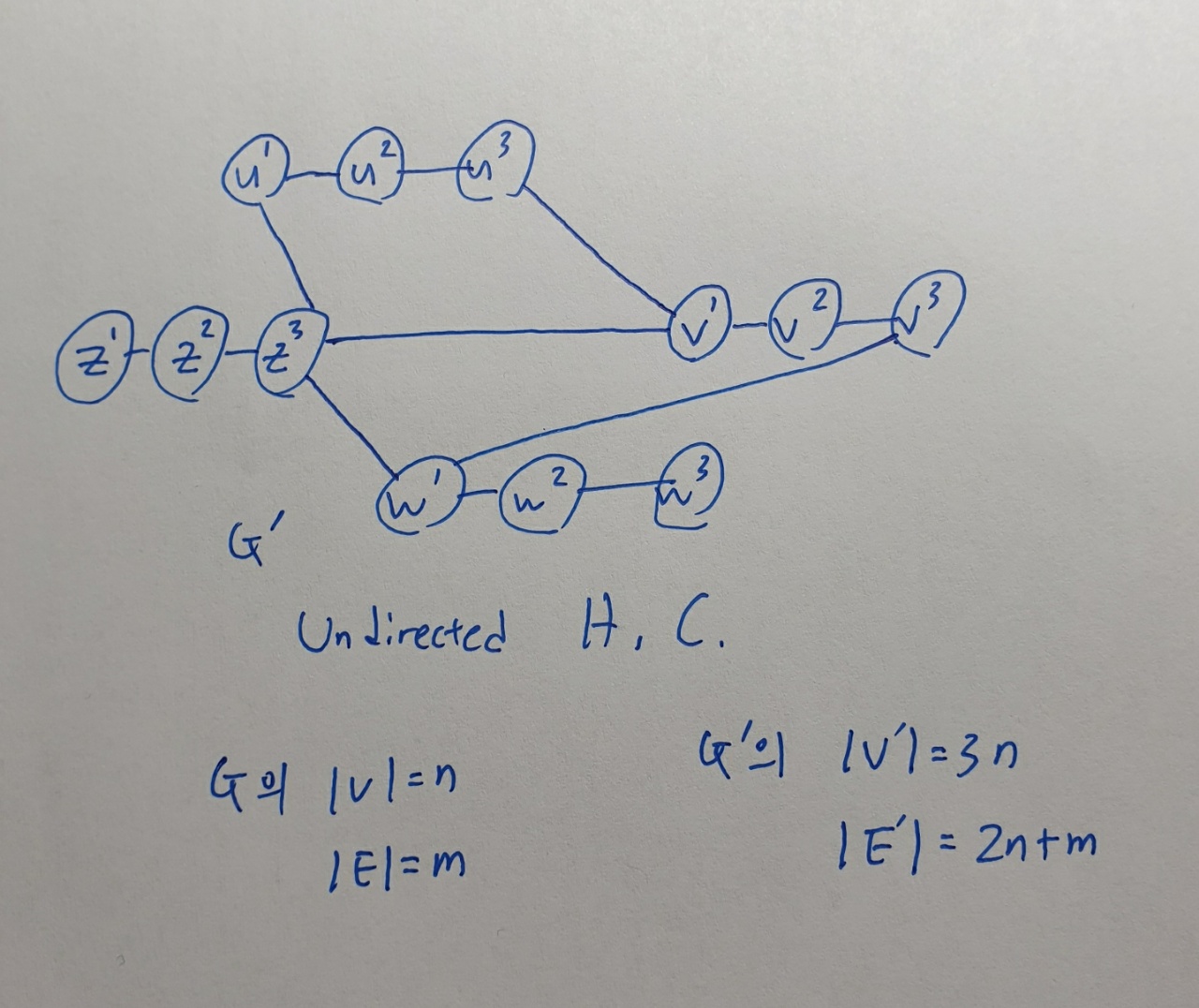
  따라서 G와 G'의 vertex개수와 edge개수의 관계에 의해 입력 G를 G`로 변환하는데 O(n+m) time에 변환 가능하다
2. Undirected Hamiltonain cycle의 output과 Directed Hamiltonian cycle의 output이 항상 일치함을 보이기
  - yes -> yes임을 보이기
    G'에서 edge가 다 undirected 그래프이기 때문에 방향이 1,2,3->1,2,3 or 3,2,1->3,2,1 이렇게 진행 할 것임
    만약 1,2,3 으로 진행한다면 G에서도 똑같은 순서로 방향을 가지게 됨 따라서 G'에서 1,2,3 순서로 가고 H.C.가 존재한다면 G에서도 H.C.이 존재하게 됨 (역순에서도 존재 할 수 있음(3,2,1 존재 한다는것은 거꾸로 1,2,3도 존재함을 의미))
    따라서 yes -> yes를 증명가능
  - no -> no 임을 보이기
    대우를 이용해서 증명 할수 있음 (Directed Hamiltonian cycle의 output이 yes이면 Undirected Hamiltonain cycle의 output도 yes이다)
    G의 H.C.가 <v1,v2,....,vn>으로 존재 한다면 G`에서는 <v1^1, v1^2, v1^3, v2^1, v2^2, v2^3....vn^1, vn^2, vn^3> 으로 존재 할 수 밖에 없다 (그래프의 모양 때문에)
    따라서 no -> no를 증명 가능
    그러므로 Undirected Hamiltonain cycle은 NP-hard이다