10. 문자열 매칭 (KMP 알고리즘, 보이어 무어 알고리즘)

glow.soon·2022년 2월 14일
알고리즘
0

알고리즘

목록 보기
11/12

지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다

11. String Matching

Pattern matching이라고도 부름

  • input으로 긴 스트링인 text T와
    상대적으로 짧은 스트링인 pattern P 주어짐
  • T에서 P가 발생하는 위치 찾는 문제 -> String matching

Strings

  • string=characters의 나열

    • c++ 프로그램
    • html 문서
    • DNA 염기서열
    • Digitized 이미지

  • alphabet Σ =스트링 구성하는 문자집합 의미

    • ASCII
    • {0,1} // binary alphabet
    • {A,C,G,T} // DNA alphabet

  • 하나의 스트링을 P라고 정의하고, 그 사이즈를 m이라 정의하자

    • substring(부분문자열)-임의의 인덱스 i부터 j까지 연속된 char의미

    • prefix(접두사)-substring of p[0..i]

    • suffix(접미사)-substring of p[i.. m-1]

      Example

    • 응용분야-텍스트 에디터, 검색 엔진, 생물학 연구

Brute-Force Algorithm

단순하게 모든 경우에 대해 수행하기

  • T와 P간의 비교연산
  • Text 왼쪽부터 패턴 탐색, 모든 pattern과 T의 Substring 일치하는것 발견할때까지 
Algorithm BruteForceMatch(T, P)
    Input text T of size n and pattern
    P of size m
    Output starting index of a substring of T equal to P
    or -1 if no such substring exists

    for i <- 0 to n - m{ test shift i of the pattern } //n-m까지 탐색진행, i=text상 인덱스
        j <- 0 //j=pattern상의 인덱스
        while j < m and T[i + j] = P[j]
            j <- j + 1
        if j = m
            return i {match at i}
    return -1 {no match anywhere}
  • 시간복잡도 O(nm)
  • worst case 예
    • T=aaa...ah
    • P=aaah (m번 비교)
    • n개의 위치에서 m번 비교할수 있음
    • 이미지 파일이나 DNA 염기에서 가끔 발생
    • 일반 텍스트에서는 거의 발생 X

The KMP algorithm

브루트 포스 알고리즘에 비해 더 shift 할 수 없을까?

  • 왼쪽부터 오른쪽으로 비교해가다가 mismatch 발생하면 패턴을 얼만큼 shift 할 수 있을까 즉 가장 멀리 뛸수있는게 어딜까 생각 해 볼수 있음
  • 중복되는 비교연산 피하기위해 패턴을 얼만큼 이동 시킬까
  • 가장 긴 j번쨰 prefix와 suffix를 가지고 비교하기

idea

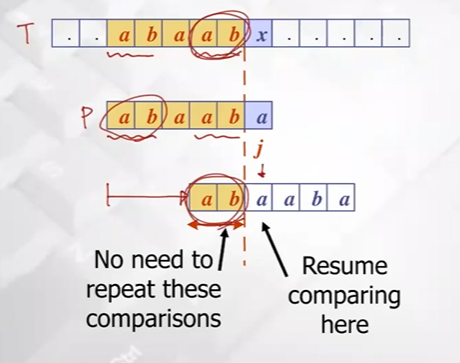
지금까지 match 되었던 prefix안에서 일치하는 최장 proper prefix 정보와 proper suffix정보 이용

  • 길이 1인 proper prefix, proper suffix -> a, b -> mismatch
  • 길이 2인 proper prefix, proper suffix -> ab, ab -> match
  • 길이 3인 proper prefix, proper suffix -> aba, aab -> mismatch ...

즉 패턴 내에서 가장 일치하는 proper prefix, proper suffix 정보는 ab, 이정보를 가지고 패턴을 멀리 shift할것

proper prefix(ab)와 text상의 ab를 align 시킴

KMP Failure Function

패턴 preprocessing 하는 failure func먼저 계산해주어야함

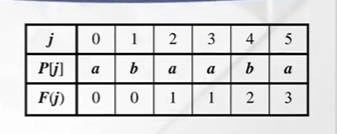
첫번째 의미: 패턴의 index를 j라 했을때 j까지 prefix내에서 일치하는 가장 긴 prefix와 proper suffix의 길이를 저장 (길이 m인 array 하나로 계산가능 O(m))

  • F(0): index 0 내에 일치하는 최대 proper prefix, proper suffix 길이 저장, but a에서 proper prefix, proper suffix는 empty string 밖에 없음 따라서 F(0)은 무조건 0
  • F(1): a, b 비교 -> 다름 -> 0 저장
  • F(2): 길이 1인 prefix, suffix 비교 (a,a) -> 일치, ab, ba 불일치 -> 최종 1 저장
  • F(3): a, a 일치, ab, aa 불일치, aba, baa 불일치 -> 최종 1 저장
  • F(4): a, b 불일치, ab, ab 일치, aba, aab 불일치, abaa, baab 불일치 -> 최종 길이 2 저장
  • F(5): a, a 일치, ab ba 불일치, aba, aba 일치, abaa, aaba 불일치, abaab, baaba 불일치-> 가장 길게 일치하는 길이 3 저장

두번째 의미: 다음에 비교할 pattern의 index를 의미 (단, index가 0 based일때)

지금까지 match된 정보를 가지고 failure func이용

  • index 4까지 일치
  • f(4) 이용!! (2 저장되있는 상태)
  • 패턴이 shift하고 나서 다음에 비교할 char의 인덱스가 2라는 것 의미 -> 인덱스 2에 있는 값으로 다음 비교

정리: j=0에서 mismatch 발생한경우 brute-force,
j>0이면 failure func 이용

Algorithm KMPMatch(T, P)
    F <- failureFunction(P) // O(m) time
    i <- 0 // text의 인덱스
    j <- 0 // pattern의 인덱스
    while i < n
        //match 부분
        if T[i] = P[j]
            if j = m - 1
                return i - j { match }
            i <- i + 1
            j <- j + 1
        //
        //mismatch 부분
        else if j > 0
            j <- F[j - 1] // failure func이용
        else //j=0일때 (브루트 포스)
            i <- i + 1
        //
    return -1 { no match }
  • i 증가하는 case 최대 n까지 증가가능
  • i 가만히 있는부분(mismatch)에서 추가적 loop실행 -> 패턴 많아야 n번 shift 가능
  • 총 while loop의 worst case = 2n을 넘지 않음
  • 따라서 KMP 알고리즘의 총 수행시간 O(m+n)

Computing the Failure function

Algorithm failureFunction(P) // O(m) time에 계산 가능
    F[0] <- 0
    i <- 1
    j <- 0
    while i < m
        if P[i] = P[j]
            {we have matched j + 1 chars}
            F[i] <- j + 1
            i <- i + 1
            j <- j + 1
        else if j > 0
            {use failure function to shift P}
            j <- F[j - 1]
        else
            F[i] <- 0 { no match }
            i <- i + 1
  • while loop 2m 넘을수 없음

F(j) 구하기 example

Example

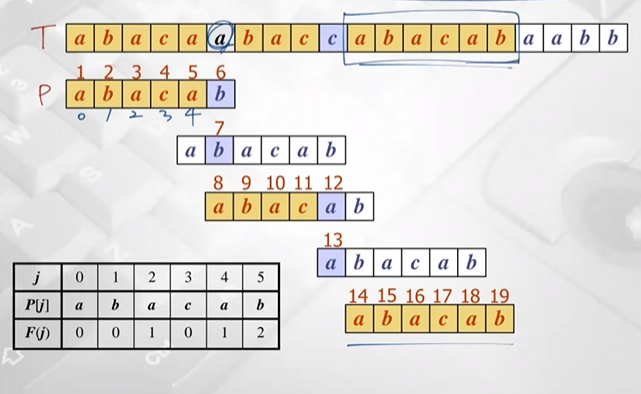
  • 처음 b에서 mismatch
  • 직전 index 4 -> F(4) 확인 : 1
  • 다음 패턴 index 1 에 맞춰줌
  • a, b 불일치 -> F(0) 확인 : 0
  • 다음패턴 index 0 에 맞춰줌
  • c, a 불일치
  • 직전 index 3 -> F(3) 확인 : 0
  • 다음패턴 index 0 에 맞춰줌
  • c, a 또 불일치 (j=0)
  • brute-force 실행
  • 패턴 일치

19번의 비교연산으로 탐색 완료

Boyer-Moore Heurisitics

두가지 Heuristics 전략 사용 알고리즘

Heuristics-어떤 알고리즘이 Heuristics이라 하는것은 최적해를 찾는것인데 그중에서 global optimal solution이 있고, local optimal solution이 있음
global optimal solution은 전체 input에 대해 최적해를 찾는것이고, local optimal solution은 전체적으로는 최적이 아닐수 있지만, 최적에 가까운 지역적으로는 최적의 solution 찾는 방법이 있음.
그중에 Heuristics 알고리즘은 global optimal solution 찾는데 굉장히 오랜시간 걸릴 수 있고 빠른시간에 local optimal solution 계산 보장하는 알고리즘 - Heuristics 알고리즘
(global opimal solution 보장하지 않지만 빠른시간에 global에 가까운 optimal solution 계산해줄수 있다.)

  1. Looking-glass (거꾸로의, 반대의) heuristic : pattern의 오른쪽부터 왼쪽으로 비교
  2. Character-jump heuristic: mismatch 발생한경우 text에 char을 기준으로 그 char가 패턴에서 마지막으로 발생한 위치가 어디인지를 살펴 보는 것 (더 앞에있다면, 그 위치가 align되도록 패턴을 shift해줌), 어떤 text에 char가 패턴에는 존재하지 않는다면 (bad character) 그 다음 index에 align 하도록 점프 많이해줌

example

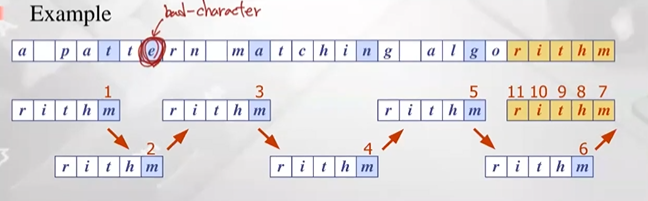
어떤 char가 존재하는지 존재하지 않는지 해당 char가 마지막에 발생 위치어디인지 미리 preprocessing 해줘야함 -> Last-occurrence function

Last-occurrence function

Σ= {a, b, c, d}, P = abacab라면 그것에 대한 string은 a,b,c,d로만 이뤄져야함
Last-occurrence function의 크기->|Σ|=s

  • 처음에 모든 data -1로 초기화
  • index 0에서 발썡 -> 함수 +1
  • index 1에서 b 발생 -> 함수 b 1로 업데이트
  • 그다음 a (index 2)-> 함수 a 2로 업데이트
  • 그다음 c (index 3) -> 함수 c 3으로 업데이트
  • 그다음 a (index 4) -> 함수 a 4로 업데이트
  • b (index 5) -> 함수 b 5로 업데이트

Last-occurrence function : O(m+s) time 에 수행가능(P사이즈: m, 시그마사이즈: s)

The Boyer-Moore Algorithm

Algorithm BoyerMooreMatch(T, P, Σ)
    L <- lastOccurenceFunction(P, Σ) // O(m+s) time
    i <- m - 1 // 패턴의 가장 오른쪽 인덱스로 초기화, T의 인덱스
    j <- m - 1 // P의 인덱스
    repeat
    //match 한경우
        if T[i] = P[j]
            if j = 0
                return i { match at i }
            else
                i <- i - 1
                j <- j - 1
    //mismatch한 경우
        else
            { character-jump }
            l <- L[T[i]]
            i <- i + m – min(j, 1 +l) // 두가지 케이스 포함한 수식 : j=case 1, 1+l=case 2
            j <- m - 1 // lookiing-glass 사용하기 위해 항상 P마지막 위치로 업데이트
    until i > n - 1
    return -1 { no match }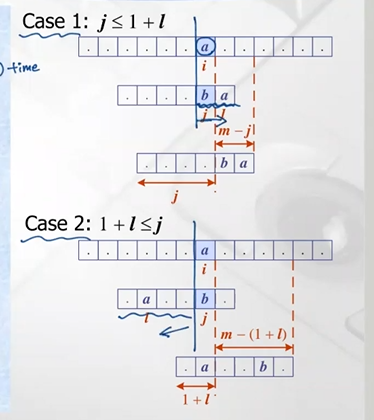

mismatch 발생한 경우 두가지 케이스로 구분가능

  • case 1: bad-character가 같거나 오른쪽에서 발생한경우 -> 단순하게 패턴 오른쪽으로 한칸만 이동
  • case 2: bad-character가 더 왼쪽에서 발생한경우

주의 해야할 점: 패턴을 이동한다는것은 실제로는 text의 인덱스 i를 증가 시켜줘야함
위 예시에서 i를 어떻게 증가시키는가?

  • case 1: m=패턴 길이=6, j=4, 6-4=2 -> i값 2만큼 증가시켜준다
  • case 2: m=6, l=1, 6-(1+1)=4 -> i값 4만큼 증가시켜준다

example

  • 처음부터 mismatch a,b
  • a가 패턴에서 상대적으로 왼쪽에 발생 (항상 마지막 위치만 고려해주자)
  • 패턴을 a에 align 되도록 이동
  • b -> a 일치하다가 (a,c) mismatch
  • 패턴에 a가 bad-char보다 더 오른쪽에 위치
  • 단순히 한칸 이동
  • 처음 a, b mismatch, a가 발생하는 마지막위치 상대적으로 왼쪽
  • a align 되도록 패턴 이동
  • d, b mismatch
  • d 존재 x-> last-occurrence func에 의해 d=-1이므로 패턴이 d이후 align 되도록 이동
  • a,b mismatch
  • a 상대적으로 왼쪽 위치, a align되도록 패턴 이동
  • 패턴 발생, 종료 (13번의 비교)

KMP 알고리즘에 비해 더 빠르게 수행가능

Analysis

Boyer-Moore 알고리즘 수행시간 : O(nm+s)

  • worst case

    • T=aaa..aa

    • P=baaa (항상 매치하다가 마지막에 미스매치 발생하는 경우)

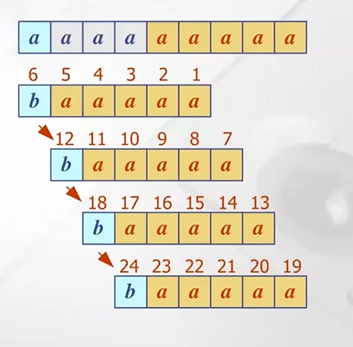      이런경우 계속 브루트 포스 알고리즘과 똑같이 수행 -> O(nm) time 에 수행
  • preprocessing: O(m+s) time
  • searching: O(nm) time
  • total -> O(nm+s) time

worst case의 경우 english text의 경우 거의 발생 x
따라서 Boyer-Moore 알고리즘은 worst case에 대한 수행시간은 느리지만, average case에서는 상당히 빠른 수행시간을 가짐

profile
glow.soon
블로그 이관 했습니다! https://kwonsoonyong-dev.vercel.app/
이전 포스트

9. 다이나믹 프로그래밍

다음 포스트

11. NP-Complete problems

0개의 댓글