지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다

Merge sort

• Problem
  • 오름차순 정렬된 시퀀스 A,B -> 하나의 정렬 시퀀스 C로 merge하기
• Strategy
  • A, B 첫번쨰 원소 비교해서 작은 값 C 맨앞으로 이동시켜 주기 , 점점 작은거 앞으로 채워주면 정렬된 merge 시퀀스 C 얻을수 있다

Merge(A, B, C)
    if (A is empty)
        rest of C = rest of B //A가 빈경우 B 나머지 C에 채우기
    else if (B is empty)
        rest of C = rest of A //B가 빈경우
    else if (first of A ≤ first of B)
        first of C = first of A
        Merge (rest of A, B, rest of C)
    else
        first of C = first of B
        Merge (A, rest of B, rest of C)
    return

최악의 경우 : 빈경우 나머지 채워주는 부분 발생되지 않고, 원소간의 비교연산 많이 하는경우 (A,B 앞부분 번갈아가면서 C에 채워지는 경우)

W(n) = n-1 -> θ(n) time 에 수행

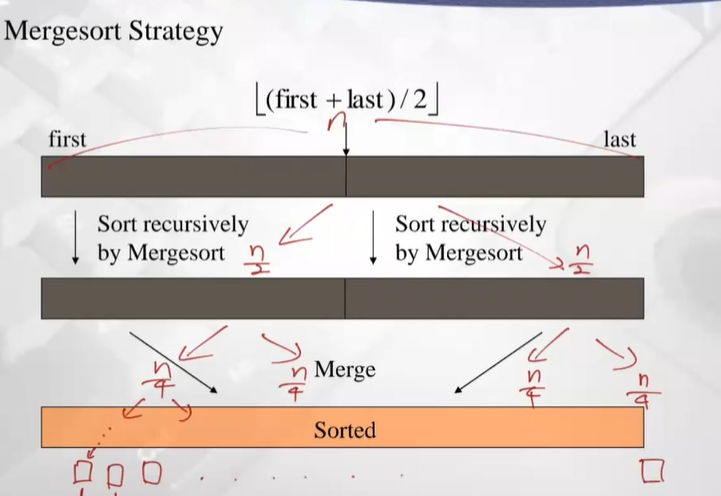
• 위와 같이 계속 재귀적으로 leaf사이즈 1이 될때까지 나눠줌

• 사이즈 1인 원소끼리 비교해서 정렬 merge

ex) [6][5] [3][1] [8][7] [2][4] ->
[5, 6][1, 3] [7, 8][2, 4] ->
[1, 3, 5, 6][2, 4, 7, 8]
-> merge [1, 2, 3, 4, 5, 6, 7, 8]

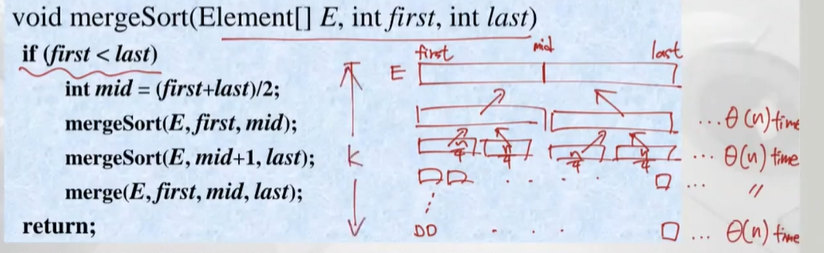
merge 알고리즘과 각각의 level 수행하는데 각각 θ(n) 타임이 걸림, 이것의 height k를 구해보자

마찬가지로 n x (1/2)^k =1, n= 2^k 이라 할수 있으므로 k=logn

그러므로 총 수행시간 W(n/2)+W(n/2)+Wmerge(n) -> θ(nlogn)

• Wmerge(n)=n-1
• W(1)=0

Heap and Heapsort

heap 기본적으로 세가지 기능 지원(maxheap 기준)
1. insert()
2. findMax()
3. deleteMax()

heap은 구조 조건과 순서조건 만족시켜줘야 함

• 구조조건

1. binary tree T는 depth h-1까지는 꽉 차있어야함
2. 모든 leaf노드의 depth는 h or h-1
3. leaf노드 왼쪽부터 채워진다, 삭제는 오른쪽부터 삭제

(이런트리 left-complete binary tree라고도 부름)

• 순서조건
  • 임의의 노드의 키값이 자식노드보다 크거나 같다 (parent(v).key >= v.key)

heapsort Strategy

원소들이 힙으로 잘 정렬되었다면, maxheap이기 때문에 root노드 삭제하면서 가장 뒤에다가 추가

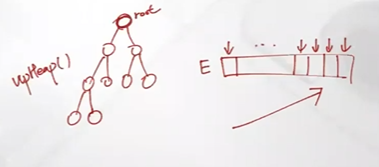(순서 조건 만족시키기 위해 upheap() 함수 사용)

• insert() : O(logn) time
• deleteMax() : root부터 leaf까지 내려갈수 있으므로 O(logn) time
• findMax() : O(1) time (그냥 root노드 찾기)

heapSort(E, n) // Outline
construct H from E, the set of n elements to be sorted // 힙 생성 먼저하기 (O(n) time에 수행)
for (i = n; i ≥ 1; i--)
    curMax = getMax(H)
    deleteMax(H);
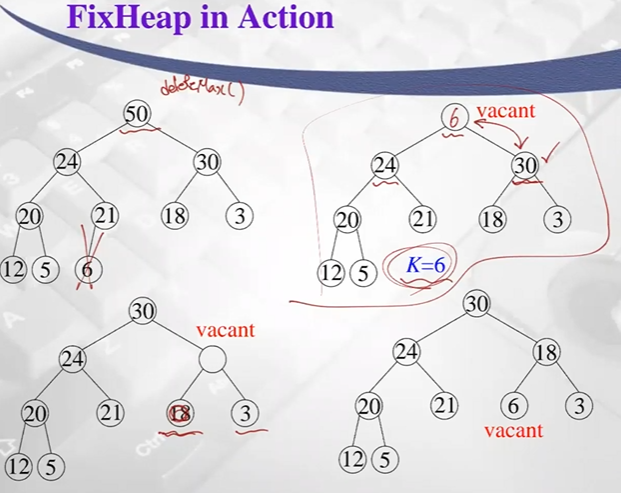
    E[i] = curMax;

deleteMax(X)

가장 아래 level 오른쪽에 있는 key값을 임시변수 K에 카피하고 삭제-> fixHeap 수행 = downHeap

fixHeap(H, K) // Outline
if (H is a leaf)
    insert K in root(H);
else
    set largerSubHeap to leftSubtree(H) or rightSubtree(H), whichever
    has larger key at its root. This involves one key comparison. // 두 자식들 대소비교 (1회비교 연산)
    if (K.key ≥ root(largerSubHeap.key) // key값과 자식노드 중에 큰 자식과 대소 비교 (1회 비교연산) -> 총 2회 비교연산
        insert K in root(H);
    else //만약 자식이 더 크다 ? -> swap시켜줌
        insert root(largerSubHeap) in root(H);
        fixHeap(largerSubHeap, K);
return;

높이를 h라하면 최대 2h의 비교연산 -> W(n)=2log(n)에 bound

Construct Heap Outline (O(n) time)

• input : complete binary tree의 구조는 만족하지만 순서조건은 만족하지 않는 H
• Output : 순서조건까지 만족하는 H

void constructHeap(H) // Outline
if (H is not a leaf)
    constructHeap (left subtree of H); 
    constructHeap (right subtree of H);
    Element K = root(H);
    fixHeap(H, K);
return;

왼쪽 서브트리와 오른쪽 서브트리 힙 만족시킨후 원소하나 root에 추가하고 fixHeap해주기

---

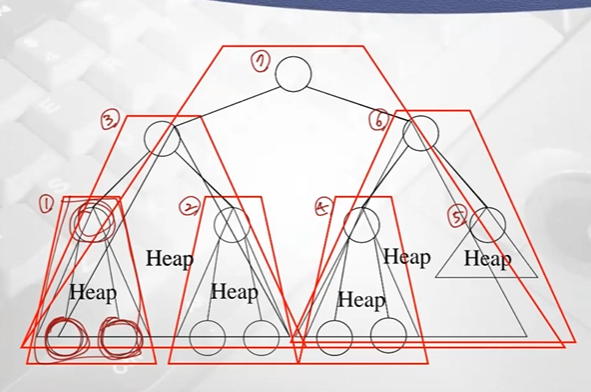
Heap implementation using and Array

• 인덱스 1부터 사용
• 나의 index i일때
  • left child index -> 2i
  • right child index -> 2i+1
  • parent -> i//2

heapsort Analysis

n번의 deleteMax(), fixHeap은 n-1개의 노드에서 수행

-> 2log(n-1)+2log(n-2)+....+2log1 = 2log{(n-1) (n-2) ...*1}=2log(n-1)!

• stitrling's approximation에 의해 log(n!)=>θ(nlogn) -> 2log(n-1)!은 θ(nlogn)에 bound

• heapsort에서 비교연산의 총수는 2nlog(n)=fixheap + O(n) = heap construct => θ(nlogn)에 bound

  • merge, heap sort 모두 optimal

Accelerated heapsort

• 앞선 heapsort보다 2배의 속도 개선 (h comparisons)
• 분할 정복법 적용 (binary search와 비슷)
  1. 서브 heap의 높이 h라했을떄 h/2 까지 내려감
  2. 나의 값 K와 parent 값과 비교
  3. K가 더크면 위쪽 살펴보기 (아래쪽 볼 필요 x)
  4. parent가 더 크면, 재귀적으로 또 h/2 수행(아래로)

void bubbleUpHeap (Element[] E, int root, Element K, int vacant)
if (vacant == root)
    E[vacant] = K;
else // p가 크면 더이상 올라갈 필요 x
    int parent = vacant / 2;
    if (K.key ≤ E[parent].key)
        E[vacant] = K;
    else
        E[vacant] = E[parent]; //k가 p보다 크면 재귀적으로 계속 p와 swap하기
        bubbleUpHeap (E, root, K, parent);

void fixHeapFast(Element[] E, int n, Element K, int vacant, int h)
if (h ≤ 1)
    Process heap of height 0 or 1
else
    int hStop = h/2 // h/2까지 promote함수 통해 내려가기
    int vacStop = promote (E, hStop, vacant, h);
    // vacStop is new vacant location, at height hStop
    int vacParent = vacStop / 2;
    if (E[vacParent].key ≤ K.key) //P값과 나의 값 비교 (내가 더 크면 bubbleupheap 수행)
        E[vacStop] = E[vacParent];
        bubbleUpHeap (E, vacant, K, vacParent);
    else // 내가 작으면 제대로 내려온것, 재귀적 fixheapfast수행
        fixHeapFast (E, n, K, vacStop, hStop);

int promote (Element[] E, int hStop, int vacant, int h)
int vacStop;
if (h ≤ hStop)
    vacStop = vacant;
else if (E[2*vacant].key ≤ E[2*vacant+1].key) // 왼쪽자식 오른쪽 자식 비교해서 큰쪽으로 내려가기
    E[vacant] = E[2*vacant+1];
    vacStop = promote (E, hStop, 2*vacant+1, h-1)
else //왼쪽 자식이 큰 경우
    E[vacant] = E[2*vacant];
    vacStop = promote (E, hStop, 2*vacant, h-1);
return vacStop;

ex)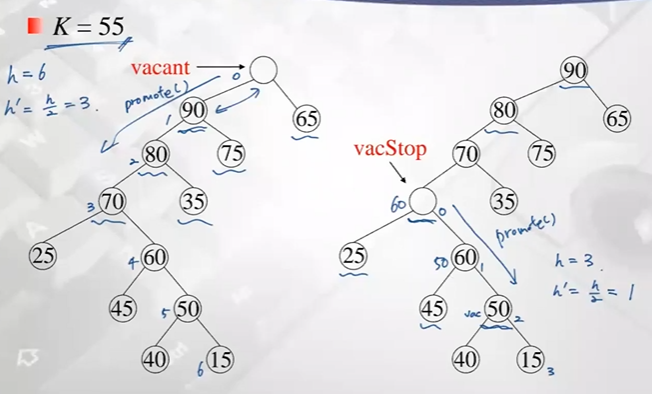

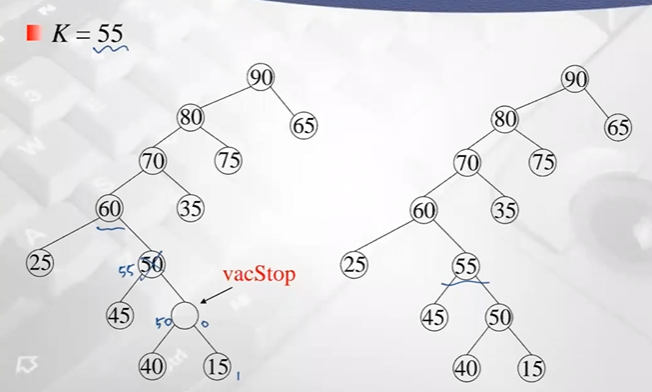
Analysis : fixHeapFast

promote, bubbleUpHeap 함수가 알고리즘 수행시간에 많은 영향 끼친다

• promote나 bubbleUpHeap 한번의 비교연산은 수행해야함

• promote에 의해 h/2만큼 내려간다 가정

  1. 만약 bubbleUpHeap 조건에 걸려 올라간다면 ? 최악의 경우 내려온만큼 다시 올라갈수 있음
     h/2+h/2 -> h
  2. 만약 다시 내려가고, bubbleUpHeap 수행하면
     h/2+h/4+h/4 -> h
  3. h/2+h/4+h/8+h/8 (promote에 의해 계속 내려가고, 마지막에 올라간 경우) -> 이것도 total h

• promote로 계속 내려간 경우는?

  height 1까지 내려갈것임 (worst case)

  h/2+h/4+h/8+.....+1 -> h x (1/2)^k

  (위로갈지 아래로갈지 check 비교 연산수 -> k=logh)

  따라서 w1 = h+log(h)

  (이 때 h는 logn에 bound되므로) w1 = logn+loglogn 이 된다

  Wn = n(logn+loglogn) -> fixHeapFast의 total 수행시간, 따라서 Accelerated Heapsort의 worst case는 nlog(n)+θ(nloglog(n))

  (이론적으로 orginal heapsort 2nlog(n)이었는데 약 2배정도 빨라짐)

Radix Sort

정렬 O(n)에 수행가능한 알고리즘, 알고리즘의 basic operation 다르기에 가능

지금까지는 input 데이터에 대해 선형으로 정렬시킬수 있다고 가정했고, 기본연산은 두개의 키값에 비교연산이었음
만약 key값에 어떤 가정을 더 추가하면, 다른 basic oper 더 고려 가능하다

using properties of the keys

• 키값이 이름일때 //이름의 첫 알파벳에 따라 분류
• 다섯자리의 십진수
• key값들이 제한된 범위로 구성 되었을때 [1, m] -> [1,m/k], [m/k+1, 2m/k], ..... [m/k*(k-1)+1, m]

---

• 각각의 다른 파일(bucket)들로 분류해주고
• 각 파일을 독립적으로 정렬
• 모든 정렬된 파일 combine (기본적으로 분할정복법 idea사용)

키값 구조적, 범위 제한이 있으면 linear time에 수행가능

• Radix sort의 놀라운점 : 각 바구니에 분배할때 아래자리부터 우선 정렬하면 sort과정 생략 가능하다

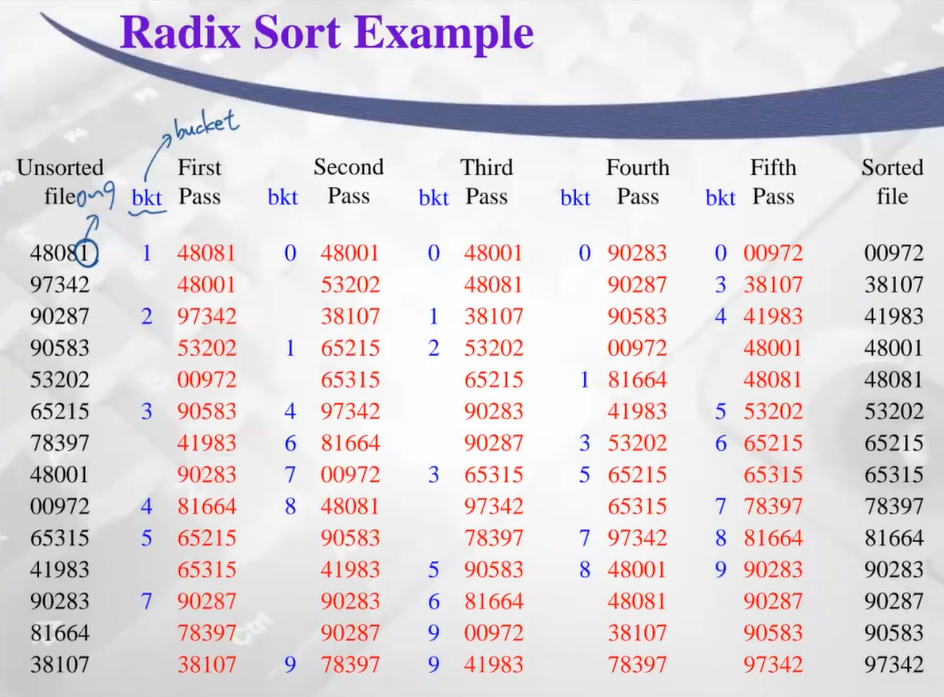
bucket 10개 만들어주기

pass1: 1의자리 1이다 -> 버킷 1에 채우기 ..... ->
pass2: 10의 자리 숫자에 따라 분배, 순서유지되도록 combine ..... -> pass 5 까지 수행

• loop invairant로 증명가능

1. 첫번쨰 pass잘 수행해주면 첫번째 자리수에 대해 오름차순으로 잘 정렬됨
2. i번째 step : i번째 pass 시작하기 전에 i-1 자리까지는 오름차순으로 잘 정렬되어있다 , i번째 수행하면 i번째 자리까지는 오름차순으로 잘 정렬되어있음
3. termianation step : 마지막까지 잘 수행해주면 오름차순으로 정렬 잘 되어있음

stable sort란

a1,a2,a3 인 순서를 가지는 원소가 있고 각각 값이 다 같다고 할때 정렬을 수행한 경우 상대적인 순서 그대로 유지할 때 -> stable 하다

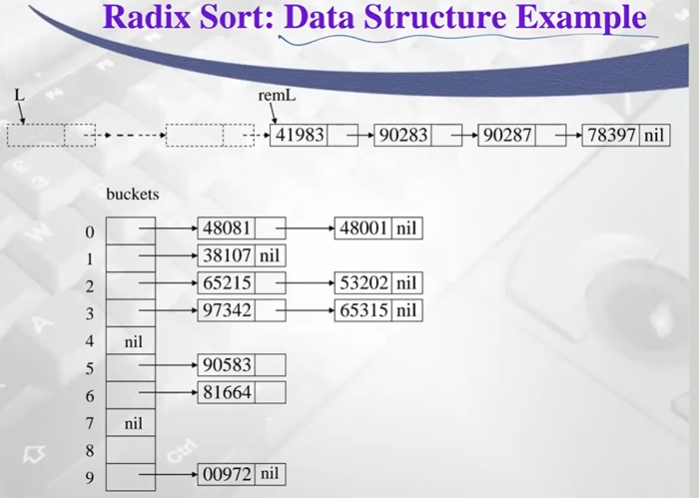
(ex. pass 3 수행하는중)

41983, 90283, 90287, 78397만 남은 상황

bucket에 삽입할때 해당 index list head에 삽입

분배 단계에서 하나의 원소 distribute할때 상수시간에 처리가능, n개의 원소 처리해줘야 하므로

• distribution : θ(n) time
• combine : 하나의 원소 삭제할때 head에서 삭제, 삽입 연산 : O(n) time -> 추가적으로 각 bucket k개의 index에 접근해야 하므로 총 θ(k+n) time

• i th pass : θ(k+n) time
• 자리수가 d개 있다고 가정하면, pass 역시 d번의 pass수행해야함, Total : θ(d(k+n)) time (when k, d가 상수이면 θ(n) time 에 수행가능)

Radix Sort : analysis

• distribute : θ(n)
• combine : θ(k+n)
• 시간 복잡도 : θ(d(k+n)) time
• 공간 복잡도 : θ(k+n) space