지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다

Dynamic Sets and Searching

시간흐름에 따라 크기 달라지는 자료구조

• Amortized Analysis - Array doubling
• BST - Red Black Tree

Array doubling

어떤 계산 시작할때 필요한 array사이즈 알기 힘듬

• 새로운 원소를 넣을때 더이상 공간이 없으면?

  • 현재 array보다 2n배 array 할당해준다
  • 기존 원소들 새로운 array로 이동(copy)

• t을 원소하나 이동하는데 필요한 비용이라 하자

이런 형태를 가질것이다

• n+1의 원소를 array doubling 해야한다 가정
• array doubling 연산에 tn의 비용이 들것
• 그 전 과정의 비용도 따져보자 => t x n + t x n/4 + t x n/8 ... + t x 1

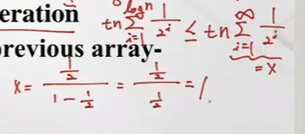위와같은 식으로 정리가능 => tn보다 클 수 없다

• 총 t x n + t x n = 2t x n의 cost 필요

insertion operation에 대한 worst case : O(tn) time (t를 상수라 하면) => O(n) time

원래 삽입하는데 상수시간에 처리 되지만 array doubling 때문에 O(n)의 최악수행시간이 나와 불합리한 느낌이듬

교수님이 설명한 실생활에서의 사례 : 하루에 식비 만원씩 쓰는 회사원, 매달 말일에는 고생한 나에게 주는 보상으로 식비 10만원씀, 이것을 worst case로 분석해보면 하루에 식비를 10만원 쓰는 꼴이됨, 틀린말은 아니지만 억울, 이런경우 쓸수 있는 분석 방법 => Amortized analysis

Amortized analysis

worst case 분석의 일종, 최악의 경우 각 연산의 비용의 평균이 몇인가?

1. aggregate method - 비용들 평균내는 방식
2. accounting method - 분할상환방법 (이거 다룰것임)
3. potential method

ex ) 매일 만원의 식비를 쓰지만, 말일을 위해 매일 4천원씩 저축 -> 실제 사용 비용 만원 : actual cost, 저축 비용 : accounting cost

accounting cost + actual cost = amortized cost

• 목돈 커버하려면 평상시 얼마를 저축해놔야 할까?
  • 상황에따라 다른 accounting cost 할당해주기
  1. accounting cost 차감될때마다 계좌의 남은 잔액 음수가 되면 안됨
  2. amortized cost 분석에 용이하게끔 설정하기

implementing stack with Array doubling

2t를 계속 계좌에 넣어야 0이상을 유지 할 수있음 (그냥 외우자...)

• doubling 발생 하지 않을때 push or pop하는 actual cost = 1

• doubling 발생 할 때 actual cost = 1+t*n

• doubling 발생 x일때 accounting cost = 2t

• doubling 발생 했을때 accounting cost = transferring cost 차감 해주기 = -t*n+2t

즉, doubling 안일어난 경우 비용 = 1+2t, doubling 발생한경우 일어난 비용 = (1+tn) + (-tn+2t) = 1+2t

push연산 계속 일어난 경우의 amortized cost = 1+2t => amortized O(t) time

(만약 t가 constant이면) => amortized O(1) time

• worst case analysis
  -가장 기본적인 분석방법, 거의 무조건 분석함
• average case analysis (optional)
  -확률의 개념이 존재
• amortized analysis (optional)
  -일단 worst case에 대한 분석, 비용의 평균, 특정 case에서 갑자기 많은 비용들때 분석하는것이 좋음