Baek_10799_Stack
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;
public class Baek_10799_Stack {
public static void main(String[] args) throws IOException {
// (를 만나면 stack에 넣기
// )를 만나면 stack의 바로 위에 데이터가 (인지 판단해서 (이면 레이저,
// 그렇지 않으면 막대기의끝(끝이면 잘렸을때 하나 남으니까 한개 더하기
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String line = br.readLine();
System.out.println(count(line));
}
public static int count(String str) {
int result = 0; //잘리는 쇠막대기의 갯수를 저장할 변수
Stack<Character> stack = new Stack<>();
int size = str.length();
for(int i=0;i<size;i++) {
//System.out.println(str.charAt(i));
if(str.charAt(i)=='(') {//여는괄호
stack.push('(');
}else {//닫는괄호
stack.pop();
if(str.charAt(i-1)=='(') {//레이저 - 바로직전 문자열
//스택에 저장된 (괄호가 막대기의 시작점
result = result + stack.size();
}else {
//쇠막대기 끝
result = result + 1;
}
}
}
return result;
}
}search
SequenceSearchTest
95페이지 검색알고리즘
98페이지 선형검색
두번째과제 - 선형검색
import java.util.Scanner;
public class SequenceSearchTest {
public static void main(String[] args) {
Scanner key = new Scanner(System.in);
int[] arr = {77,19,22,23,7,4,5};
System.out.print("찾을숫자: ");
int searchValue = key.nextInt();
long start = System.nanoTime();
int result = search(arr, searchValue);
long end = System.nanoTime();
System.out.println("걸린시간:"+(end-start));
//찾는 숫자는 배열에서 6번 위치에 있습니다
//찾는 숫자는 배열에 없습니다
if(result!=-1) {
System.out.println("찾는 숫자는 배열에서 "+(result+1)+"번 위치에 있습니다.");
}else {
System.out.println("찾는 숫자는 배열에 없습니다.");
}
}
//searchValue의 위치를 리턴, 없으면 -1을 리턴하기
//arr가 찾으려고 하는 값이 저장된 배열
//searchValue가 실제 찾는 값
public static int search(int[] arr, int searchValue) {
int result = 0;
for(int i=0;i<arr.length;i++) {
if(arr[i]==searchValue) {
result = i;
}else {
result = -1;
}
}
return result;
}
}SequenceSearch_SentinelTest
보초법
- 효율성을 높이기 위해서 사용되는 방법
- 순차검색에서 각 요소에 조건을 적용해서 비교하면서 조건을 만족하지 않는 경우에 대한 처리를 진행하므로 이부분에 대한 연산을 최소화하자는 의미
- 보초법은 배열의 마지막에 찾으려고 하는 값을 추가해서 검색 - 추가조건 검색이 필요
보초법(Sentinel)의 역할
보초법에서 중요한 부분은 배열의 마지막 요소로 찾고자 하는 값을 미리 넣어 두는 것입니다. 이를 통해 검색 루프 내에서 항상 값이 발견되도록 보장합니다. searchValue가 배열의 마지막 위치에 있으므로, 만약 찾고자 하는 값이 배열 내에 없다면, 보초값이 있는 위치가 반환됩니다.
다시 말해, 이 코드는 배열의 모든 요소를 확인하며, 마지막에 있는 보초값에 도달할 때까지 값을 찾지 못했다면, result가 배열의 마지막 인덱스(arr.length - 1)가 됩니다. 이는 if (result == arr.length - 1) 조건을 통해 값이 배열에 없다는 것을 확인하게 합니다.
이 방식은 불필요한 비교를 줄여 검색 과정을 단순화하고, 코드의 성능을 약간 향상시킬 수 있습니다.
public class SequenceSearch_SentinelTest {
public static void main(String[] args) {
Scanner key = new Scanner(System.in);
System.out.print("찾을숫자: ");
int searchValue = key.nextInt();
int[] arr = {77,19,22,23,7,4,5,searchValue};
//System.out.println("===size"+arr.length);
long start = System.nanoTime();
int result = search(arr, searchValue);
long end = System.nanoTime();
System.out.println("걸린시간:"+(end-start));
//찾는 숫자는 배열에서 6번 위치에 있습니다
//찾는 숫자는 배열에 없습니다
if(result==arr.length-1) {
// 검색 결과 result가 배열의 마지막 인덱스(arr.length - 1)와 같다면, 찾는 값이 배열에 없음을 의미합니다. 그렇지 않다면, 찾는 값의 위치를 출력합니다.
System.out.println("찾는 데이터가 없습니다.");
}else {
System.out.println("데이터의 위치:"+result);
}
}
//searchValue의 위치를 리턴, 없으면 -1을 리턴하기
//arr가 찾으려고 하는 값이 저장된 배열
//searchValue가 실제 찾는 값
public static int search(int[] arr, int searchValue) {
int result = 0;
for(int i=0;i<arr.length;i++) {
if(arr[i]==searchValue) {
result = i;
break;
}
}
return result;
}
}BinarySearchTest
- 정렬해서 보기

106페이지 이진검색
115
import java.util.Arrays;
import java.util.Scanner;
//이진탐색의 조건은 정렬이 기본으로 되어있는 상태
public class BinarySearchTest {
public static void main(String[] args) {
Scanner key = new Scanner(System.in);
System.out.print("찾을숫자: ");
int searchValue = key.nextInt();
int[] arr = {77,19,22,23,7,4,5,33};
Arrays.sort(arr);//원본이 변경되어 정렬
System.out.println(Arrays.toString(arr));
int result = search(arr, searchValue);
if(result==-1) {
System.out.println("찾는 데이터가 없습니다.");
}else {
System.out.println("데이터의 위치:"+result);
}
}
public static int search(int[] arr,int searchValue) {
int searchIndex = -1;
//시작 index, 종료 index, 중앙 index
//찾는 위치는 원본에서 보이는 위치가 아니라 정렬된 배열에서의 위치
//1. 전체배열에서 중앙값을 찾는다.
//2. 중앙값과 찾는값을 비교
//3. 중앙값>찾는값일때 중앙값을 기준으로 왼쪽의 데이터들만 비교
//4. 중앙값<찾는값일때 중앙값을 기준으로 오른쪽의 데이터들만 비교
//5. 1~4번까지를 값을 찾을때까지 반복(index를 변경)
int startIndex = 0;
int endIndex = arr.length-1;
//중앙값
int mediumIndex = 0;
while(startIndex<=endIndex) {
mediumIndex = (startIndex+endIndex)/2;
System.out.println(startIndex+","+mediumIndex+","+endIndex);
//중앙값과 찾으려고 하는 값을 비교 - >, <, ==
if(arr[mediumIndex]==searchValue) {
searchIndex = mediumIndex;
break;
}else if(arr[mediumIndex]>searchValue) {
//찾으려는 값보다 중앙값이 더 크면 중앙값 뒤의 값들은 처리하지않는다.
endIndex = mediumIndex-1;
}else {
//찾으려는 값보다 중앙값이 더 작으면 중앙값 앞의 값들은 처리하지않는다.
startIndex = mediumIndex+1;
}
}
return searchIndex;
}
}Baek_1920_Search
미션
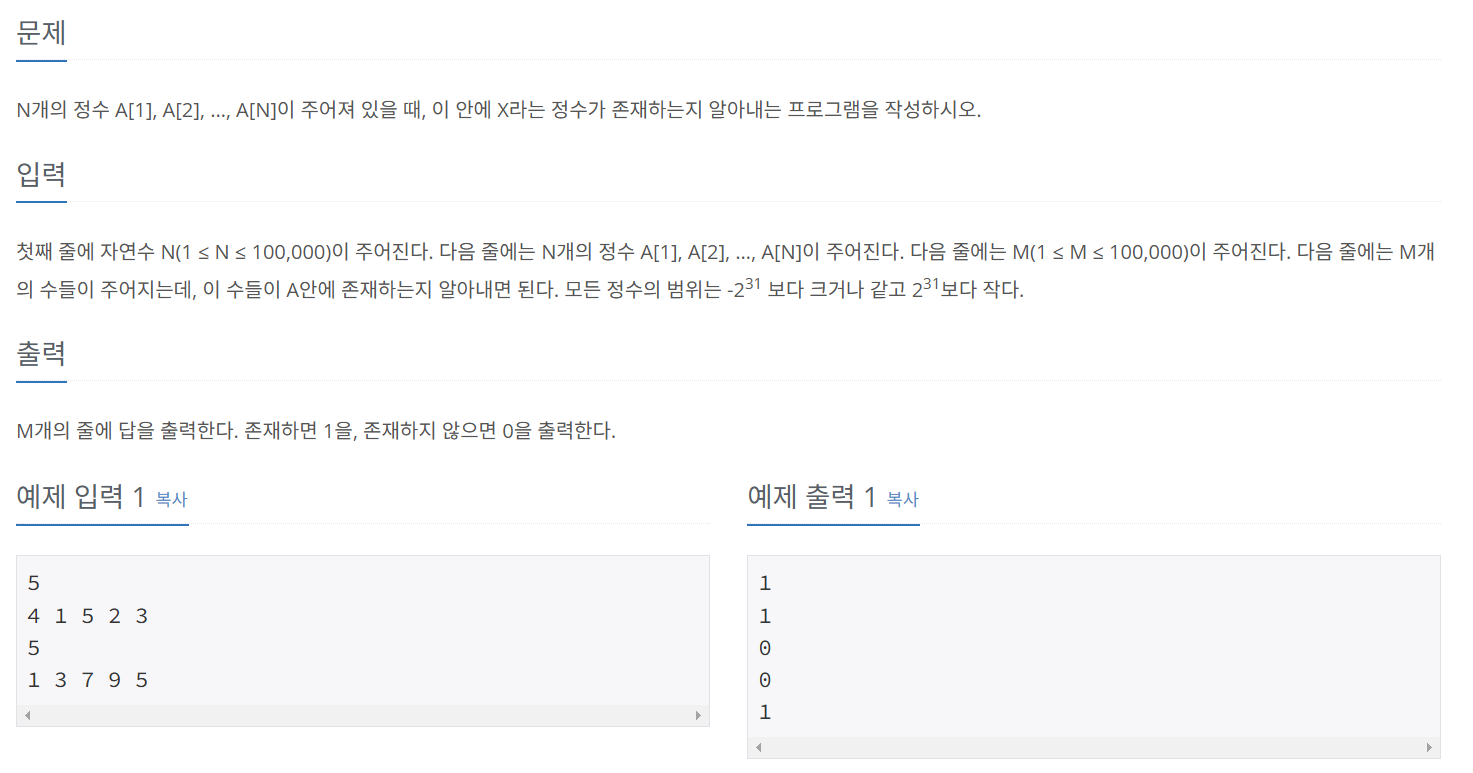
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Baek_1920_Search {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
//1. 검색할 원본배열을 입력받아 만들기
int datasize = Integer.parseInt(br.readLine());
int[] dataarr = new int[datasize];
//n개의 숫자만큼 입력을 받아서 배열에 저장
String dataline = br.readLine();
//spacebar기준으로 분리
String[] stingarr = dataline.split(" ");
for(int i=0;i<datasize;i++) {
dataarr[i] = Integer.parseInt(stingarr[i]);
}
//2. 배열을 정렬하기
Arrays.sort(dataarr);
//3. 찾을 문자열과 갯수를 입력받아서 배열로 변환
int searchSize = Integer.parseInt(br.readLine());
String searchline = br.readLine();
String[] searchValueArr = searchline.split(" ");
//찾을 숫자의 갯수만큼 for문을 반복해서 실행해서 찾을 숫자를 입력받아 해당 배열에 있는지 찾기
for(String searchValue : searchValueArr) {
System.out.println(search(dataarr, Integer.parseInt(searchValue)));
}
}
//값이 있는 경우 1을 반환, 없는 경우 0을 반환
public static int search(int[] arr,int searchValue) {
int searchIndex = 0;
int startIndex = 0;
int endIndex = arr.length-1;
//중앙값
int mediumIndex = 0;
while(startIndex<=endIndex) {
mediumIndex = (startIndex+endIndex)/2;
//System.out.println(startIndex+","+mediumIndex+","+endIndex);
//중앙값과 찾으려고 하는 값을 비교 - >, <, ==
if(arr[mediumIndex]==searchValue) {
searchIndex = 1;
break;
}else if(arr[mediumIndex]>searchValue) {
//찾으려는 값보다 중앙값이 더 크면 중앙값 뒤의 값들은 처리하지않는다.
endIndex = mediumIndex-1;
}else {
//찾으려는 값보다 중앙값이 더 작으면 중앙값 앞의 값들은 처리하지않는다.
startIndex = mediumIndex+1;
}
}
return searchIndex;
}
}sort
SwapTest
import java.util.Arrays;
public class SwapTest {
public static void main(String[] args) {
int[] num = {4,5,2,4,8,9};
System.out.println(Arrays.toString(num));
//5와 8을 교환(swap)
int temp = num[1];
num[1] = num[4];
num[4] = temp;
System.out.println(Arrays.toString(num));
}
}BubbleSortTest
import java.util.Arrays;
/*버블정렬
* ->바로 옆에 있는 값을 비교해서 작은 숫자를 앞으로 큰 숫자를 뒤로 교환
* ->반복
*/
public class BubbleSortTest {
public static void main(String[] args) {
int[] arr = {77,19,22,23,7,4,5};
for(int i=0;i<arr.length-1;i++) {
for(int j=0;j<arr.length-1-i;j++) {
System.out.println("i:"+i+",j:"+j+",arr[j]:"+arr[j]+",arr[j+1]:"+arr[j+1]);
//비교
if(arr[j]>arr[j+1]) {
//swap하기-값이 큰 경우 뒤쪽으로 보내기
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
System.out.println(Arrays.toString(arr));
System.out.println();
}
}
}선택정렬과 퀵정렬의 차이
선택 정렬 (Selection Sort)
- 작동 방식:
리스트를 처음부터 끝까지 쭉 살펴보면서 가장 작은 값을 찾습니다.
그 값을 리스트의 맨 앞자리 값과 교환합니다.
두 번째 자리부터 끝까지 다시 살펴보면서 가장 작은 값을 찾습니다.
그 값을 두 번째 자리 값과 교환합니다.
이 과정을 리스트 끝까지 반복합니다. - 예시:
주어진 리스트: [3, 1, 4, 1, 5]
첫 번째 탐색: 가장 작은 값은 1 → [1, 3, 4, 1, 5]
두 번째 탐색: 두 번째 자리부터 가장 작은 값은 1 → [1, 1, 4, 3, 5]
세 번째 탐색: 세 번째 자리부터 가장 작은 값은 3 → [1, 1, 3, 4, 5] - 특징:
시간 복잡도: O(n^2) (리스트의 크기가 n일 때)
공간 복잡도: O(1) (추가 메모리 사용 거의 없음) - 장점: 구현이 간단하고 직관적
- 단점: 비효율적이며 큰 데이터셋에 비적합
퀵 정렬 (Quick Sort)
- 작동 방식:
리스트에서 하나의 기준점(pivot)을 선택합니다.
이 기준점보다 작은 값들은 왼쪽에, 큰 값들은 오른쪽에 배치합니다.
기준점을 중심으로 리스트를 두 개의 하위 리스트로 분할합니다.
분할된 하위 리스트에 대해 재귀적으로 퀵 정렬을 적용합니다. - 예시:
주어진 리스트: [3, 1, 4, 1, 5]
기준점 선택 (예: 3)
3보다 작은 값들: [1, 1], 큰 값들: [4, 5] → [1, 1, 3, 4, 5][1, 1]과 [4, 5]에 대해 다시 퀵 정렬 적용 (이미 정렬된 상태) - 특징:
시간 복잡도: 평균 O(n log n), 최악의 경우 O(n^2) (리스트가 이미 정렬되어 있는 경우 등)
공간 복잡도: O(log n) (재귀 호출에 의한 메모리 사용) - 장점: 평균적으로 매우 빠르고 효율적
- 단점: 최악의 경우가 존재하고, 재귀 호출로 인해 추가 메모리 사용
비교 요약
- 선택 정렬: 구현이 쉽고 추가 메모리 사용이 거의 없지만, 시간 복잡도가 높아 큰 데이터셋에는 비효율적.
- 퀵 정렬: 평균적으로 매우 빠르고 효율적이지만, 재귀 호출로 인해 추가 메모리를 사용하며 최악의 경우가 존재.
이렇게 선택 정렬과 퀵 정렬은 각각의 장단점이 있으며, 어떤 정렬 방법을 사용할지는 데이터의 크기와 특성에 따라 달라질 수 있습니다.
본 포스팅은 멀티캠퍼스의 멀티잇 백엔드 개발(Java)의 교육을 수강하고 작성되었습니다.
