❗모든 코드의 앞에는 import numpy as np를 썼다고 가정하겠습니다.
글 내용 순서는 '머신러닝을 위한 수학 - 이병준 저'를 참고했습니다.
NumPy?
NumPy는 다차원 배열로 행렬을 표현하며, 수학적 연산을 위한 다양한 함수와 메서드를 제공하여 행렬 계산과 변환을 용이하게 합니다. 이를 통해 데이터 과학, 머신 러닝 등 다양한 분야에서 행렬을 이용한 연산을 효과적으로 수행할 수 있습니다.
행렬 (matrix)
행렬이 머신러닝에서 중요한 이유는 데이터를 다루고 연산하는 데 효율적이기 때문이다. 행렬은 많은 양의 데이터를 표현하고, 여러 가지 수학적인 작업을 쉽게 할 수 있게 도와준다. 예를 들면, 여러 변수 간의 관계를 파악하거나 데이터를 변환하고 모델을 훈련시킬 때 유용하게 사용된다. 이런 작업들을 효율적으로 처리할 수 있게 도와주는 도구로서 행렬은 머신러닝에서 핵심적이다.
행렬
행렬은 숫자나 기호들을 행과 열로 배열한 것.
일반적으로 행렬은 개의 행과 개의 열로 이루어진다.
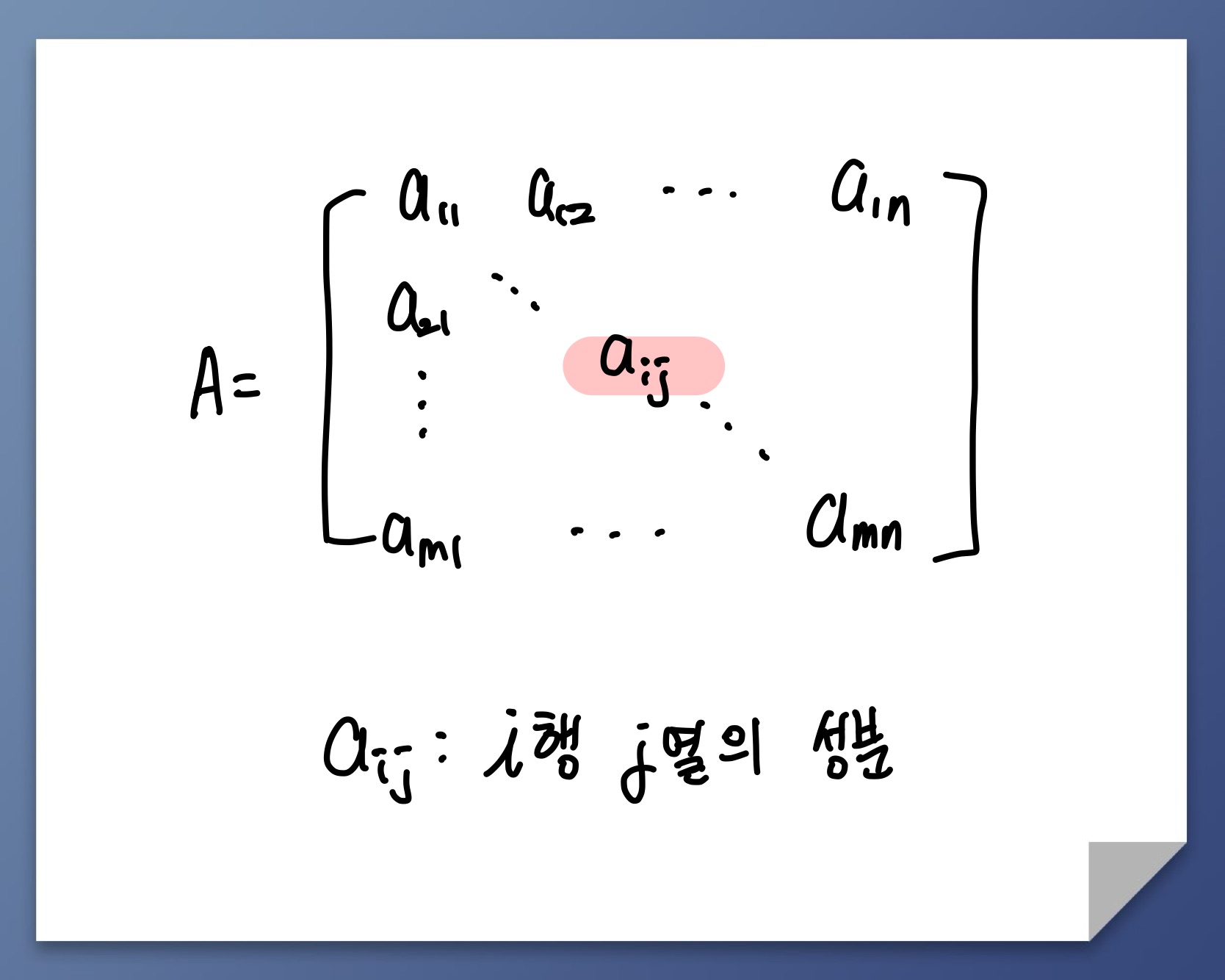
🧑🏻💻 행렬은 np.array([[1행],[2행],...,[n행]])으로 표현이 가능하다.
a=np.array([[1,2,3],[2,4,6]])
print(a)[[1 2 3] [2 4 6]]
정사각행렬
행과 열의 크기가 같은 행렬
a=np.array([[1,2,3],[2,4,6],[3,6,9]])
print(a)[[1 2 3] [2 4 6] [3 6 9]]
영행렬 (zero matrix)
모든 성분이 인 행렬
🧑🏻💻 영행렬은 np.zeros((m,n))으로 영행렬 표현이 가능하다.
zeros=np.zeros((3,4))
print(zeros)[[0. 0. 0. 0.] [0. 0. 0. 0.] [0. 0. 0. 0.]]
행렬의 덧셈과 스칼라곱
같은 크기의 행렬끼리 합은 같은 위치의 성분끼리 더한다
행렬에 스칼라 를 곱하면 모든 성분에 가 곱해진다
a=np.array([[1,2,3],[2,4,6]])
b=np.array([[100,50,10],[100,50,10]])
print('행렬a')
print(a)
print('')
print('행렬b')
print(b)
print('')
print('a+b')
print(a+b)
print('')
print('10*(행렬 a)')
print(10*a)행렬a [[1 2 3] [2 4 6]] 행렬b [[100 50 10] [100 50 10]] a+b [[101 52 13] [102 54 16]] 10*(행렬 a) [[10 20 30] [20 40 60]]
행렬의 덧셈과 스칼라곱 성질
행렬 , 영행렬 와 실수 에 대하여
1.
2.
3.
4.
행렬의 곱
A = np.arange(6).reshape([2,3]) # [0,1,2,3,4,5,6]을 2x3행렬로
B = np.arange(0,12,2).reshape(([3,2])) # [0,2,4,6,8,10,12]를 3x2행렬로
print('A행렬'); print(A,'\n')
print('B행렬'); print(B,'\n')
print('행렬 곱'); print(A@B) #행렬 곱A행렬 [[0 1 2] [3 4 5]] B행렬 [[ 0 2] [ 4 6] [ 8 10]] 행렬 곱 [[20 26] [56 80]]
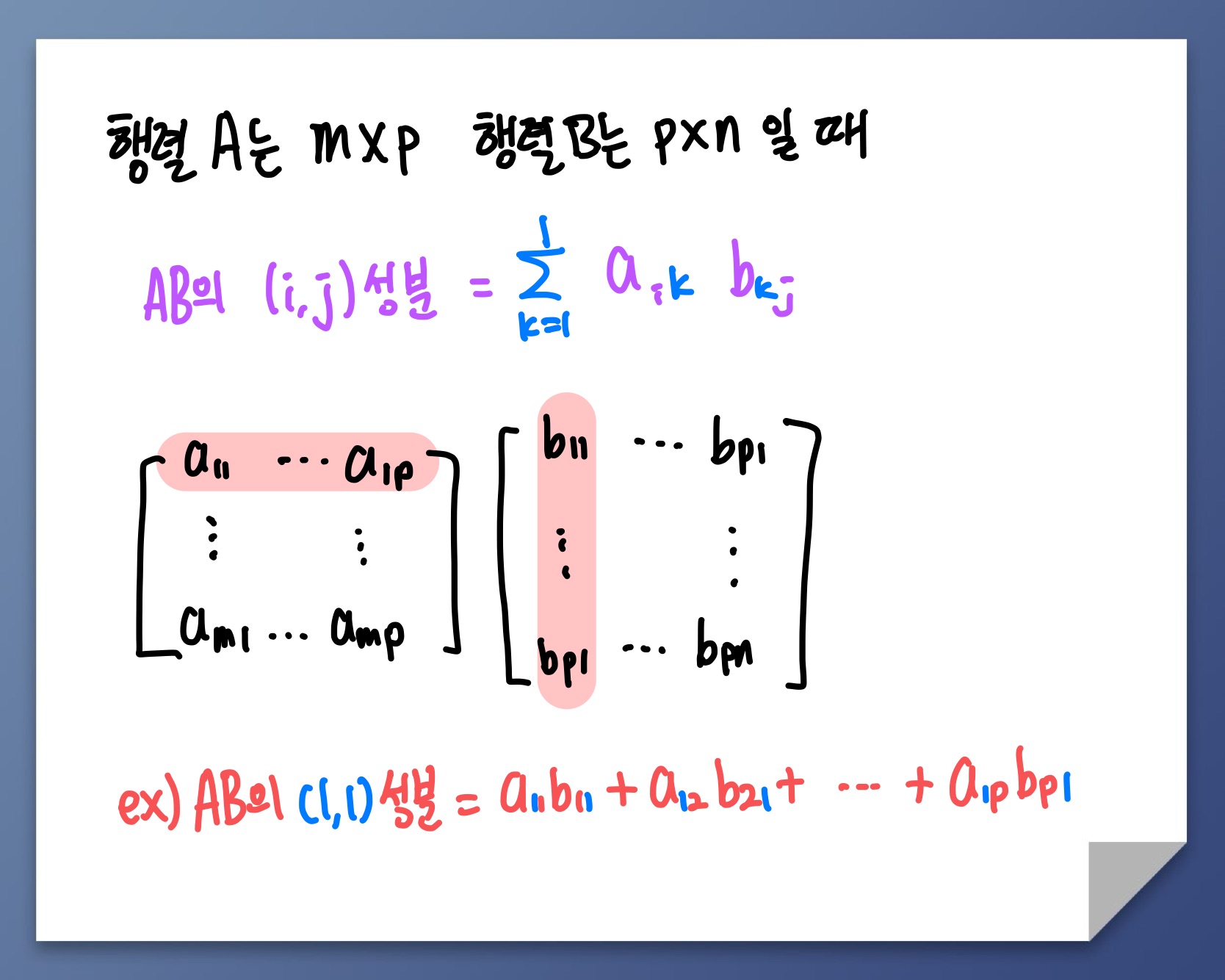
행렬의 곱 성질
행렬 에 대하여
1.
2.
❗ 는 조건에 따라 성립하는 경우가 있긴 하지만 대부분 성립하지 않는다
🔔항등행렬 (identity matrix)
행렬에서 대각성분만 이고 나머지는 인 행렬
🧑🏻💻 항등행렬은 np.identity(n)을 통해 표현이 가능하다.
id = np.identity(4)
print(id)[[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
❗항등행렬은 행렬의 곱에서 항등원 역할을 한다.
전치행렬 (transpose matrix)
행렬 의 행과 열을 뒤바꾼 행렬()
🧑🏻💻 전치행렬은 np.transpose(matrix)를 통해 표현이 가능하다.
A = np.arange(6).reshape([2,3])
trans_A = np.transpose(A)
print('기존 A')
print(A)
print('='*30)
print('A의 전치행렬')
print(trans_A)기존 A [[0 1 2] [3 4 5]] ============================== A의 전치행렬 [[0 3] [1 4] [2 5]]
대칭행렬 (symmetric matrix)
n x n 정사각행렬 와 그 전치행렬 이 동일한 행렬
sym = np.array([[0,2,0],[2,4,2],[0,2,8]])
print(sym)[[0 2 0] [2 4 2] [0 2 8]]
🔔역행렬 (inverse matrix)
n x n 정사각행렬 A, B 와 항등행렬 I가 있을 때
가 성립하면 B는 A의 역행렬()이라 한다.
🧑🏻💻 역행렬은 np.linalg.inv(matrix)를 통해 표현할 수 있다.
matrix = np.array([[1,2,3],[0,1,2],[2,3,0]])
inv_matrix = np.linalg.inv(matrix)
print('기존 행렬');print(matrix)
print('-'*30)
print('역행렬');print(inv_matrix)
print('='*30)
print('기존 행렬과 역행렬의 곱');print(matrix@inv_matrix)
print('-'*30)
print('역행렬과 기존 행렬의 곱');print(inv_matrix@matrix)기존 행렬 [[1 2 3] [0 1 2] [2 3 0]] ------------------------------ 역행렬 [[ 1.5 -2.25 -0.25] [-1. 1.5 0.5 ] [ 0.5 -0.25 -0.25]] ============================== 기존 행렬과 역행렬의 곱 [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]] ------------------------------ 역행렬과 기존 행렬의 곱 [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
❗️ 역행렬은 행렬의 곱에서 역원 역할을 한다.
행렬의 역행렬
의 역함수는 일 때,
이 뒤로는 같은 방식으로 쭉 노가다 하면 나머지 도 구할수 있다!
이때 행렬 의 역행렬에 나온 식 은
행렬식이라 부른다. 혹은 로 표현한다.
🔔행렬식 (determinant)
행렬식은 주어진 정방 행렬이 어떤 선형 변환에 의해 부피(면적 또는 부피)가 어떻게 변하는지를 나타내는 수치다. 간단히 말하면, 행렬식은 변환된 영역의 크기 변화를 설명해준다. 행렬식이 양수인 경우, 변환은 부피를 확대시키거나 원래 모양을 유지한다. 행렬식이 음수인 경우, 변환은 부피를 반전시키거나 방향을 뒤집을 수 있다. 이때, 행렬식이 0이면, 해당 변환은 부피를 압축시키거나 특정 차원을 줄이는 것으로 이해할 수 있다. 행렬의 행렬식이 0이면 역함수를 구할 수 없다.
행렬 에서 행과 열을 없앤 새로운 행렬을 라고 할때
행렬식을 구하는 공식은
이다.
시각적으로 표현해보면
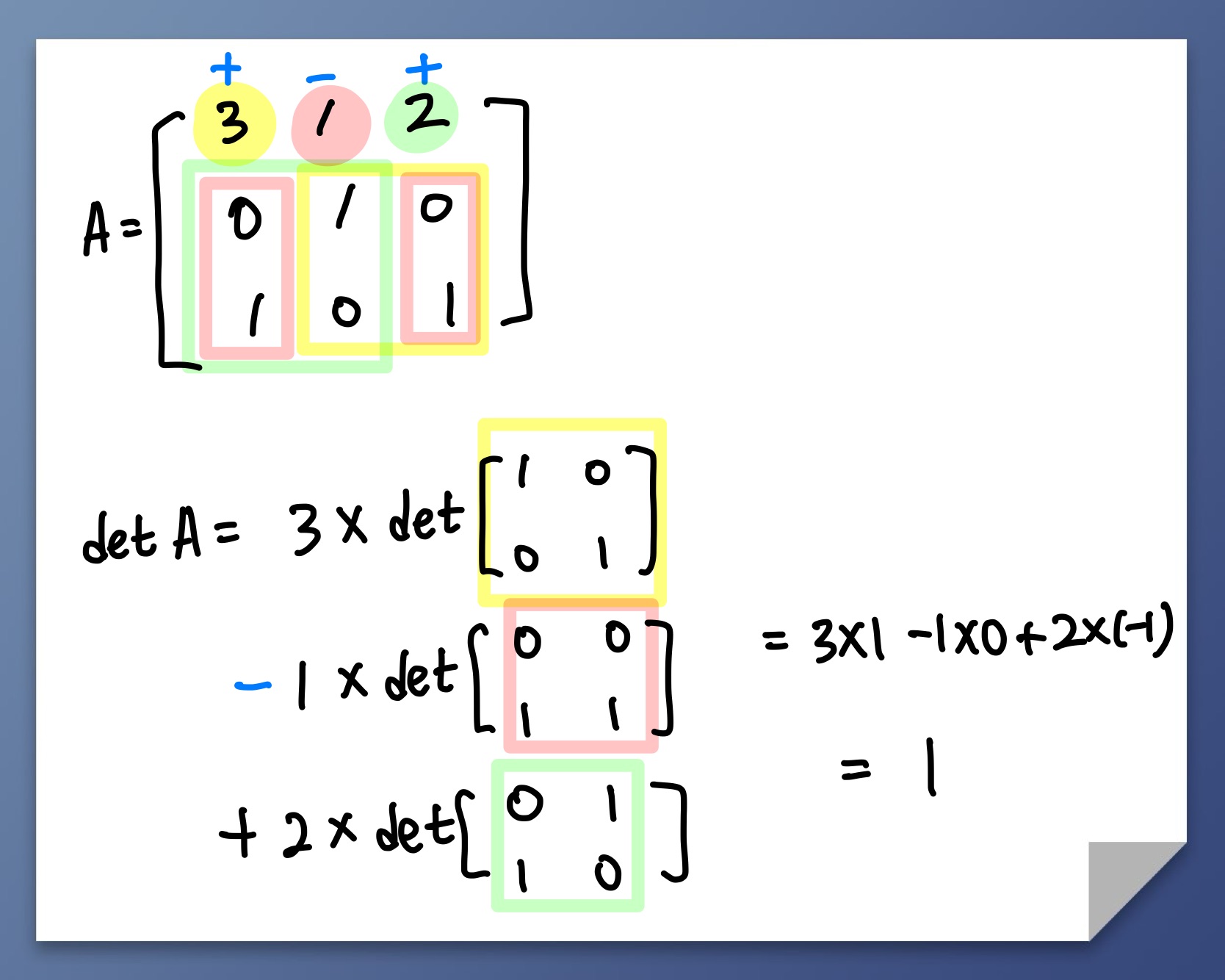
이때
소행렬식 :
여인자 : 라고 할 때
이다.
🧑🏻💻 행렬식은 np.linalg.det(matrix)로 구할 수 있다.
matrix = np.array([[3,1,2],[0,1,0],[1,0,1]])
print(np.linalg.det(matrix))1.0000000000000002
행렬의 역행렬
행렬 의 역함수가 존재할 때
이다.
🧑🏻💻 행렬식, 역행렬 직접 코딩 해보기!
아이디어를 간단하게 도식화 해보면
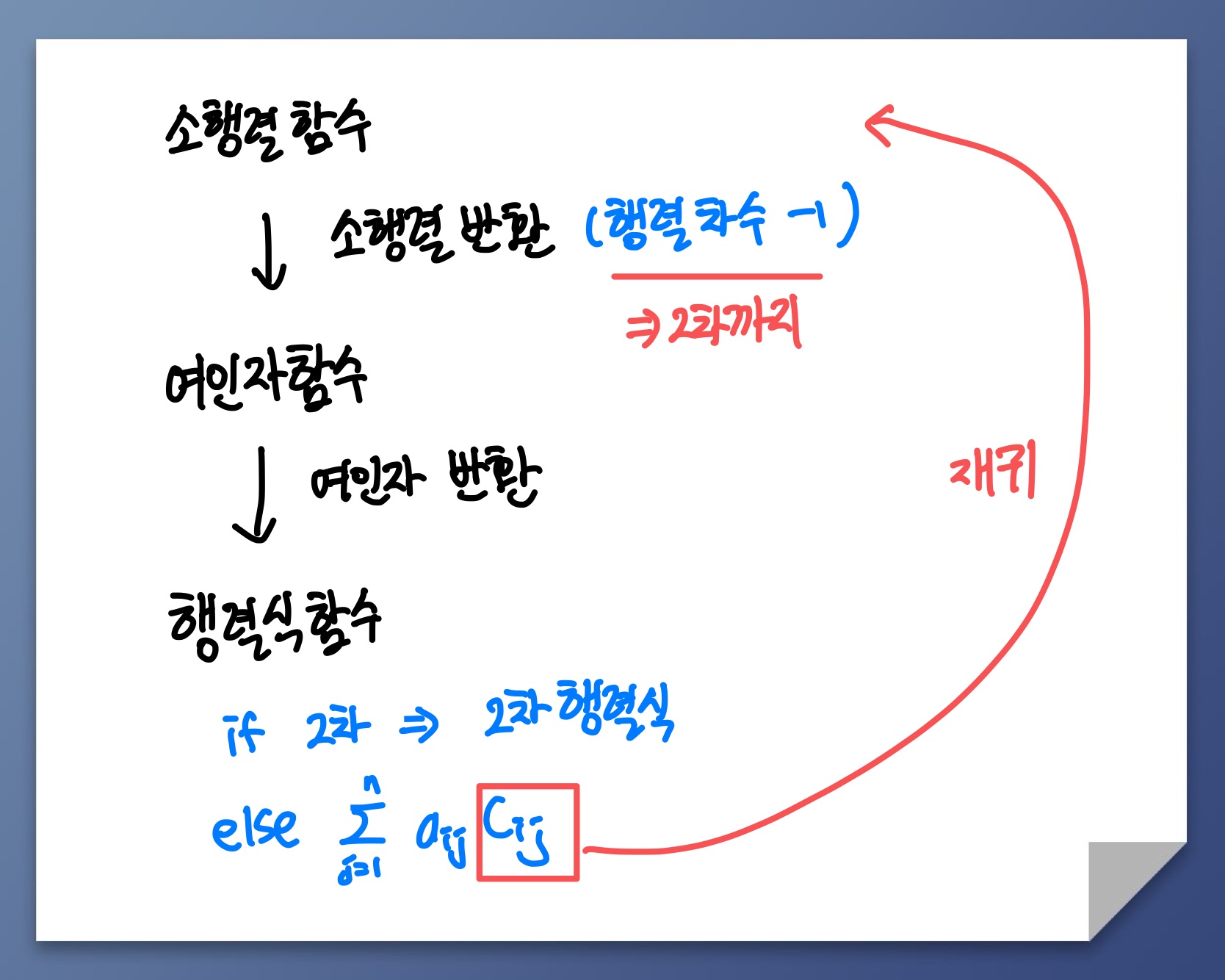
재귀로 한번 표현해보겠다.
import numpy as np
def minor(mat1,i1,j1): # 소행렬식 함수
mat1 = np.delete(mat1, i1, axis = 0)
mat1 = np.delete(mat1, j1, axis = 1)
print(mat1)
return det(mat1,len(mat1))
def cofactor(mat2,i2,j2): # 여인자 함수
return ((-1)**(i2+j2))*minor(mat2,i2,j2)
def det(mat,dim):
if len(mat) == 2: # 2x2 행렬
return (mat[0,0] * mat[1,1]) - (mat[0,1] * mat[1,0])
else :
deter = 0
for i in range (dim):
deter += mat[i,0]*cofactor(mat,i,0) # 재귀
return deter
n = int(input('원하는 차원을 입력해주세요: '))
matrix = np.random.randn(n,n)
print('행렬은: ')
print(matrix)
print(f' 함수를 사용한 행렬식: {det(matrix,n)}')
print(f' 넘파이 내장함수 행렬식: {np.linalg.det(matrix)}')원하는 차원을 입력해주세요: 5 행렬은: [[-0.2801181 0.07610966 -1.44252952 0.83598638 -0.46716956] [ 0.45117994 -0.23642088 0.27426296 0.6262847 0.03535629] [-1.25543968 1.46845358 -1.99691886 -0.60090059 1.39788563] [-0.02833265 -1.65340859 0.60904976 1.36870298 0.64613262] [ 0.2283472 0.78289536 1.53599185 0.51552382 0.1745185 ]] 함수를 사용한 행렬식: 5.411331361128405 넘파이 내장함수 행렬식: 5.41133136112840610을 넣으니깐 컴퓨터가 계산을 못하더라 CPU야 미안해...🥲
내친김에 역함수를 표현하는 함수까지 만들어 보겠다. 아까 코드에서 추가하면 된다.
def inverse_matrix(mat3):
inv_mat = np.zeros([len(mat3),len(mat3)]) # 행렬 틀
for i in range(len(mat3)):
for j in range(len(mat3)):
inv_mat[i,j]= cofactor(mat3,j,i) / det(mat3,len(mat3))
return inv_mat
print('함수를 사용한 역함수')
print(inverse_matrix(matrix))
print('넘파이 내장함수 역함수')
print(np.linalg.inv(matrix))함수를 사용한 역함수 [[ 0.68863033 1.71718346 0.41033622] [-0.12292761 1.87719026 0.5255769 ] [ 1.71733314 2.92042739 3.60484196]] 넘파이 내장함수 역함수 [[ 0.68863033 1.71718346 0.41033622] [-0.12292761 1.87719026 0.5255769 ] [ 1.71733314 2.92042739 3.60484196]]
❗️코딩하다보면 행과 열이 자꾸 헷갈릴수 있는데 중간중간 print 함수로 중간 결과를 계속 확인하면서 코딩하면 시행착오를 덜 겪을 수 있다.
