[LeetCode] 11. Container With Most Water

1. Question

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

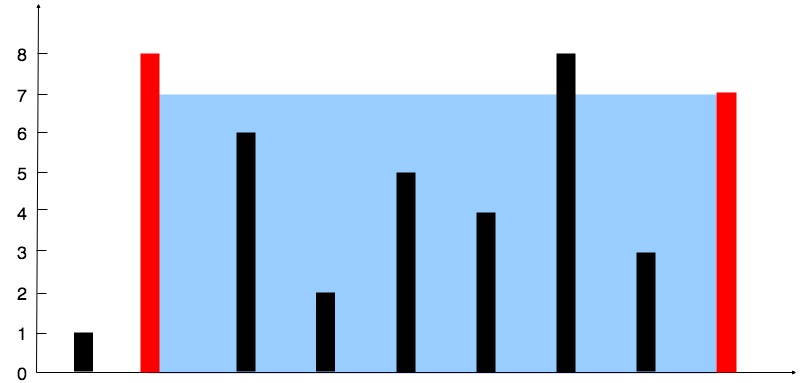
Example 1:

Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49

Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

2. Thoughts

3. Tips learned

4. My solution

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        max_water = 0
        while left < right:
            max_water = max(
                max_water, (right - left) * min(height[left], height[right])
            )
            if height[left] < height[right]:
                for i in range(right - left):
                    if height[left] < height[left + 1]:
                        left += 1
                        break
                    left += 1
            else:
                for i in range(right - left):
                    if height[right] < height[right - 1]:
                        right -= 1
                        break
                    right -= 1
        return max_water

61/61 cases passed (592 ms)
Your runtime beats 88.99 % of python3 submissions
Your memory usage beats 13.67 % of python3 submissions (29.4 MB)

5. AI Solution and Improvements

The given code is a correct solution to the problem, but it can be slightly optimized by removing the inner for loop. You can use an if-else condition to decide whether to increment or decrement the left and right pointers, based on the height of the container walls.

Here's the optimized code:

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left = 0
        right = len(height) - 1
        max_water = 0

        while left < right:
            min_height = min(height[left], height[right])
            max_water = max(max_water, (right - left) * min_height)

            if height[left] < height[right]:
                left += 1
            else:
                right -= 1

        return max_water

In this optimized version, the code simply compares the heights of the left and right walls and moves the pointer that corresponds to the smaller wall. This approach efficiently scans the entire height array once, resulting in a time complexity of ( O(n) ). The space complexity is ( O(1) ) as no additional space is required beyond the input.