[LeetCode] 1466. Reorder Routes to Make All Paths Lead to the City Zero

1. Question

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

Example 1:

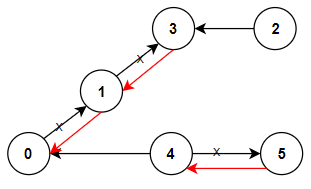
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3:

Input: n = 3, connections = [[1,0],[2,0]]
Output: 0

2. Thoughts

1. Make a graph
2. Use DFS, with the paths that start/end in 0
3. change all DFS paths to head towards 0

3. Tips learned

4. My solution

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        graph = {}
        for i in range(n):
            graph[i] = []
        original = set()
        for dir in connections:
            original.add((dir[0], dir[1]))
            graph[dir[0]].append(dir[1])
            graph[dir[1]].append(dir[0])

        fix = 0
        for path in graph[0]:
            if (0, path) in original:
                fix += 1
            visited = set([0])
            need_visit = deque([path])
            while need_visit:
                city = need_visit.pop()
                if city not in visited:
                    visited.add(city)
                    for new_city in graph[city]:
                        if new_city not in visited:
                            need_visit.append(new_city)
                            if (city, new_city) in original:
                                fix += 1

        return fix

76/76 cases passed (1034 ms)
Your runtime beats 59.73 % of python3 submissions
Your memory usage beats 85.31 % of python3 submissions (43.9 MB)

5. AI Solution and Improvements

Your solution for finding the minimum number of road reorientations needed so that every city can reach the capital (city 0) is on the right track. However, there are a few optimizations and improvements that can be made to enhance its efficiency:

1. Graph Representation: Your graph representation is fine. You have represented it as an adjacency list, which is a good choice for this problem.

2. Initial Road Directions: Storing the original direction of roads in a set (original) is a smart move as it provides O(1) lookup time to check if a road is in its original direction.

3. DFS Implementation: You are using a depth-first search (DFS) algorithm to traverse the graph, which is appropriate. However, your implementation can be more streamlined.

4. Avoiding Redundant Visits: Your current implementation checks and adds cities to visited in different parts of the loop. This can be made more efficient.

Here's an optimized version of your solution:

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        # Construct the graph and keep track of original directions
        graph = {i: [] for i in range(n)}
        original = set()
        for a, b in connections:
            original.add((a, b))  # Store original direction
            graph[a].append(b)     # Outgoing edge from a
            graph[b].append(a)     # Incoming edge to a (for reverse check)

        def dfs(city, visited):
            changes = 0
            visited.add(city)
            for neighbor in graph[city]:
                if neighbor not in visited:
                    # If current direction is the original, we need a change
                    if (city, neighbor) in original:
                        changes += 1
                    changes += dfs(neighbor, visited)
            return changes

        # Starting DFS from the capital
        return dfs(0, set())

In this version, the DFS function is implemented recursively, which simplifies the code. It traverses each city and counts the number of changes needed if the current edge is in the original direction. The visited set ensures that each city is only visited once, reducing redundant checks.