[LeetCode] 437. Path Sum III

1. Question

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Example 1:

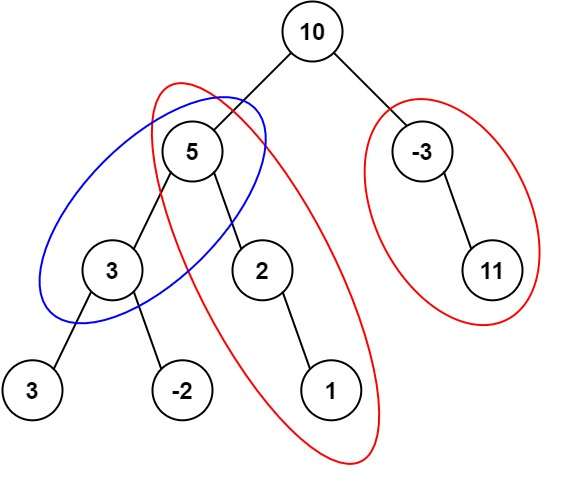
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.

Example 2:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3

2. Thoughts

3. Tips learned

The reason why cache does not need the nonlocal keyword, but count does, lies in the difference between mutable and immutable data types in Python and how variable assignment works.

Mutable vs Immutable Types

• Immutable Types: These are types whose values cannot be changed. If you try to change the value of an immutable variable, what Python actually does is create a new variable in memory. Examples of immutable types include integers, floats, strings, and tuples. In your case, count is an integer, which is immutable.

• Mutable Types: These are types that can be changed in place without creating a new object. Examples of mutable types include lists, dictionaries, and sets. In your case, cache is a dictionary, which is mutable.

Why cache Works Without nonlocal

• Modification vs Assignment: When you modify a mutable object like a dictionary, you are changing the object itself, not the reference to the object. So, when you update cache inside dfs, you are modifying the same dictionary object that was created in pathSum.

• No New Assignment: Since you are not assigning a new value to cache (you're just modifying its contents), Python doesn't treat it as a new local variable within dfs. It correctly recognizes it as the cache dictionary that was defined in pathSum.

Why count Needs nonlocal

• Immutable Type: When you do something like count += 1, you are actually creating a new integer object because integers are immutable. Python, therefore, treats this as an assignment to a new local variable count in the dfs scope.

• Scope Confusion: Without nonlocal, Python assumes that count in dfs is a different variable from count in pathSum, leading to the UnboundLocalError.

• Using nonlocal: By using nonlocal count, you are explicitly telling Python that when you refer to count in dfs, you mean the count defined in the enclosing scope of pathSum.

In summary, cache works fine without nonlocal because you're modifying the dictionary, not assigning a new dictionary. count needs nonlocal because each assignment to an integer variable is treated as creating a new integer object, thus requiring a declaration to link it to the count in the outer scope.

4. My solution

class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        def dfs(node, target):
            if not node:
                return ([], 0)

            left_list, left_count = dfs(node.left, target)
            right_list, right_count = dfs(node.right, target)

            list = [x + node.val for x in (left_list + right_list)] + [node.val]
            count = left_count + right_count

            if target in list:
                count += list.count(target)

            return (list, count)

        _, count = dfs(root, targetSum)
        return count

128/128 cases passed (153 ms)
Your runtime beats 54.21 % of python3 submissions
Your memory usage beats 26.39 % of python3 submissions (17.8 MB)

5. AI Solution and Improvements

Your solution to find the number of paths in a binary tree that sum up to a target value involves a depth-first search (DFS) with a somewhat complex approach to tracking and counting the sums. While your approach is interesting, it can be significantly optimized both in terms of space and time complexity.

Suggested Improvement

A more efficient approach is to use a recursive DFS function that keeps track of the current path sum and a dictionary to store the number of times each sum has occurred so far. This method is more efficient as it avoids creating and merging lists at each node, which can be costly in terms of time and memory.

Here's the revised code:

class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        self.count = 0
        cache = {0: 1}

        def dfs(node, current_sum):
            if not node:
                return

            # Update the current sum and the number of paths that reach this sum
            current_sum += node.val
            old_sum = current_sum - targetSum
            self.count += cache.get(old_sum, 0)

            # Update the cache with the current sum
            cache[current_sum] = cache.get(current_sum, 0) + 1

            # Recursively call on children
            dfs(node.left, current_sum)
            dfs(node.right, current_sum)

            # Remove the current sum from the cache when going back up the recursion tree
            cache[current_sum] -= 1

        dfs(root, 0)
        return self.count

Explanation

• Recursive DFS: The dfs function traverses the tree, keeping track of the cumulative sum of the node values from the root to the current node.

• Path Sum Counting: When the difference between the current cumulative sum and the target sum has been seen before, it means there's a path that sums up to the target sum. The count of such paths is incremented accordingly.

• Cache: A dictionary (cache) is used to keep track of how many times each sum has occurred. This is crucial for efficiently finding the number of paths that add up to the target sum.

• Updating and Cleaning Up the Cache: After each node visit, the current sum is added to the cache. When the recursion goes back up the tree (after visiting left and right children), the current sum is decremented in the cache to ensure only the sums of the current paths are counted.

Benefits of the Improved Solution

• Efficiency: This approach is more efficient in terms of both time and space. It avoids the overhead of creating and managing lists of sums at each node.
• Simplicity: The logic is simpler and more direct, focusing on the cumulative sums and the differences that match the target sum.
• Scalability: The solution is more scalable and can handle larger trees more effectively.