[LeetCode] 48. Rotate Image

1. Question

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

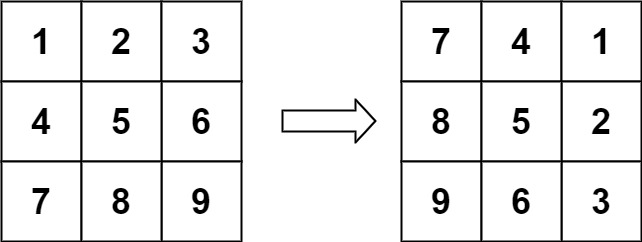
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

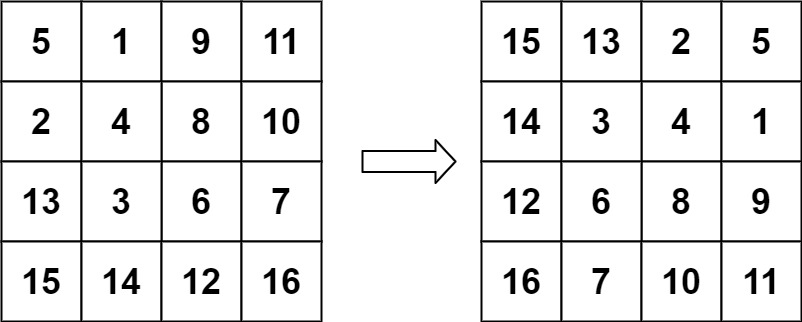
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

2. Thoughts

3. Tips learned

3.1. Transposing Matrix

Transposing a matrix in-place is a bit more involved, especially because it typically applies to square matrices (where the number of rows is equal to the number of columns).
For square matrices, you can perform in-place transposition by swapping elements without using extra space for another matrix. Here's how you can do it in Python:

def transpose_square_matrix_in_place(matrix):
    n = len(matrix)  # Assuming a square matrix
    for i in range(n):
        for j in range(i + 1, n):
            # Swap element at position (i, j) with the element at position (j, i)
            matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

# Example usage:
matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]

transpose_square_matrix_in_place(matrix)
print(matrix)

This code snippet works by looping through elements above the matrix's diagonal and swapping them with their corresponding elements below the diagonal. Note that this method only works for square matrices because of the inherent requirement that the matrix must have the same number of rows and columns for an in-place transpose.

4. My solution

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix[0])
        for i in range(n):
            for j in range(i + 1, n):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

        for i in range(n):
            for j in range(n // 2):
                matrix[i][j], matrix[i][n - 1 - j] = matrix[i][n - 1 - j], matrix[i][j]

21/21 cases passed (40 ms)
Your runtime beats 47.33 % of python3 submissions
Your memory usage beats 65.94 % of python3 submissions (16.6 MB)

5. AI Solution and Improvements

Your solution for rotating an n x n 2D matrix clockwise in-place is correct and follows a two-step process which is both efficient and elegant. Here's a breakdown of what your code does:

1. Transpose the Matrix: The first loop swaps the elements symmetrically along the diagonal, effectively transposing the matrix. In matrix terms, it changes rows to columns and vice versa, which is the first step in rotating the matrix clockwise.

2. Reverse Each Row: The second loop reverses each row of the transposed matrix. Since the transpose step essentially prepares the matrix by aligning elements in a way that they only need to be mirrored horizontally to complete the 90-degree clockwise rotation, reversing each row finalizes this rotation.

Your implementation is efficient, as it operates in-place without needing extra space for another matrix, adhering to the constraint of doing the rotation in-place. However, it's always good to consider code readability and clarity for maintenance and understanding. Here's a slightly refactored version of your solution with added comments for clarity:

class Solution:
    def rotate(self, matrix):
        n = len(matrix)
        # Transpose the matrix
        for i in range(n):
            for j in range(i + 1, n):  # Start from i+1 to avoid re-swapping
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

        # Reverse each row
        for i in range(n):
            matrix[i].reverse()  # More Pythonic way to reverse a list

This version performs the same operations but uses the reverse() method for lists to make the row-reversal step clearer and slightly more Pythonic, though it's a matter of preference.

Additional Considerations

• Code Readability: Including comments or choosing more descriptive variable names can enhance readability without sacrificing efficiency.
• Testing Edge Cases: To ensure robustness, consider edge cases such as an empty matrix or a 1x1 matrix (though the latter behaves correctly under this algorithm).

Your approach efficiently solves the problem with O(1) extra space (not counting the input) and O(n^2) time complexity, which is required for any solution that must touch every element of the matrix. It's a well-known and recommended approach for this problem.