[LeetCode] 52. N-Queens II

1. Question

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example 1:

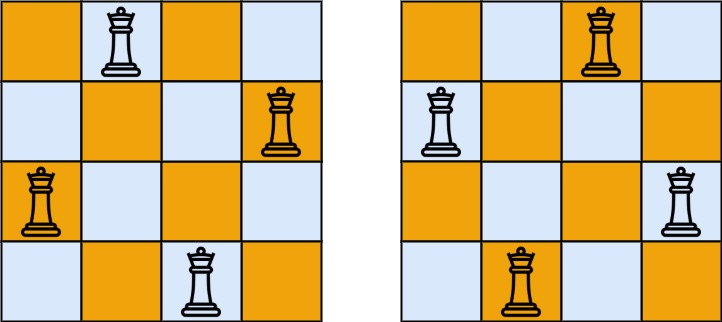
Input: n = 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown.

Example 2:

Input: n = 1
Output: 1

2. Thoughts

divide the expression into left and right.
Using recursion, calculate left and right.
Use Memoization and set conversion for optimization

3. Tips learned

4. My solution

class Solution:
    def is_big (self,x,y,a,b):
        if a > x:
            return True
        elif a == x:
            if b < y:
                return True
        return False

    def removed(self, set_xy,x,y):
        discard_list = set()
        for x_from_set,y_from_set in set_xy:
            if self.is_big(x,y,x_from_set,y_from_set) or x_from_set == x or y_from_set ==y or abs(y-y_from_set) == abs(x-x_from_set):
                discard_list.add((x_from_set,y_from_set))
        return set_xy - discard_list

    def select_possible(self,set_xy,n,trial):
        if n == trial:
            return len(set_xy)
            
        count = 0
        for x,y in set_xy:
                count += self.select_possible(self.removed(set_xy,x,y),n,trial+1)
        return count

    def totalNQueens(self, n: int) -> int:
        set_xy = set((x,y) for x in range(n) for y in range(n))
        return self.select_possible(set_xy,n,1)

8/8 cases passed (1201 ms)
Your runtime beats 5.01 % of python3 submissions
Your memory usage beats 21.00 % of python3 submissions (16.82 MB)

5. AI Solution and Improvements