[LeetCode / C++] 289. Game of Life

Leetcode Question Link

1. Question

According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.

Example 1:

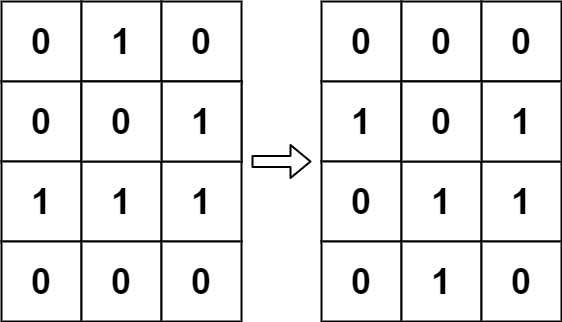
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

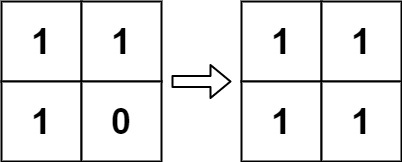
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

2. Thoughts

// @problem define
// 1. under population (cel == 1 && nb <2)
// 2. live (cel == 1 && 2 <= nb <= 3)
// 3. over population (cel == 1 && 3 < nb)
// 4. reproduction (cel == 0 && nb == 3 )
// 5. Try to solve it in place!

// @algorithm
// To remain both current state and next state,
// we can set as alive-> dead : -1 // dead-> alive: 3
// that way, we can keep on track on both current and next state.
// Then, we can go over again and change the board.

// @ How-to
// Use 3 functions:
// 1. check neighbor live num
//  ==> check nb if not out of bound.
// 2. check next state
//  ==> if 0/1, use switch statement for 1.
// 3. finalize the board

// @ complexity
// O(n) tc/sc

3. Tips learned

No External help this time.

4. My solution

#include <iostream>
#include <vector>

using namespace std;

class Solution
{
public:
    void liveOrDie(int i, int j, vector<vector<int>> &board, int alive)
    {
        // alive -> dead : 3
        if (board.at(i).at(j) >= 1 && (alive < 2 || alive > 3))
        {
            board.at(i).at(j) = 3;
        }

        // dead -> alive : -1
        else if (board.at(i).at(j) <= 0 && alive == 3)
        {
            board.at(i).at(j) = -1;
        }
    }

    int numOfAliveNeighbor(int i, int j, vector<vector<int>> &board)
    {
        int alive = 0;
        for (int k = -1; k <= 1; k++)
        {
            for (int l = -1; l <= 1; l++)
            {
                if ((k == 0 && l == 0) || i + k < 0 || j + l < 0 || i + k >= board.size() || j + l >= board.at(i).size())
                    continue;
                if (board.at(i + k).at(j + l) >= 1)
                    alive++;
            }
        }
        return alive;
    }

    void finalizeBoard(int i, int j, vector<vector<int>> &board)
    {
        if (board.at(i).at(j) == 3)
            board.at(i).at(j) = 0;
        else if (board.at(i).at(j) == -1)
            board.at(i).at(j) = 1;
    }

    void gameOfLife(vector<vector<int>> &board)
    {
        for (int i = 0; i < board.size(); i++)
        {
            for (int j = 0; j < board.at(i).size(); j++)
            {
                int alive = numOfAliveNeighbor(i, j, board);
                liveOrDie(i, j, board, alive);
            }
        }

        for (int i = 0; i < board.size(); i++)
        {
            for (int j = 0; j < board.at(i).size(); j++)
            {
                finalizeBoard(i, j, board);
            }
        }
    }
};

23/23 cases passed (0 ms)
Your runtime beats 100 % of cpp submissions
Your memory usage beats 55.87 % of cpp submissions (8.5 MB)

5. AI Solution and Improvements

Your implementation is clear and works well for the given problem. I have a few suggestions to improve the performance and simplify the code:

Suggested Improvements:

1. Combine liveOrDie and finalizeBoard Logic:
   You can reduce the number of iterations over the board. Currently, the board is iterated twice—once for updating the states and once for finalizing them. By storing both current and next states in the same cell, you can do the updates in a single iteration.

   To achieve this, use bitwise operations to encode the current and next states. For example:

   • Use the least significant bit (LSB) for the current state.
   • Use the second least significant bit for the next state.

   Here's how you can modify the values:

   • If the cell is alive and stays alive, set it to 3 (11 in binary, LSB remains 1, next state is 1).
   • If the cell is alive and dies, set it to 1 (01 in binary).
   • If the cell is dead and stays dead, set it to 0.
   • If the cell is dead and becomes alive, set it to 2 (10 in binary).

   After updating all cells, shift the bits to get the final state.

2. Optimize Neighbor Counting:
   You can simplify the neighbor counting logic to reduce the overhead. Instead of multiple if checks in numOfAliveNeighbor, you can use bounds-checking at the beginning and iterate only the valid neighbors.

Optimized Code Example:

#include <iostream>
#include <vector>

using namespace std;

class Solution
{
public:
    void gameOfLife(vector<vector<int>> &board)
    {
        int rows = board.size();
        int cols = board[0].size();
        
        // Directions array to check all 8 neighbors
        vector<pair<int, int>> directions = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};
        
        // First pass: compute next state and store it in the second bit
        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < cols; j++)
            {
                int aliveNeighbors = 0;

                // Count alive neighbors
                for (auto &dir : directions)
                {
                    int ni = i + dir.first;
                    int nj = j + dir.second;
                    if (ni >= 0 && ni < rows && nj >= 0 && nj < cols && (board[ni][nj] & 1))
                    {
                        aliveNeighbors++;
                    }
                }

                // Apply the rules by setting the 2nd bit
                if ((board[i][j] & 1) && (aliveNeighbors == 2 || aliveNeighbors == 3))
                {
                    board[i][j] |= 2; // Cell remains alive
                }
                else if (!(board[i][j] & 1) && aliveNeighbors == 3)
                {
                    board[i][j] |= 2; // Cell becomes alive
                }
            }
        }

        // Second pass: finalize the board state
        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < cols; j++)
            {
                board[i][j] >>= 1; // Update to the next state
            }
        }
    }
};

Explanation:

1. Bitwise Encoding:

   • The first bit (board[i][j] & 1) represents the current state.
   • The second bit (board[i][j] & 2) represents the next state.

2. Directions Array:

   • The directions vector is used to simplify neighbor traversal.

3. Single Pass Update:

   • In the first pass, the next state is calculated and stored using bitwise OR (|= 2).
   • In the second pass, the entire board is updated by right-shifting each cell (>>= 1).

Benefits of This Approach:

• In-Place Update: The board is updated in place without using extra space.
• Reduced Complexity: Only two passes are needed, which improves efficiency.
• Simplified Logic: Bitwise operations make it easy to store both current and future states in the same cell.

Let me know if you need further explanation or additional help with this optimization!