[SW Expert Academy] 1248. Common Ancestor

1. Question

Write a program to find the nearest common ancestor of any two vertices in a binary tree and determine the size of the subtree rooted at that vertex.

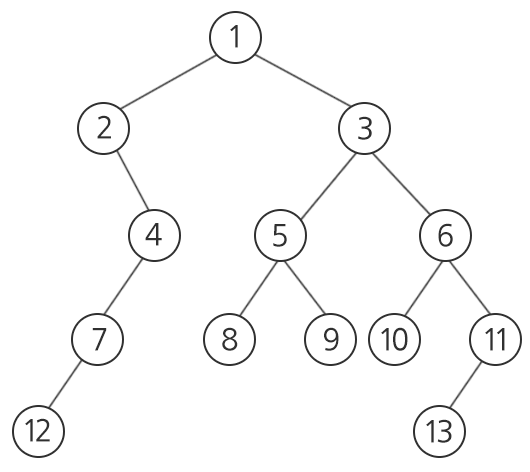
For example, in the above binary tree, vertices 8 and 13 have two common ancestors, vertices 3 and 1. Among them, the closest to vertices 8 and 13 is vertex 3, and the size of the subtree rooted at vertex 3 (the number of vertices included in the subtree) is 8.

[Input]

The number of test cases is given in the first line.

For each case, the first line provides the number of vertices V (10 ≤ V ≤ 10000), the number of edges E, and two vertex numbers for finding the common ancestor.

In the second line of each case, E edges are listed. Edges are always marked in the order of “parent child”.

In the tree mentioned above, the edge connecting vertices 5 and 8 is marked as “5 8”.

The vertex numbers are integers from 1 to V, and the root vertex is always number 1.

[Output]

For each test case, print '#t' (where t is the test case number starting from 1), and then print the number of the nearest common ancestor and the size of the subtree rooted at it, separated by a space.

2. Thoughts

1. Make tree using Dictionary. Add parent node to the first element of the tree
   ex) tree[2] = [1,3,4] when 2 is the parent to 3 and 4, and 1 is the parent to 2
2. get lowest parent by using the first element and back-tracing the parents. Find the first element that co-exists
3. get subtree of that parent node using recursion

3. Tips learned

4. My solution

def make_tree(nodes):
    tree = {i: [] for i in range (1,N+1)}
    tree[1].append(0)
    for node in range(N-1):
        parent = int(nodes[node*2])
        child = int(nodes[node * 2 +1])

        # Add at the 0th index to go back up
        tree[child] = [parent] + tree[child]
        tree[parent].append(child)
    return tree

def get_lowest_tree(tree):
    first_stack = []
    second_stack = []
    first_it , second_it = first,second

    while True:
        # print(first_it)
        first_it = tree[first_it][0]
        first_stack.append(first_it)
        if first_it == 1:
            break
        
    
    while True:
        second_it = tree[second_it][0]
        second_stack.append(second_it)
        if second_it == 1:
            break
        
    parent_node = 0
    
    if len(first_stack) >= len(second_stack):
        first_set = set(first_stack)
        for stack in second_stack:
            if stack in first_set:
                parent_node = stack
                break
    
    else:
        second_set = set(second_stack)
        for stack in first_stack:
            if stack in second_set:
                parent_node = stack
                break
    
    return parent_node

def get_subtree_size(tree,parent):
    right_size, left_size = 0,0
    if len(tree[parent]) == 1:
        return 1
    elif len(tree[parent]) == 2: 
        right_size = get_subtree_size(tree, tree[parent][1])
    else:
        right_size = get_subtree_size(tree, tree[parent][1])
        left_size = get_subtree_size(tree, tree[parent][2])

    return 1+right_size + left_size


T = int(input())

for test_case in range(1, T + 1):
    N, E, first, second = map(int, input().split()) 
    nodes = input().split()

    tree = make_tree(nodes)
    lowest_parent = get_lowest_tree(tree)
    size = get_subtree_size(tree,lowest_parent)
    
    print(f"#{test_case} {lowest_parent} {size}")

5. AI Solution and Improvements

Your solution for finding the nearest common ancestor and the size of the subtree in a binary tree is well-structured and appears to address the problem effectively. However, there are a few improvements and optimizations that can be made:

1. Optimizing make_tree Function: The way you're constructing the tree is good, but it can be made more efficient. Instead of using a list for every node, you can use a dictionary to store child nodes, which might speed up the process of finding children.

2. Improving get_lowest_tree Function: Your approach to finding the lowest common ancestor (LCA) is based on traversing from the nodes up to the root and then finding the common node. This is a bit inefficient as it involves unnecessary traversals. You can optimize it using a recursive approach to find the LCA directly, reducing the time complexity.

3. Optimizing get_subtree_size Function: The current implementation of this function is recursive, which is fine, but you might want to consider memoization to avoid recalculating subtree sizes.

4. Handling Input and Output: Your current handling of input and output seems appropriate for the problem statement.

Here's an improved version of your code with these considerations:

def make_tree(nodes, N):
    tree = {i: {'parent': None, 'children': []} for i in range(1, N+1)}
    for i in range(0, len(nodes), 2):
        parent, child = int(nodes[i]), int(nodes[i+1])
        tree[child]['parent'] = parent
        tree[parent]['children'].append(child)
    return tree

def find_LCA(tree, node1, node2):
    ancestors = set()
    while node1:
        ancestors.add(node1)
        node1 = tree[node1]['parent']
    while node2 not in ancestors:
        node2 = tree[node2]['parent']
    return node2

def get_subtree_size(tree, node, memo):
    if node in memo:
        return memo[node]
    size = 1  # Count current node
    for child in tree[node]['children']:
        size += get_subtree_size(tree, child, memo)
    memo[node] = size
    return size

T = int(input())
for test_case in range(1, T + 1):
    N, E, first, second = map(int, input().split())
    nodes = input().split()

    tree = make_tree(nodes, N)
    lowest_parent = find_LCA(tree, first, second)
    size = get_subtree_size(tree, lowest_parent, {})

    print(f"#{test_case} {lowest_parent} {size}")

This code addresses the inefficiencies in the original code and should perform better, especially for larger trees.