Graph?
컴퓨터 과학에서 이야기하는 그래프는 일반적으로 내가 알고있는 그래프랑 달랐다. 그 주주죽 선이 그어지는 그래프가 아니라, 점끼리 이어져있는 복잡한 네트워크 망과 같은 이미지다.
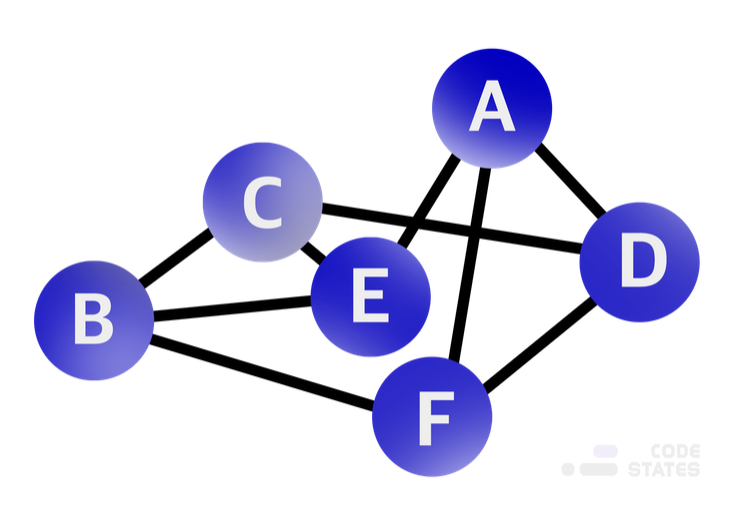
그래프는 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조다. 서로 다른 점들이 직접적인 관계를 가지고 있다면 바로 이어주는 선이 존재하고, 간접적인 관계를 가지고 있다면 다른 여러 점을 거쳐서 이어지는 선이 존재할 수 있다. 여기서 이야기하는 점은 그래프에서는 정점(vertex)라고 표현하고, 선은 간선(edge)라고 표현한다.
쉽게 말하면 그래프라는 것은 연관된 데이터들을 이어서 관계를 가지고 있는 정보를 나타낼 수 있는 자료구조다.
그래프의 실사용 예제
우리가 매일같이 그래프라는 자료구조를 사용하고 있는데, 이건 단순히 데이터 구조로만 생각하면 어렵다. 예를 들어보면 포털 사이트의 검색엔진, SNS, 네비게이션(길찾기) 등에서 사용되는 자료구조가 바로 그래프다. 여기서 더 나아가면, 넷플릭스 추천시스템이나 유사데이터를 보여주는 연관검색어까지도 적용될 수 있다. 물론 거기에는 추가적으로 데이터 보정이 들어가겠지만, 가장 핵심적인 내용은 '그래프'일 것이다.
서울에 사는 A는 부산에 사는 B와 오랜 친구 사이입니다. 이번 주말에 B의 결혼식이 있다고 하여 A는 차를 몰고 부산으로 가려고 합니다. 마침, 대전에 살고 있는 A와 B의 친구 C도 참석을 한다고 하여 A는 대전에서 C를 태워 부산으로 이동을 하려고 합니다.
위는 네비게이션이 구현되는 방식을 가지고 길을 찾는 이야기를 꺼내보았다. 위의 예제에는 3개의 정점이 존재하는데, 각각 A, B, C가 사는 도시들을 각각의 그래프 정점(vertex)로 대입할 수 있다. 그리고 이 3개의 정점은 서로 이어지는 간선(관계)를 가지고 있다.
- 정점 : 서울, 대전, 부산
- 간선 : 서울ㅡ대전 , 대전ㅡ부산, 부산ㅡ서울
위에서 볼 수 있듯, 서울, 대전, 부산 간의 이동경로는 간선이 된다. 이 간선은 이동할 수 있음이라는 관계를 표시한다. 정점에 만약에 캐나다의 토론토나 미국의 뉴욕을 추가할 수는 있지만, 자동차로 이동할 수 없기때문에 어떤 간선도 생길 수 없다. 그래프에서 이것은 관계가 없다.고 이야기한다. 간선은 이동할 수 있다는 관계만 알려줄 뿐 가까운지 먼지, 연관된 정보는 없는지에 대한 이야기가 없기때문에 연결 강도에 대한 판단을 할 수 없어서비가중치 그래프라고 한다.let isConnected = { seoul: { busan: true, daejeon: true }, daejeon: { seoul: true, busan: true }, busan: { seoul: true, daejeon: true } } console.log(isConnected.seoul.daejeon) // true console.log(isConnected.daejeon.busan) // true
코드로 나타내면 다음과 같다. 하지만 지금의 정보로는 연결되어있는지 안되어있는지에 대한 정보만 있기때문에 네비게이션의 기능을 할 수 있도록 자료구조를 수정한다면 거리나 방향을 표시해서 가중치 그래프로 표현할 수 있다. 그렇게 함으로서 비로소 관계성을 가지고 있는 가중치 그래프가 될 수 있다.
추가적으로 이야기한 SNS의 경우, 무향그래프의 경우에는 페이스북의 친구관계(양방향 관계성)와 유향그래프의 경우에는 인스타그램의 팔로우관계(일방향 관계성)을 예를 들 수 있다. 넷플릭스나 왓챠플레이의 추천시스템은 아마도 A유저가 좋아하는 목록들과 B유저가 좋아하는 목록을 엮어서 서로에게 연관된 영화를 추천할 수 있는 방식으로 되어있을 것이기 때문에 일종의 그래프 데이터일 것이라고 추측한다.(나중에 알게되겠지만..)
그래프의 표현 방식 : 인접 행렬 & 인접 리스트
인접행렬
앞서 그래프의 관계성을 보면 간선이 연결되어있는 것으로 표현을 했는데, 이것을 인접한다라고 이야기한다. 인접 행렬은 정점들끼리 인접하고 있는 정보를 알려주는 행렬으로 2차원 배열의 모습을 가지고 있다. 무향 그래프의 경우 행과 열에 모두 1로 표시가 되고, 유향그래프의 경우 행(from) 렬(to)에서 to 방향에 1이 있게 된다. 만약에 관계성이 있는 가중치 그래프라고하면 굳이 1이라는 연결 표시가 아니라 거리값 그자체가 할당되어있을 수 있다.
언제 인접행렬을 쓸까?
- 한개의 큰 표와 같은 모습을 한 인접행렬은 두 정점사이의 관계가 있는지 없는지 확인할때 용이하다.
- i에서 j로 진출하는 간선 matrix[i][j]
- 가장 빠른 경로를 찾을 때, 간선 수 계산을 통해서 정답을 구할 수 있다.(혹은 거리값을 더해서)
인접 리스트?
인접행렬의 한 행을 가져다 놓은 것이라고 보면 편하다. 그냥 어디에 연결되어있는지를 빠르게 확인하기 위한 정보다. 만약에 정점별로 우선 순위가 있다면 우선 순위별로 정렬해서 담아서 사용하면된다. 만약 없다면 그냥 리스트를 그대로 가져다 쓰면 된다.
- 우선순위와 관련된 정보는 인접리스트보다 queue와 heap을 사용해야한다.
인접 리스트는 언제 사용하면 좋을까?
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장한다.
- 서로 인접하지 않다면 0을, 인접하다면 1을 저장하기때문에 메모리를 많이 차지한다.
- 메모리를 효율적으로 사용하고 싶다면 인접 행렬대신 리스트를 사용한다.
Tree?
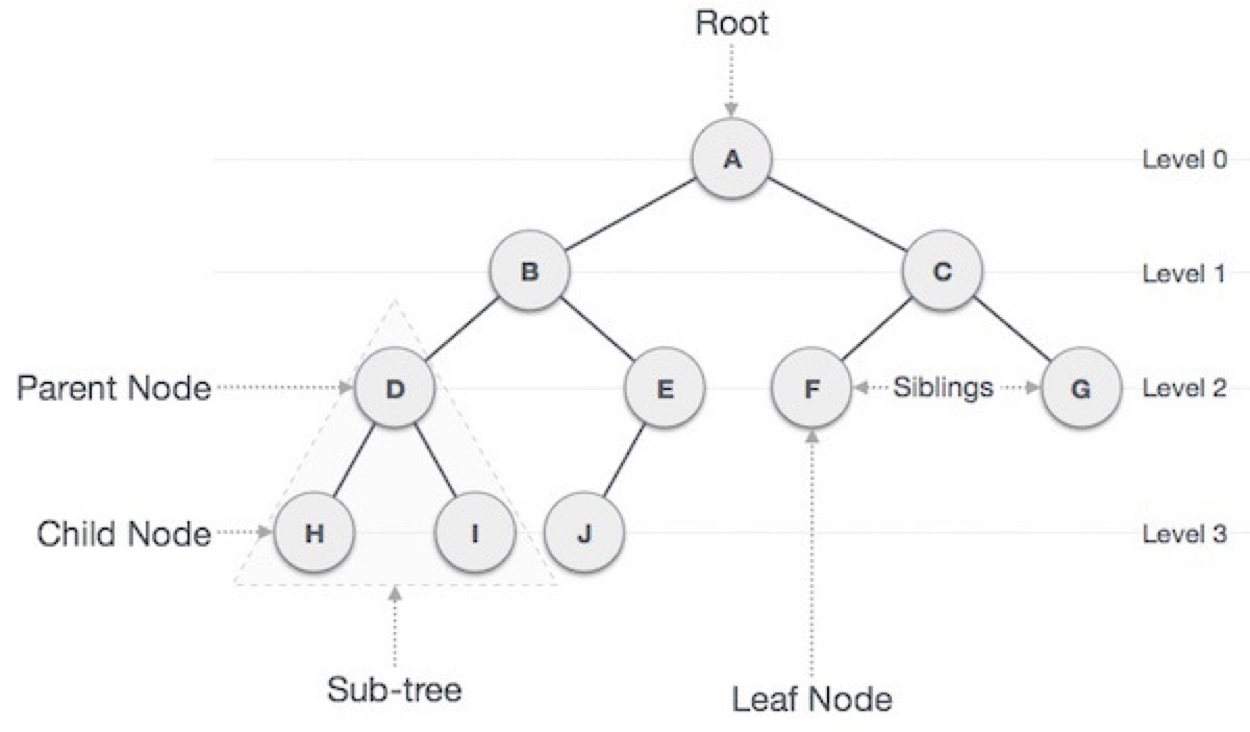
트리구조는 그래프의 여러 구조중에 일방향 그래프의 한 종류다. 따지고 보면 그냥 그래프인데 밑으로만 뻗어나가는 것이다. 생성되는 모양이 거꾸로된 나무와 비슷해서 트리구조라고 부른다. Tree Tree Tree
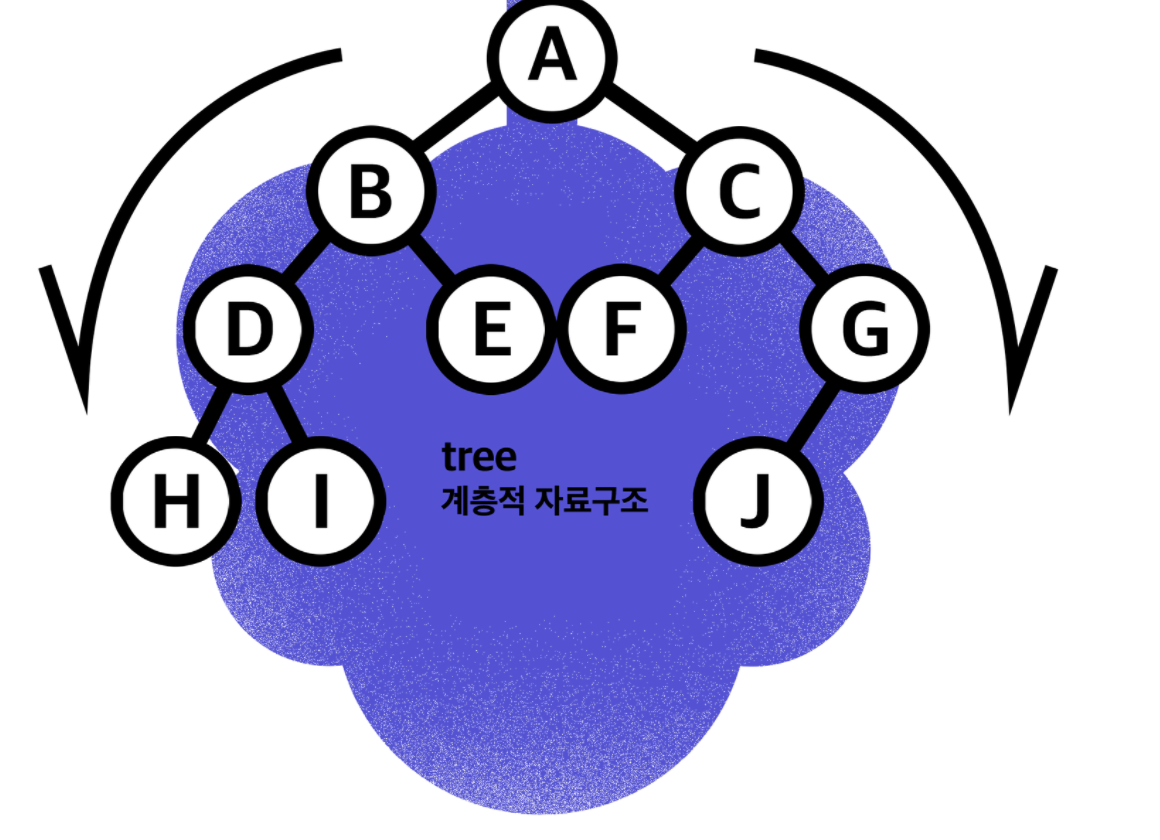
일종의 가계도 처럼 생겼는데, 데이터가 바로 아래에 있는 하나 이상의 데이터에 단방향으로 연결되는 계층적 자료구조라고 할 수 있다. 내가 사용하고 있는 맥의 파일시스템 역시 이러한 트리구조로 이루어져있다. 데이터를 순차적으로 나열시킨 형태인 선형구조가 아닌, 하나의 데이터 뒤에 여러개의 데이터가 존재할 수 있는 비선형 구조로 되어 있고, 계층적으로 표현이 되며 아래로만 뻗기 때문에 사이클이 없다.(밑으로만 간다.)
Tree Structure
Root : 루트는 꼭대기에 있는 꼭짓점 데이터다. 여러개의 간선으로 데이터를 연결한다.
Node : 각 데이터가 매달려 있는 정점(vertex)
상위노드와 하위노드 : 위에 달린놈이 부모 노드, 아래달린놈이 자식 노드
자식없는 노드 : 리프 노드!!!!!
동일한 깊이의 노드들:형제자매 노드!
Height(높이) : 루트부터 가장 안쪽에 있는 노드까지의 레벨
Depth(깊이) : 특정노드부터 루트까지의 레벨
트리 일부를 떼오면 Subtree(서브트리)라고 부른다.
Tree구조 실사용 예제
언뜻 보아도 눈에 익숙한 이 자료구조의 형태는 구조를 표현하는 데에 초점이 맞춰져 있기 때문에 주변에서 알게 모르게 많이 접했다. 사람이 사용하기 편리하기 위해, 쓰기 좋기 위해 만들어진 자료구조이기 때문이다.
가장 대표적으로, 컴퓨터의 디렉토리 구조를 생각할 수 있다. 어떠한 프로그램이나 파일을 찾을 때 우리는 우리만의 방식으로 잘 정돈된 폴더에서 타고 들어가 원하는 것을 찾게 된다. 혹은, 이미 만들어 놓은 폴더 구조(예시로, C:/kimcoding/document/따오기/참새)에서 찾고는 한다. 모두 하나의 폴더에서 시작되어, 가지처럼 뻗어나가는 형태를 보이고 있다.
마치며
자료구조중에 제일 어려웠던 그래프를 정리했다. 이 부분에서 명확하지 않은 부분이 많아서 헷갈렸는데 관계성과 순서와 관련된 정보를 담고있다는 식으로 이해하면 좀 빠를 듯 하다.
