BS 알고리즘(Binary algorithm)

시작하기전에

알고리즘 이야기를 시작하기전에, 이전의 Binary Search Tree와는 결이 다른 이야기라는 것을 먼저 밝힌다. 엄연히 말하면 위의 BST는 Tree, 즉 자료구조형인데 이진법을 채택해서 Tree 구조를 구현하는 한 형태를 이르는 말이고 BS알고리즘은 이진법을 이용해서 데이터를 찾는 알고리즘을 포괄하는 말이다. 구조의 형태와 알고리즘의 중심적인 컨셉은 같지만 이건 엄연히 알고리즘이고 위에 BST는 엄연히 자료구조의 한 형식일 뿐이다. BST구조는 BS알고리즘을 이용한다는 성립하지 않음을 먼저 밝힌다.

Binary Search Tree - 이진법으로 데이터를 분류해서 Tree형태로 구축한 자료구조
Binary Search Algorithm - input range를 줄이면서 원하는 result를 찾기위한 알고리즘

이진탐색 알고리즘이란?(Binary Search)

이진탐색이란 데이터가 정렬되어있는 배열에서 특정한 값을 찾아내는 알고리즘이다. 배열의 중간에 있는 임의의 값을 선택해서 찾고자하는 값 target과 비교한다. target이 중간 값보다 작으면 중간 값을 기준으로 좌측의 데이터들을 대상으로, target이 중간값보다 크면 배열의 우측을 대상으로 다시 탐색한다.

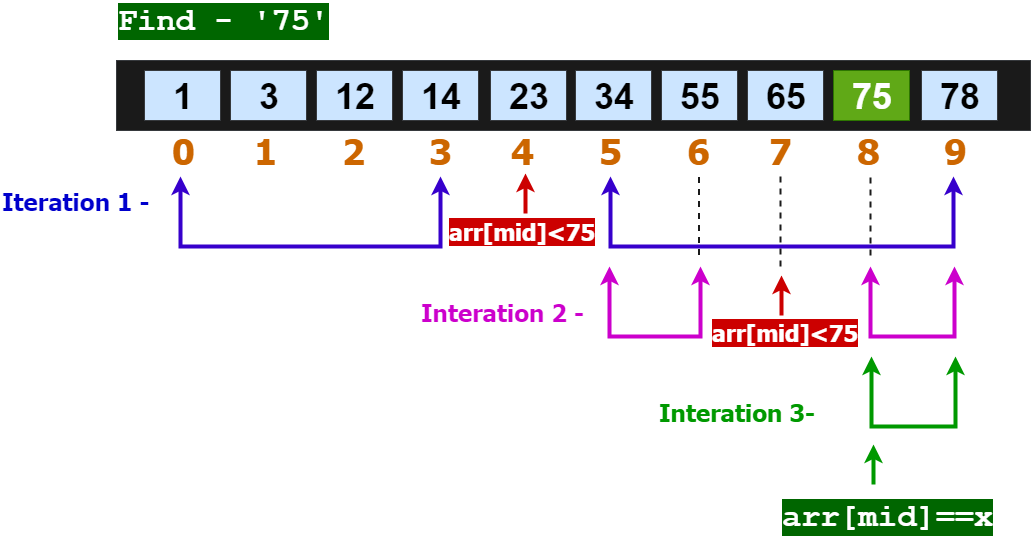
이걸 말로 풀면 너무 길어져서 이해가 어려워지는데 그림을 보면 조금은 이해가 쉽다. Find - '75'는 찾아야 될 값 75를 나타낸다. 위와 같이 9개의 배열이 있을 때 75를 찾기위해 순차적으로 찾게 되면 최대 9번의 순회를 지나야 한다. 여기서는 9번이니까 그냥 순차적으로 찾아도, 금방 찾을 수 있겠지만 늘 그렇듯 알고리즘은 최악의 케이스가 있다고 생각해야한다. 예를 들어 배열이 9개가 아니고 9999조개가 된다고 생각해보면, 그게 아무리 컴퓨터라고 해도 골이 아플정도로 오래 걸릴 것이다. 위에서보면 색깔별로 range가 줄어드는 것을 확인할 수 있는데 이를 이용해서 탐색범위를 1/2로 줄여버리는 것이다.

가장 중요한 조건은 모든 데이터는 순차적으로 있어야 한다는 것이다.
왜냐하면, 데이터를 탐색하는 과정이 비교를 이용하기 때문이다. 그것이 인스턴스로 내부에 다른 값이 있다면 그 값을 순차적으로 정렬시켜야하고, 배열안의 배열이라면 배열 속의 배열값자체를 sort시켜야 한다는 말이다.

Blue Interaction - 1

1차시 비교단계다. 최소값과 최댓값(시작점과 끝점이 아니라, 내가 잡을 수 있는 최소와 최대의 범위)에서 중간값을 만들어내고 그 값과 비교해서 크다면 오른쪽 범위를 선택하고, 작다면 왼쪽 범위를 선택한다.

Purple Interaction - 2

2차시 비교단계다. 역시 동일하게 중간값을 찾아서 그 값보다 크면 오른쪽, 작다면 왼쪽을 선택한다.
.
.
.
최종적으로는 최소범위, 최대범위 혹은 중간값중에 target과 같은 경우를 찾아서 데이터 서칭을 마치게 된다. 최대 9번, 최소 8번은 찾아야했던 절차를 3번으로 줄여버렸으니 획기적이지 않을 수 없다. 물론 나중에 더 복잡하고 어렵고 획기적인 알고리즘을 만날 수도 있겠지만 우선 여기에서 크게 재미를 느꼈었다.

이진탐색 알고리즘 예제로 확인하기

탈출조건에 대한 issue