Diffusion model (DDPM) network 구현

KIMHYUNSU·2025년 1월 20일

Diffusion model 을 더욱 잘 이해하기 위해 구현된 코드를 살펴보았다.

https://www.kaggle.com/code/brighalot/diffusion-model-u-net/edit
kaggle을 참고했습니다.

Forward

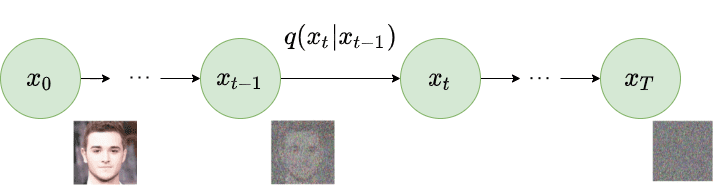
데이터를 노이즈화하는 수학적 변환 과정으로 이해하자.

Forward 과정의 본질

Forward 과정의 목표는 원본 데이터 $x_0$ 를 점진적으로 노이즈화하여 $x_t$ 를 생성하는 것
이 과정에서 특정한 블록을 통과하거나 학습이 필요 없음.
Forward 과정은 수학적으로 정의된 식에 따라 진행
$[ x_t = \sqrt{\bar{\alpha}_t} \cdot x_0 + \sqrt{1 - \bar{\alpha}_t} \cdot \epsilon ]$
- $\sqrt{\bar{\alpha}_t}$ : $t$ 에서 원본 데이터가 얼마나 얼마나 유지되는지의 비율.
- $\sqrt{1 - \bar{\alpha}_t}$
- $\epsilon$ : 가우시안 노이즈.

노이즈화

입력 데이터에 가우시안 노이즈를 추가하여 t에서의 노이즈화된 데이터를 생성

시간 단계별 변환

t마다 노이즈의 비율이 증가하고 원본 데이터의 비율이 감소

Forward 과정을 담당하는 함수

# DDPM noise schedule 생성
b_t = (beta2 - beta1) * torch.linspace(0, 1, timesteps + 1, device=device) + beta1
a_t = 1 - b_t
ab_t = torch.cumsum(a_t.log(), dim=0).exp()    
ab_t[0] = 1

def perturb_input(x, t, noise):
    return ab_t.sqrt()[t, None, None, None] * x + (1 - ab_t[t, None, None, None]) * noise

원본 데이터 $x_0$ 에 $\sqrt{\bar{\alpha}_t}$ ( == ab_t)를 곱하여 조정.

가우시안 노이즈 $\epsilon$ 에 $\sqrt{1 - \bar{\alpha}_t}$ 를 곱하여 조정.

두 결과를 합산하여 $x_t$ 생성.

x :

원본 데이터 $x_0$

텐서 크기 : (N, C, H, W)

배치크기 N, 채널 수 C, 높이 H, 너비 W

t :

시간 t

텐서 크기 : (N, none, none, none)

배치크기와 동일

noise

$x_0$ 에 추가할 가우시안 노이즈

텐서 크기 : (N, C, H, W)

Reverse

필요한 block들을 먼저 정의

각각 reverse 과정에서 사용하게될 블록들

전반적으로 U-net 구조를 따른다.

ResidualConvBlock

class ResidualConvBlock(nn.Module):
    def __init__(self, in_channels: int, out_channels: int, is_res: bool = False) -> None:
        """
        잔차 컨볼루션 블록 초기화.
        - in_channels: 입력 채널 수
        - out_channels: 출력 채널 수
        - is_res: 잔차 연결 여부를 나타내는 플래그
        """
        super().__init__()

        # 입력과 출력 채널 수가 같은지 확인 (잔차 연결을 위해 필요)
        self.same_channels = in_channels == out_channels

        # 잔차 연결 여부 플래그
        self.is_res = is_res

        # 첫 번째 컨볼루션 레이어 (3x3 커널, 스트라이드 1, 패딩 1)
        self.conv1 = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, 3, 1, 1),   # 컨볼루션 레이어
            nn.BatchNorm2d(out_channels),                    # 배치 정규화
            nn.GELU(),                                       # GELU 활성화 함수
        )

        # 두 번째 컨볼루션 레이어 (3x3 커널, 동일 설정)
        self.conv2 = nn.Sequential(
            nn.Conv2d(out_channels, out_channels, 3, 1, 1),
            nn.BatchNorm2d(out_channels),
            nn.GELU(),
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """
        입력 텐서 x를 처리하여 출력 텐서를 반환.
        - x: 입력 텐서 (N, C, H, W)
        """
        if self.is_res:  # 잔차 연결을 사용할 경우
            x1 = self.conv1(x)  # 첫 번째 컨볼루션 레이어
            x2 = self.conv2(x1)  # 두 번째 컨볼루션 레이어
            
            if self.same_channels:  # 입력과 출력 채널 수가 같다면 직접 잔차 연결
                out = x + x2
            else:  # 입력과 출력 채널 수가 다르면 1x1 컨볼루션으로 차원 조정 후 잔차 연결
                shortcut = nn.Conv2d(x.shape[1], x2.shape[1], 1).to(x.device)
                out = shortcut(x) + x2
            return out / 1.414  # 출력값 정규화

        else:  # 잔차 연결을 사용하지 않는 경우
            x1 = self.conv1(x)
            x2 = self.conv2(x1)
            return x2

U-Net의 기본 블록

입력 데이터 특징 추출

잔차 연결(Residual Connection)을 포함 -> 학습 안정성을 유지

2개의 컨볼루션 레이어:

Conv2d: 3x3 커널, 스트라이드 1, 패딩 1.

BatchNorm2d: 배치 정규화.

GELU: 활성화 함수로 비선형성을 추가.

잔차 연결 (옵션):

is_res=True인 경우, 입력 $x$ 와 출력 $x_2$ 를 더해 정보를 보존

입력 텐서 $x$ 를 두 개의 컨볼루션 레이어를 통과, 필요시 잔차 연결을 적용하여 출력 생성 $[\text{output} = x + x_2]$

Unet

UnetDown (DownSampling)

class UnetDown(nn.Module):
    def __init__(self, in_channels, out_channels):
        """
        다운샘플링 블록 초기화.
        - in_channels: 입력 채널 수
        - out_channels: 출력 채널 수
        """
        super(UnetDown, self).__init__()

        # 잔차 컨볼루션 블록과 MaxPooling으로 구성된 레이어
        layers = [
            ResidualConvBlock(in_channels, out_channels),  # 잔차 컨볼루션 블록
            ResidualConvBlock(out_channels, out_channels),  # 추가 잔차 컨볼루션 블록
            nn.MaxPool2d(2),  # 2x 다운샘플링
        ]
        self.model = nn.Sequential(*layers)

    def forward(self, x):
        """
        입력 텐서를 다운샘플링하여 반환.
        """
        return self.model(x)

U-Net의 다운샘플링 블록으로, 고해상도 입력 데이터를 저해상도 특징으로 변환합니다.

입력 데이터의 공간 크기를 줄이며, 특징 정보를 압축합니다.

2개의 ResidualConvBlock:

입력 데이터를 처리하여 특징을 추출.

MaxPool2d:

2x 다운샘플링을 수행하여 공간 해상도를 줄임.

입력 데이터를 잔차 블록으로 처리한 뒤, MaxPooling으로 공간 크기를 줄입니다.
출력 특징 맵: $[ \text{output} = \text{MaxPool}(\text{ResidualConv}(x)) ]$

UnetUp (Upsampling)

class UnetUp(nn.Module):
    def __init__(self, in_channels, out_channels):
        """
        업샘플링 블록 초기화.
        - in_channels: 입력 채널 수
        - out_channels: 출력 채널 수
        """
        super(UnetUp, self).__init__()

        # 업샘플링과 잔차 컨볼루션 블록으로 구성된 레이어
        layers = [
            nn.ConvTranspose2d(in_channels, out_channels, 2, 2),  # 전치 컨볼루션으로 업샘플링
            ResidualConvBlock(out_channels, out_channels),        # 잔차 컨볼루션 블록
            ResidualConvBlock(out_channels, out_channels),        # 추가 잔차 컨볼루션 블록
        ]
        self.model = nn.Sequential(*layers)

    def forward(self, x, skip):
        """
        업샘플링 과정을 수행.
        - x: 업샘플링할 텐서
        - skip: U-Net의 skip 연결에서 전달된 텐서
        """
        x = torch.cat((x, skip), 1)  # 채널 차원에서 결합
        return self.model(x)

U-Net의 업샘플링 블록으로, 저해상도 특징 맵을 고해상도로 복원합니다.

U-Net의 skip 연결을 사용하여 다운샘플링 과정에서 얻은 고해상도 정보를 재활용합니다.

ConvTranspose2d:

전치 컨볼루션으로 2x 업샘플링을 수행.

2개의 ResidualConvBlock:

업샘플링된 데이터를 추가적으로 처리하여 고해상도 특징을 복원.

입력 텐서 x 와 skip 연결 텐서 skip 을 채널 차원에서 결합: $[ x = \text{cat}(x, \text{skip}, \text{dim}=1) ]$

결합된 텐서를 업샘플링과 잔차 블록을 통해 처리하여 최종 출력 생성.

EmbedFC

class EmbedFC(nn.Module):
    def __init__(self, input_dim, emb_dim):
        """
        입력 데이터를 임베딩 공간으로 변환하는 레이어.
        - input_dim: 입력 데이터의 차원
        - emb_dim: 출력 임베딩 차원
        """
        super(EmbedFC, self).__init__()

        # FC 레이어로 구성된 임베딩 네트워크
        layers = [
            nn.Linear(input_dim, emb_dim),  # 첫 번째 FC 레이어
            nn.GELU(),                     # 활성화 함수
            nn.Linear(emb_dim, emb_dim),   # 두 번째 FC 레이어
        ]
        self.model = nn.Sequential(*layers)

    def forward(self, x):
        """
        입력 텐서를 임베딩 공간으로 변환.
        """
        x = x.view(-1, self.input_dim)  # 입력 텐서를 평탄화
        return self.model(x)

t 와 조건 정보 ( c )를 저차원 임베딩으로 변환하여 모델에 입력

Diffusion 모델에서 시간 단계와 조건을 효과적으로 학습하기 위해 필요

2개의 Linear 레이어:

입력 데이터를 두 번의 선형 변환으로 처리.

GELU:

첫 번째 Linear 레이어와 두 번째 Linear 레이어 사이에 비선형성을 추가.

입력 데이터 x를 flatten하고 선형 레이어를 통과하며 임베딩 벡터를 생성:

[ \text{ output} = \text{ Linear }(\text{ GELU }(\text{ Linear }( x ))) ]

최종 Unet

아래 그림의 ddpm 의 구조를 참고했다.

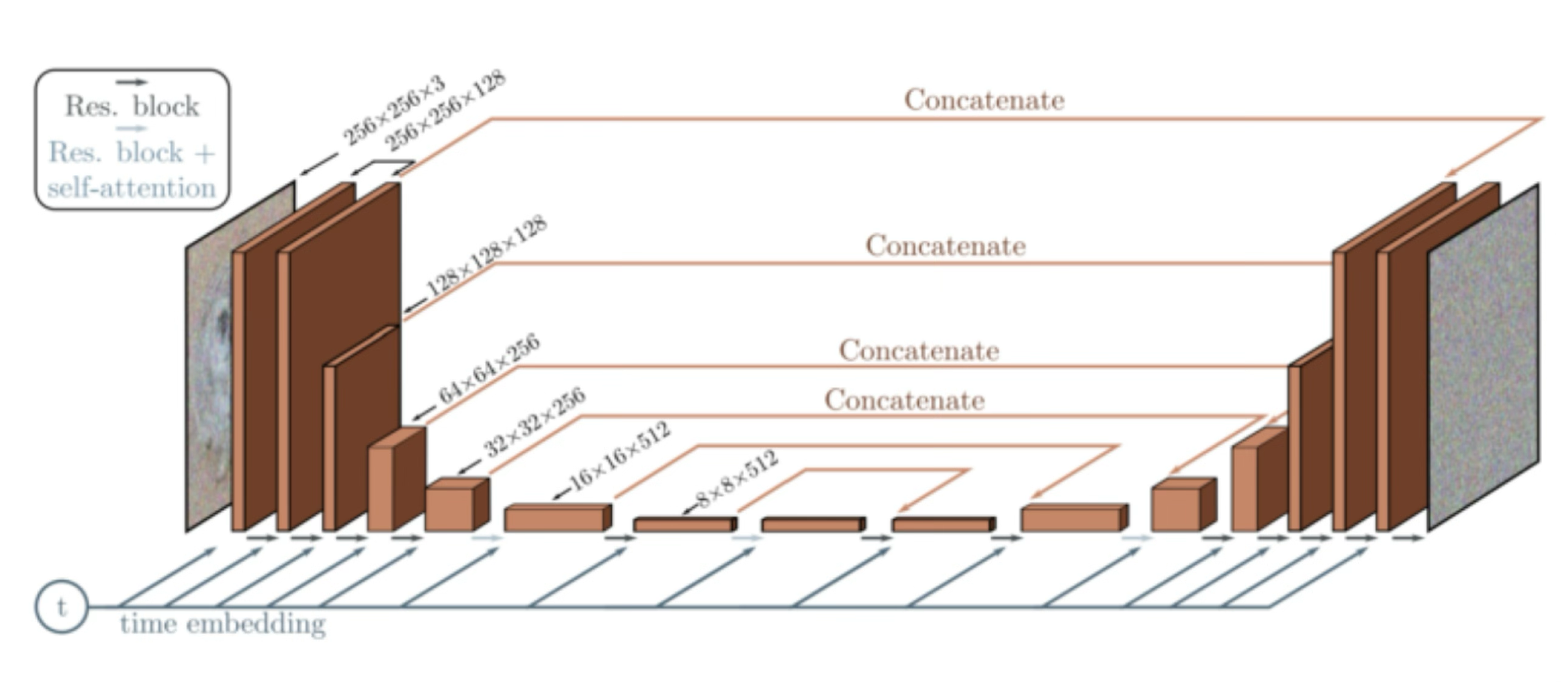
class ContextUnet(nn.Module):
    def __init__(self, in_channels, n_feat=256, n_cfeat=10, height=256):  # cfeat - context features
        """
        ContextUnet 초기화 함수.
        - in_channels: 입력 이미지의 채널 수 (예: RGB라면 3)
        - n_feat: 중간 단계의 특징 맵 채널 수 (기본값: 256)
        - n_cfeat: 컨텍스트 벡터의 크기 (조건부 학습에 사용)
        - height: 입력 이미지의 높이 (가로 세로가 같아야 하며, 4로 나누어떨어져야 함)
        """
        super(ContextUnet, self).__init__()

        # 입력 채널, 중간 단계 특징 채널 수, 컨텍스트 벡터 크기, 이미지 높이
        self.in_channels = in_channels
        self.n_feat = n_feat
        self.n_cfeat = n_cfeat
        self.h = height  # 가로와 세로가 동일하다고 가정. (4로 나누어떨어져야 함, 예: 256, 128, 64, ...)

        # 초기 컨볼루션 레이어 정의 (첫 번째 ResidualConvBlock)
        self.init_conv = ResidualConvBlock(in_channels, n_feat, is_res=True)

        # 다운샘플링 경로 정의 (UnetDown 블록 추가)
        self.down1 = UnetDown(n_feat, n_feat)         # 다운샘플링 1단계: 256 -> 128
        self.down2 = UnetDown(n_feat, 2 * n_feat)     # 다운샘플링 2단계: 128 -> 64
        self.down3 = UnetDown(2 * n_feat, 4 * n_feat) # 다운샘플링 3단계: 64 -> 32
        self.down4 = UnetDown(4 * n_feat, 8 * n_feat) # 다운샘플링 4단계: 32 -> 16
        self.down5 = UnetDown(8 * n_feat, 8 * n_feat) # 다운샘플링 5단계: 16 -> 8

        # Bottleneck 처리: 특징 맵을 벡터로 변환
        self.to_vec = nn.Sequential(nn.AvgPool2d((8)), nn.GELU())  # 크기를 1x1로 줄임

        # 시간 단계(timestep)와 컨텍스트(context) 임베딩을 위한 fully connected 레이어
        self.timeembed1 = EmbedFC(1, 16 * n_feat)  # 시간 임베딩 1
        self.timeembed2 = EmbedFC(1, 8 * n_feat)   # 시간 임베딩 2
        self.contextembed1 = EmbedFC(n_cfeat, 16 * n_feat)  # 컨텍스트 임베딩 1
        self.contextembed2 = EmbedFC(n_cfeat, 8 * n_feat)   # 컨텍스트 임베딩 2

        # 업샘플링 경로 정의 (UnetUp 블록 추가)
        self.up1 = UnetUp(16 * n_feat, 8 * n_feat)  # 업샘플링 1단계: 8 -> 16
        self.up2 = UnetUp(16 * n_feat, 4 * n_feat)  # 업샘플링 2단계: 16 -> 32
        self.up3 = UnetUp(8 * n_feat, 2 * n_feat)   # 업샘플링 3단계: 32 -> 64
        self.up4 = UnetUp(4 * n_feat, n_feat)       # 업샘플링 4단계: 64 -> 128
        self.up5 = UnetUp(2 * n_feat, n_feat)       # 업샘플링 5단계: 128 -> 256

        # 최종 출력 레이어 (입력 이미지와 동일한 채널 수로 매핑)
        self.out = nn.Sequential(
            nn.Conv2d(2 * n_feat, n_feat, 3, 1, 1),  # 채널 수 축소 (3x3 컨볼루션)
            nn.GroupNorm(8, n_feat),                 # 그룹 정규화
            nn.ReLU(),                               # 활성화 함수
            nn.Conv2d(n_feat, self.in_channels, 3, 1, 1),  # 입력 채널 수와 동일하게 출력 (예: RGB라면 3)
        )

    def forward(self, x, t, c=None):
        """
        Forward 함수. 입력 데이터를 처리하여 노이즈를 예측.
        - x : (batch, n_feat, h, w): 입력 이미지 (batch 크기, 채널 수, 높이, 너비)
        - t : (batch, n_cfeat): 시간 단계 (timestep) (조건부 Diffusion에서 사용)
        - c : (batch, n_classes): 컨텍스트 레이블 (예: 클래스 조건)
        """

        # 1. 입력 이미지를 초기 컨볼루션 레이어에 통과
        x = self.init_conv(x)  # 첫 번째 ResidualConvBlock

        # 2. 다운샘플링 경로를 따라 데이터 처리
        down1 = self.down1(x)       # 다운샘플링 1단계: 256 -> 128
        down2 = self.down2(down1)   # 다운샘플링 2단계: 128 -> 64
        down3 = self.down3(down2)   # 다운샘플링 3단계: 64 -> 32
        down4 = self.down4(down3)   # 다운샘플링 4단계: 32 -> 16
        down5 = self.down5(down4)   # 다운샘플링 5단계: 16 -> 8

        # 3. 특징 맵을 벡터로 변환
        hiddenvec = self.to_vec(down5)  # Bottleneck 단계

        # 4. 컨텍스트가 없는 경우, 기본값으로 0 벡터를 생성
        if c is None:
            c = torch.zeros(x.shape[0], self.n_cfeat).to(x)  # 크기: [batch, n_cfeat]

        # 5. 시간 임베딩 및 컨텍스트 임베딩 계산
        cemb1 = self.contextembed1(c).view(-1, 16 * self.n_feat, 1, 1)  # [batch, 16 * n_feat, 1, 1]
        temb1 = self.timeembed1(t).view(-1, 16 * self.n_feat, 1, 1)     # [batch, 16 * n_feat, 1, 1]
        cemb2 = self.contextembed2(c).view(-1, 8 * self.n_feat, 1, 1)   # [batch, 8 * n_feat, 1, 1]
        temb2 = self.timeembed2(t).view(-1, 8 * self.n_feat, 1, 1)      # [batch, 8 * n_feat, 1, 1]

        # 6. 업샘플링 경로를 따라 데이터 복원
        up1 = self.up1(cemb1 * hiddenvec + temb1, down5)  # 업샘플링 1단계
        up2 = self.up2(up1, down4)                        # 업샘플링 2단계
        up3 = self.up3(up2, down3)                        # 업샘플링 3단계
        up4 = self.up4(up3, down2)                        # 업샘플링 4단계
        up5 = self.up5(up4, down1)                        # 업샘플링 5단계

        # 7. 최종 출력 레이어를 통과하여 노이즈 예측 결과 생성
        out = self.out(torch.cat((up5, x), 1))  # Skip Connection 결합 후 출력

        return out

U-Net의 전체 구조를 정의, 시간 정보 $t$ 와 조건 정보 $c$ 를 통합

downsample -> bottlenack -> upsample

다운샘플링:

UnetDown 블록을 사용해 입력 이미지를 저해상도로 변환.

임베딩:

EmbedFC를 사용해 $t$ 와 $c$ 를 임베딩하여 모델에 전달.

업샘플링:

UnetUp 블록을 사용해 저해상도 특징을 복원.

skip 연결을 통해 다운샘플링 과정의 고해상도 정보를 재활용.

최종 출력:

입력과 동일한 해상도와 채널 수로 복원.

[ \epsilon_\theta(x_t, t, c) ]

블록 이름	역할	주요 기능
ResidualConvBlock	특징 추출 및 잔차 연결 지원	2개의 컨볼루션 레이어와 BatchNorm, GELU 활성화 포함
UnetDown	입력 데이터를 다운샘플링하여 저해상도 특징 추출	잔차 블록과 MaxPooling 포함
UnetUp	저해상도 특징을 고해상도로 복원	전치 컨볼루션과 잔차 블록 포함
EmbedFC	시간 단계 $t$ 와 조건 정보 $c$ 를 임베딩	선형 변환과 GELU 활성화 사용
ContextUnet	U-Net 구조를 정의하며 $t, c$ 를 통합	다운샘플링 → 임베딩 → 업샘플링

학습

nn_model = ContextUnet(in_channels=3, n_feat=n_feat, n_cfeat=n_cfeat, height=height).to(device)

dataset = CustomDataset("/kaggle/input/pixel-art/sprites.npy", "/kaggle/input/pixel-art/sprites_labels.npy", transform, null_context=False)
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=1)
optim = torch.optim.Adam(nn_model.parameters(), lr=lrate)

kaggle에서는 pixel-art 데이터셋으로 진행했다.
이미지 사이즈가 16x16 이다.
그래서 kaggle 코드는 height = 16으로 설정하고 네트워크 구조도 조금 더 단순하게 구현되어있다.

사용하려는 데이터셋 이미지 사이즈가 256이라면 256으로 설정해주면 될 것 같다.

# hyperparameters

# diffusion hyperparameters
timesteps = 500
beta1 = 1e-4
beta2 = 0.02

# network hyperparameters
device = torch.device("cuda:0" if torch.cuda.is_available() else torch.device('cpu'))
n_feat = 64 # 64 hidden dimension feature
n_cfeat = 5 # context vector is of size 5
height = 16 # 16x16 image
save_dir = '/kaggle/working/'

# training hyperparameters
batch_size = 100
n_epoch = 50
lrate=1e-3

나중에 다른 데이터셋을 넣어서 진행해보면 좋을 거 같다.

# 모델을 학습 모드로 설정
nn_model.train()

# 전체 학습 에포크 반복
for ep in range(n_epoch):  # n_epoch: 총 학습 에포크 수
    print(f'epoch {ep}')  # 현재 에포크 출력
    
    # 학습률을 선형적으로 감소시키는 코드
    optim.param_groups[0]['lr'] = lrate * (1 - ep / n_epoch)
    # 초기 학습률 lrate에 대해, 현재 에포크(ep)가 진행될수록 학습률을 점차 줄임.
    # (1 - ep/n_epoch)는 에포크의 진행 비율에 따른 가중치.

    # dataloader에서 미니배치 단위로 데이터를 반복
    pbar = tqdm(dataloader, mininterval=2)  # tqdm은 진행 상황을 시각적으로 보여줌
    for x, _ in pbar:   # x: 배치 단위 이미지, _는 라벨
        # 옵티마이저의 이전 기울기 초기화
        optim.zero_grad()  # 이전 배치의 기울기를 지움
        
        # 입력 데이터를 GPU로 이동 (device는 'cuda' 또는 'cpu')
        x = x.to(device)
        
        # Forward 과정: 입력 데이터에 노이즈 추가
        noise = torch.randn_like(x)  # 입력 데이터와 동일한 크기의 가우시안 노이즈 생성
        t = torch.randint(1, timesteps + 1, (x.shape[0],)).to(device)  
        # 각 배치에 대해 랜덤한 시간 단계 t 선택 (1부터 timesteps까지)
        
        x_pert = perturb_input(x, t, noise)  
        # perturb_input 함수로 노이즈 추가
        # x_pert = sqrt(α_t_bar) * x + sqrt(1 - α_t_bar) * noise
        # Forward 과정에서 t 단계의 노이즈화된 데이터 x_t 생성

        # Reverse 과정: 네트워크를 사용하여 노이즈 복원
        pred_noise = nn_model(x_pert, t / timesteps)  
        # x_t와 정규화된 시간 단계 t/timesteps를 네트워크에 전달
        # nn_model은 ContextUnet 클래스의 객체로, 입력된 x_t에서 노이즈를 예측

        # 손실 함수 계산 (예측된 노이즈와 실제 노이즈 간의 MSE)
        loss = F.mse_loss(pred_noise, noise)
        # F.mse_loss: 평균 제곱 오차(MSE)를 계산
        # 실제 노이즈와 모델이 예측한 노이즈의 차이를 최소화하는 방향으로 학습
        
        loss.backward()  
        # 역전파(Backpropagation)를 통해 손실 함수의 기울기를 계산
        # 이 과정에서 모델의 모든 가중치에 대해 기울기가 계산됨
        
        optim.step()  
        # 옵티마이저를 사용해 모델의 가중치를 업데이트
        # 계산된 기울기를 기반으로 가중치를 조정하여 손실을 최소화

# 학습된 모델을 주기적으로 저장
torch.save(nn_model.state_dict(), save_dir + f"model.pth")
# 모델의 가중치와 상태를 저장
print('saved model at ' + save_dir + f"model.pth")