[자연어처리] N-Gram Smoothing

KIMHYUNSU·2025년 4월 16일

Backoff Interpolation Katz Backoff Laplace smoothing N-Gram Smoothing NLP add-k stupid backoff

NLP

목록 보기

12/22

ch06-1. N-Gram Smoothing

test할때
training 에 frequency 가 0 이어서
(나오지 않았던 단어)

test할 때, training 에 존재하지 않는 단어 (frequency 가 0)
이 probability 를 곱하면 확률이 0이 되므로
- 특정 확률값을 갖게해서 곱하면 되지 않을까?
- 자주 등장하는 단어의 frequency 를 나눠갖자..
보통 bigram에서 적용하도록 구현함..

Laplace smoothing

모든 count 에 1을 더해주는 것

기존에는 특정 단어가 나올 카운트(c)를 모든 단어의 수(N)로 나눠 계산했음

그렇게 하지 말고 count 하나는 무조건 있다고 가정
- c_i + 1
- 1씩 모든 단어들이 카운트가 하나씩 생겼기 때문에 N에V를 더한 값으로 나눠주면 됨

Example

트레이닝에 hot 이 counting 이 안 됨
→ hot 이 카운팅이 많이 되도록 해야함
→ hot 을 만들어주고 1을 더함

1을 더해주지 않으면 hot 은 항상 0이됨
그래서 그것을 방지하고자 1을 다 더해줌
- bigram 도 1을 더해줌

seoul 을 모든 unigram 에 다 더해줌
이 과정에서 빈도가 원래 0이었던 gram(단어)도 1이 됨으로써,
기존에는 등장하지 않았던 단어들도 최소한의 확률을 가질 수 있게 됨.
```
결과적으로 테이블의 크기가 증가하게 됨.
```

여기서 V는 number of task (4)

Add-One Smoothing은 간단하면서 직관적인 방법이지만, 현실적으로는 지나치게 단순한 경향이 있음.
특히 단어 수(Vocabulary Size)가 많으면 매우 큰 크기의 데이터가 만들어지며, 실제 확률 분포를 왜곡할 수 있음.
빈도가 낮은 단어에 대해 과도한 확률을 할당하게 되면서 모델의 성능이 오히려 떨어지는 경우가 발생할 수 있음.

Add-K smoothing

1이 너무 커서 영향을 너무 많이 준다면…

count 에다가 1이 아니라 k 값을 더해줌

0.5, 0.05, 0.01 ...
그래서 계산할 때도 c(count) + k를 N+kV 로 나눠줌
- bigram도 마찬가지..
- 여기서도 V는 number of task (4)

validation set
training corpus → k 값을 변형해가면서 하이퍼파라미터 튜닝 (val set 을 가지고)

만약에 더 advance하면?

Interpolation, Backoff

smoothing 테크닉을 요즘엔 사실 잘 안 씀..

둘 다 제일 중요하게 생각해야하는 건 
higher order gram value 를 lower order gram value 에 전달해주는... 그런 개념

Interpolation

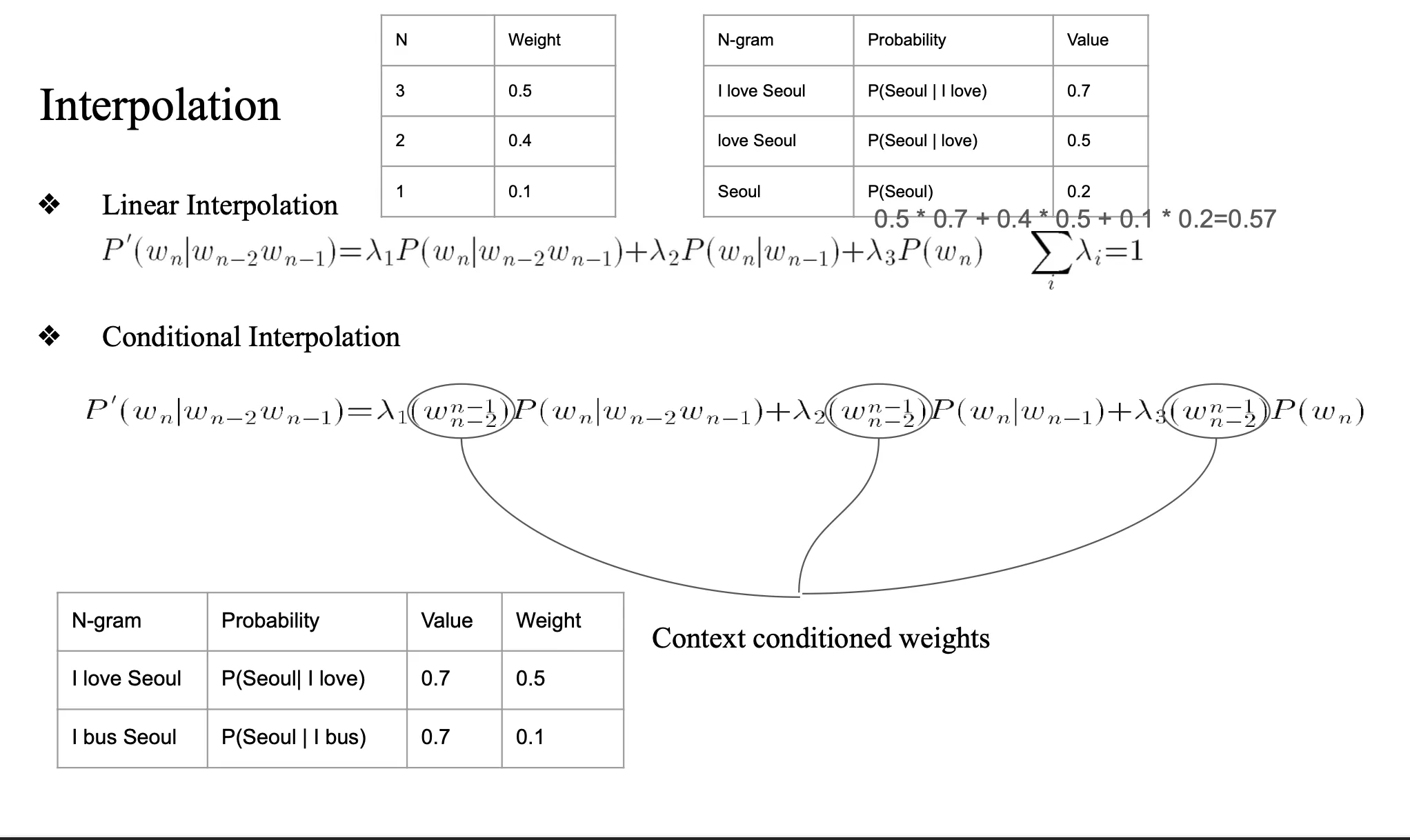
여러 n-gram 모델의 확률 값을 선형 결합(linear combination) 하여 사용
하위 n gram 모두 고려하는 방법

λ1, λ2, λ3은 가중치이고, 모두 양수이며 합이 1이 되게 설정함.
높은 차수의 n-gram 정보가 없더라도 낮은 차수의 모델이 뒷받침해주는 역할을 함.
항상 모든 모델(n-gram들)을 동시에 사용함.

linear
- 선형적으로 결합
- value들(가중치)을 고정된 값으로 미리 세팅 -> validation 이후 직접 수정
conditional
- validation set을 보고 통계값으로 람다를 미리 세팅해놓음
- 실제 성능이 더 좋음

Backoff

높은 차수의 n-gram 모델에서 확률을 추정할 수 없는 경우, 더 낮은 차수의 모델로 되돌아가서(back off) 추정하는 방식

높은 차수 -> 낮은 차수에 물려주기

높은 n gram과 낮은 n gram 들의 확률 값들을 계속 물려주는 것

예: 3-gram P(w3 | w1, w2) 가 없으면 → P(w3 | w2)로 backoff
	그것도 없으면 → P(w3)로 backoff

두가지 개념 중요
- higher n gram 이 0 일때 lower order n gram 을 이용
- higher n order 의 값을 lower order 에게 나눠주는 개념

Katz Backoff

높은 차수 n-gram을 먼저 시도함 (예: P(w3 | w1, w2))
해당 n-gram이 관측되지 않았다면, 한 단계 낮은 차수의 n-gram로 backoff함 (P(w3 | w2))
이때 낮은 차수 n-gram의 확률에 α를 곱해서 조정된 확률을 얻음
α는 높은 차수에서 할인된 확률 질량을 적절히 나눠주는 역할을 함

알파를 구해서… 계산에 활용

→ higher order n gram prob 을 깎아서 lower order n gram 에 적용

우리는 P(sushi | i eat)을 구하려고 함.
그런데 count(i eat sushi) = 0이므로, 기본 n-gram 모델에서는 확률이 0이 되어버림.
→ 이런 경우를 방지하기 위해 Katz Backoff를 사용함.

주어진 값:

P(hamburgers | i eat) = 0.5
P(pizza | i eat) = 0.4
P(sushi) = 0.3
P(sushi | eat) = 0.6
P(sushi | i eat) → 없음 (count = 0)
Discount factor = 0.9

P_BO(sushi | i eat)를 Katz Backoff로 계산하라.

Step 1: 관측된 n-gram에 대한 할인 적용

관측된 것들만 discount 적용

P'(hamburgers | i eat) = 0.5 × 0.9 = 0.45
P'(pizza | i eat) = 0.4 × 0.9 = 0.36
남은 확률 mass = 1 - (0.45 + 0.36) = 0.19

이 0.19가 unseen 후보들에게 분배될 확률 질량임. 이때 Katz Backoff에서는 이 질량을 lower-order 확률을 기반으로 나눔.

Step 2: sushi는 관측되지 않았으므로 backoff

sushi는 P(sushi | i eat) 없음 → backoff → P(sushi | eat) = 0.6 있음 →

→ 아래와 같이 계산함:

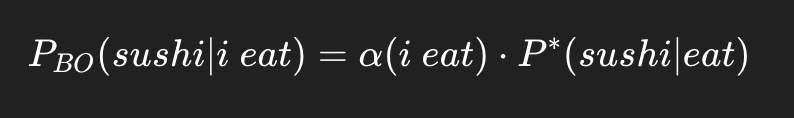
여기서 핵심은: P^*(sushi | eat)를 써도 되느냐?
관측됐으므로, 이 확률도 discount해서 써야 함.

`P(sushi | eat) = 0.6`

→ P^*(sushi | eat) = 0.6 × 0.9

Step 3: α(i eat)를 구한다

α는 "남은 확률 질량 0.19를 lower-order 후보들에게 어떻게 나눌까" 결정하는 계수임.

하나의 unseen 후보 sushi만 있다고 하면 (즉, sushi만 backoff 대상이라면):

(1 - 0.36 - 0.45) = alpha(i eat) * p(sushi | eat)

최종 정리

→ 이 값은 P(sushi | i eat)가 없어서 backoff한 결과고,
→ lower-order 확률(P(sushi | eat))에다가 보정계수 α를 곱한 것임.

근데 만약에 p(sushi | eat) 이 주어지지 않았다면 이 값을 구해야 함
그러면 p^*(sushi | eat) 을 구해야 하는데 이 값은

p^(sushi | eat) = alpha(eat) p(sushi) 로 구할 수 있음

요약

P(sushi | i eat) 없음
→ ⇒ backoff 필요

P(sushi | eat) 있음
→ ⇒ P_BO(sushi | i eat) = α(i eat) × P^*(sushi | eat)

그런데 P(sushi | eat)도 없음
→ ⇒ 다시 backoff 필요

그럼 어떻게 하냐?
→ ⇒ P^*(sushi | eat) = α(eat) × P(sushi)

결국 최종 식은 이렇게 됨
→ ⇒ P_BO(sushi | i eat) = α(i eat) × α(eat) × P(sushi)

Kneser-Ney Smoothing

katz 보다 더 잘 쓰이는.. (네이절 네이 스무딩)

bigram prob 를 구할 때의 식
bigram 에서 d 만큼 discount
unigram probability 의 일정량을 더해줌 (람다를 곱한 값)

katz와 뭐가 다르지?
- unigram prob 구하는 식이 좀 다름
york 가 mocha 보다 훨씬 많이 나오는 단어
- 그치만 이 문장 안에서는 mocha 가 나와야 함..
- 문맥에 따라서 나올 확률이 달라진다..
- bigram 으로 unigram 을 구할 때 문맥을 고려해서 구한다...
  - 그래서 단순하게 unigram 을 사용하면 안되니까...
  - context를 고려해줘야 한다는 의미
  → 이런 상황에서는 "mocha"가 새로운 문맥에 나올 가능성이 더 높다고 봐야 하는데, 기존 unigram 확률로는 이를 반영할 수 없음.

example

마찬가지로 training corpus 에 count 가 없어서 P(sushi | i eat) = 0 으로 되니 kneser - ney smoothing 을 해주는 상황.

p(sushi | eat), p(sushi) 모두 모르는 상태 -> 계산해줘야 함.
p_continuation 을 이용해서 구할 예정.

d = 0.1 (보통 0~1 사이의 값)
i eat pizza : 2번
i eat hamburger : 3번
eat sushi : 5번
sushi가 나오고 그 뒤에 뭐가 나오는 단어가 각각 얼마나 나온는지 구해서 possible bigram count = 0.4 라고 가정
observe값 가정하기.

-> 이외에는 정보가 없음

p(sushi| i eat)

max(count(i eat sushi) - 0.1, 0) = 0

-0.1 < 0 => 0

\lambda (i eat) = 0.1/5 * 2 = 0.04

i eat -> pizza, i eat -> hamburgers => 2 + 3 = 5

i eat과 관련된 3gram prob 를 모두 셈 각각 2번, 3번 을 더해서 5번

i eat 다음에 나오는 unique 한 word 종류가 pizza, hamburgers -> 2종류

그래서 람다를 구할때 discounting factor d 를 5번으로 나누고, 2종류를 곱해준 것...

p(sushi | i eat) 을 계산하려면

람다(i eat) * p(sushi | eat) 으로 구하는데

p(sushi | eat) 을 또 재귀적으로 계산해야함

람다(eat) 을 구해야하는데

여기서는 2 + 3 + 5 = 10번

eat 다음에 나오는 unique 한 word 종류는 eat, hamburgers, sushi -> 3종류

그러니까 0.1 을 10번으로 나누고 3번 곱해줌

주어진 p(sushi) = 0.4

그러면 최종 0.49 + 0.03*0.4

unigram?
- Regular count for the highest-order n-gram, or the number of unique single word contexts for lower-order n-grams
- 예: P(sushi)를 계산한다면, 기존 방식은 "sushi"가 얼마나 자주 나왔냐를 보지만,
- Kneser-Ney은 "sushi가 얼마나 다양한 앞 단어와 함께 나왔는가"를 본다.
recursion based case
- n-gram → (n-1)-gram → ... → unigram → uniform 분포
- unigram -> empty string
- 마지막에 → uniform 분포에 interpolation (공백 context 기준)
- 여기서 ε(빈 문자열)은 "어떤 문맥도 없음"을 의미함.
- 이때 uniform 분포 또는 전체 unigram 분포를 기반으로 마지막 보정