
Naive Bayes, Evaluating
Naive Bayes는 Language Model?

핵심 아이디어
Naive Bayes는 단어들의 등장 확률을 기반으로 문장의 클래스를 분류하는데, 이 과정이 마치 언어 모델처럼 작동한다는 점에서 클래스별 unigram language model로 해석할 수 있다.
-
Unigram 기반
Naive Bayes는 단어 하나하나를 독립된 feature로 보고 사용한다. 이건 곧 언어 모델에서의 unigram 방식과 같다. -
텍스트의 모든 단어 사용
특정 단어 subset만 고르지 않고, 문장 안의 모든 단어를 사용해 확률을 계산한다. -
클래스별로 따로 학습됨
Sarcastic과 Not Sarcastic처럼 각 클래스마다 따로 확률 분포를 학습한다.
→ 즉, 클래스 전용 언어 모델을 만든 것과 같다. -
단어뿐 아니라 문장 전체 확률도 계산 가능
단어들이 독립이라고 가정하면, 문장 전체의 확률은 단어 확률의 곱으로 표현할 수 있다.
수식
문장 S가 주어졌을 때, 클래스 ( c ) 에 대한 likelihood..
문장이 Sarcastic일 때 이 문장이 나올 확률은 얼마일까?
P(S | c): "클래스 c일 때, 문장 S가 등장할 확률"
문장 S의 전체 확률은 클래스 c일 때 각 단어가 등장할 확률을 전부 곱해서 계산..
이 수식은 결국 Naive Bayes의 핵심 가정인 독립성(naive assumption)을 바탕으로 한 것이다.
이후에 베이즈룰을 적용해서 P( c | S) 를 구함
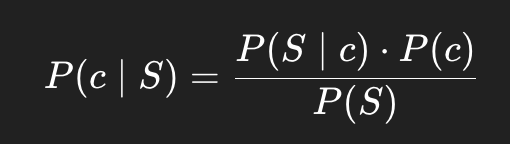
정리
Naive Bayes는 단어들의 확률을 통해 문장을 모델링하며, 클래스별 unigram 언어 모델처럼 동작한다. 단어들의 독립성을 가정하고, 문장 전체 확률도 계산할 수 있다.
Likelihood 계산
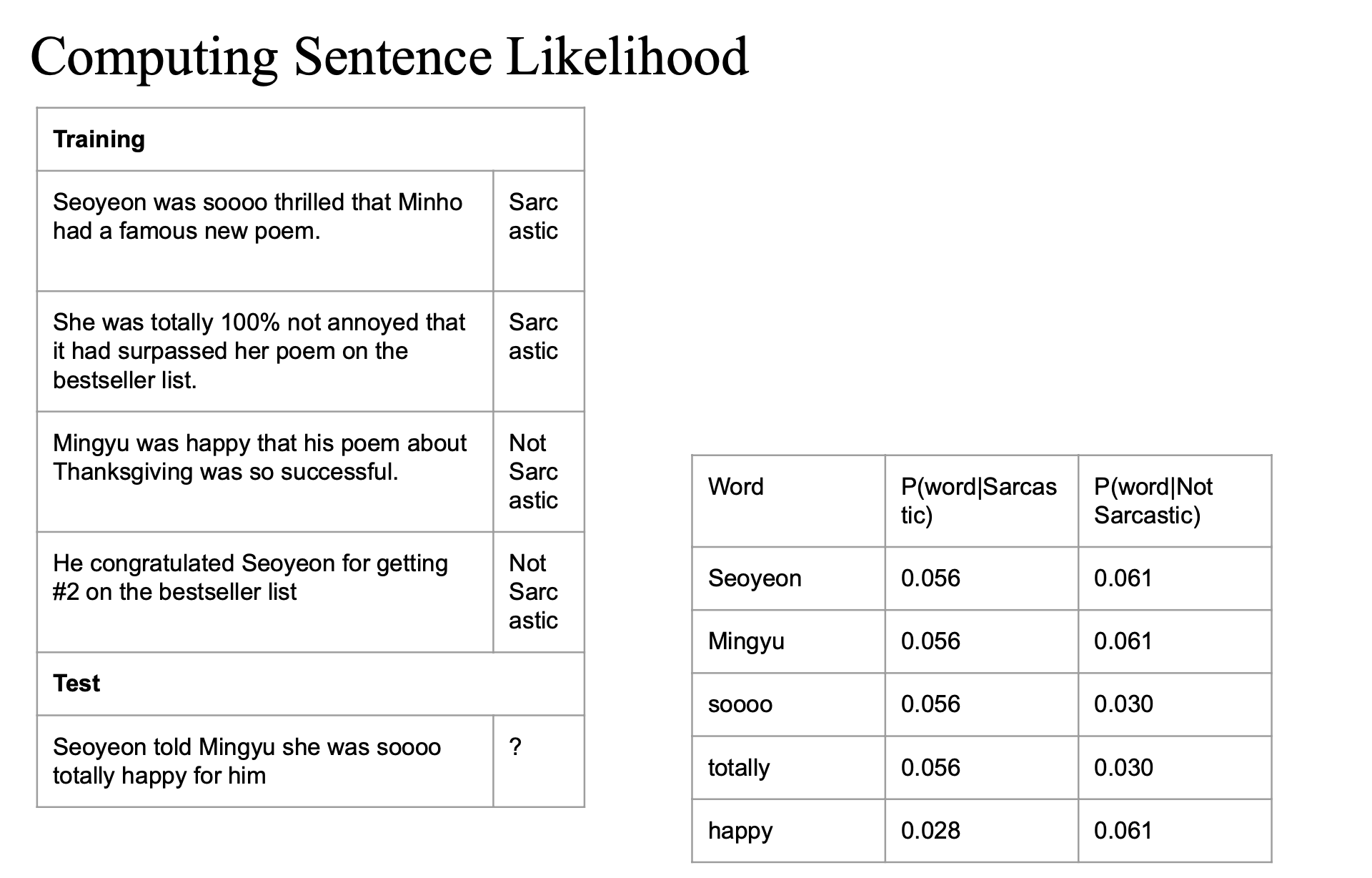
간단한 데이터셋으로 문장이 sarcastic한지 아닌지를 분류하는 과정..
DataSet
- 학습 데이터: Sarcastic/Not Sarcastic 레이블이 달린 문장들
- 테스트 문장:
"Seoyeon told Mingyu she was soooo totally happy for him"
이 문장이 sarcastic인지 아닌지를 Naive Bayes로 분류..
단어별 조건부 확률 구하기
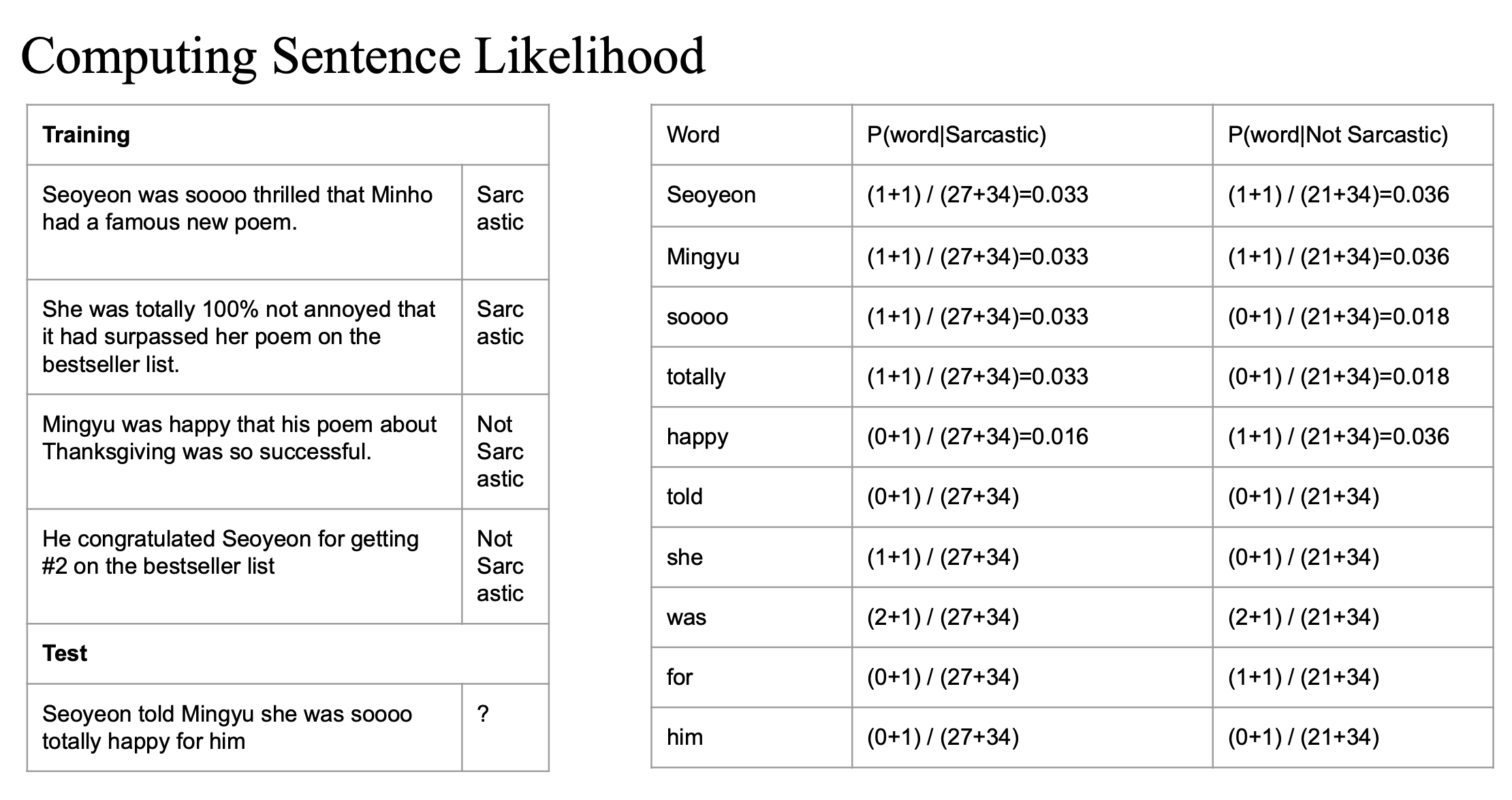
각 클래스에 대해 등장하는 단어 수를 세고, Laplace smoothing을 적용해 확률을 계산한다.
- (n + 1) 은 laplace smoothing
- n 은 해당 클래스에서 특정 word가 실제로 등장한 횟수
- 27은 sarcastic 클래스에 속한 문장들에서 등장한 단어의 총 개수
- 34는 전체 클래스에서 등장한 고유 단어(vocabulary)의 수
- unique words
이 과정을 테스트 문장에 등장하는 모든 단어에 대해 반복..
문장 전체가 나올 확률 (Likelihood) 계산
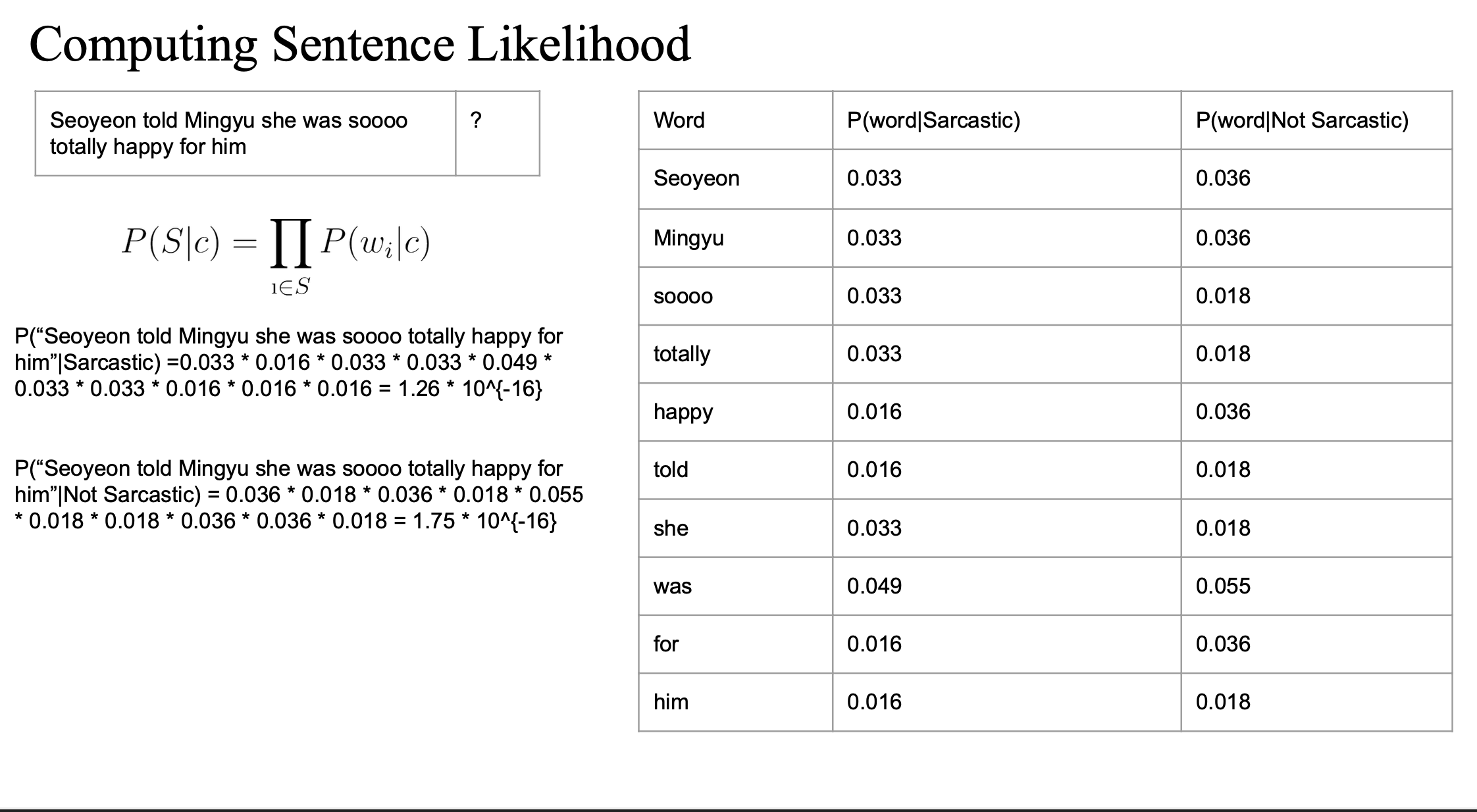
조건부 확률들을 모두 곱해 문장이 클래스 안에서 나올 확률을 계산
"Seoyeon told Mingyu she was soooo totally happy for him"
은 Not Sarcastic할 가능성이 더 높다..!
Gold Labels

실제 사람들이 직접 라벨링 하는 작업 -> 데이터셋 구축..
Contingency Tables
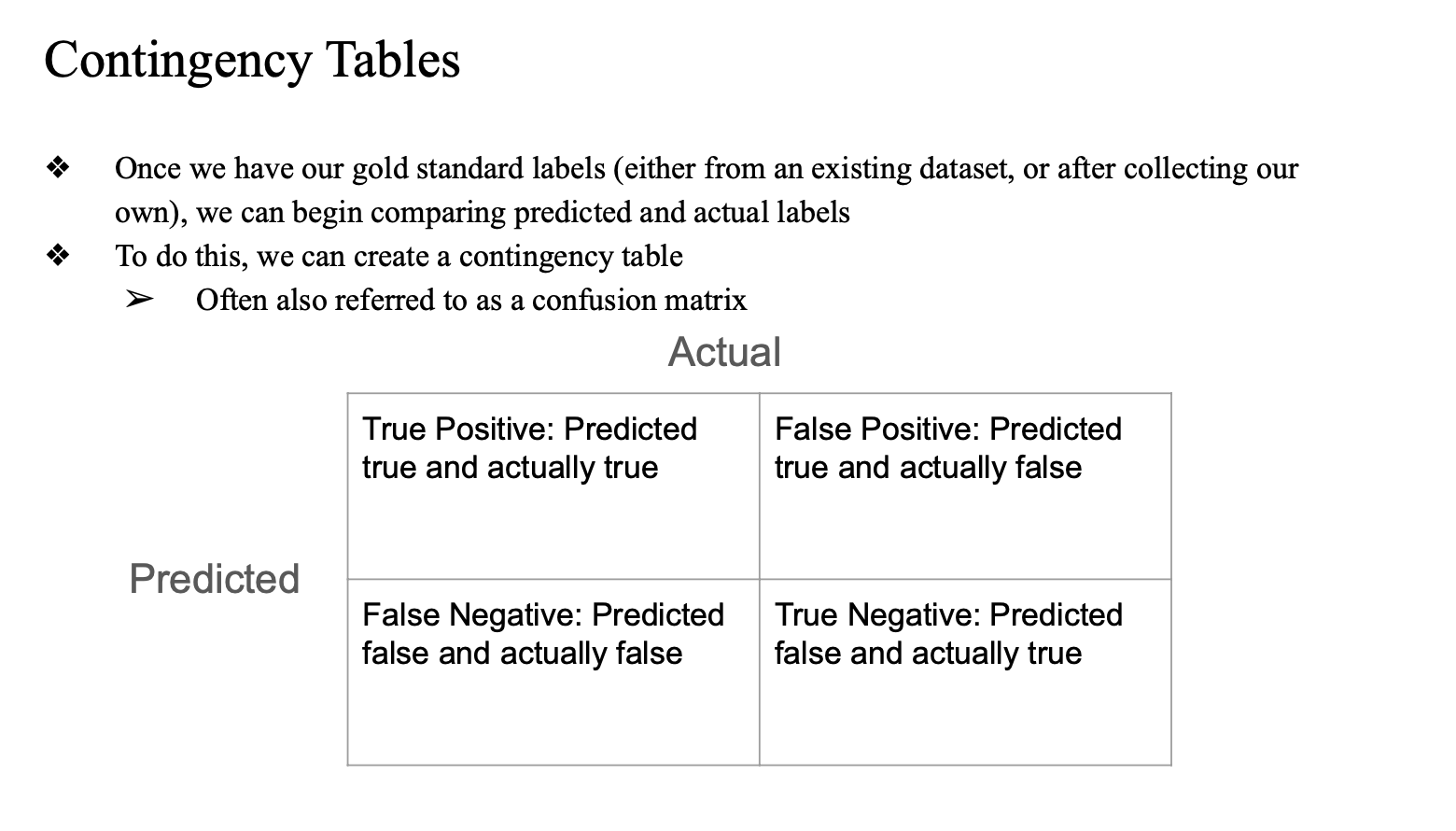

다양한 지표를 통해 모델 성능 평가..

accuracy 만으로 평가하면 생기는 문제...

Example
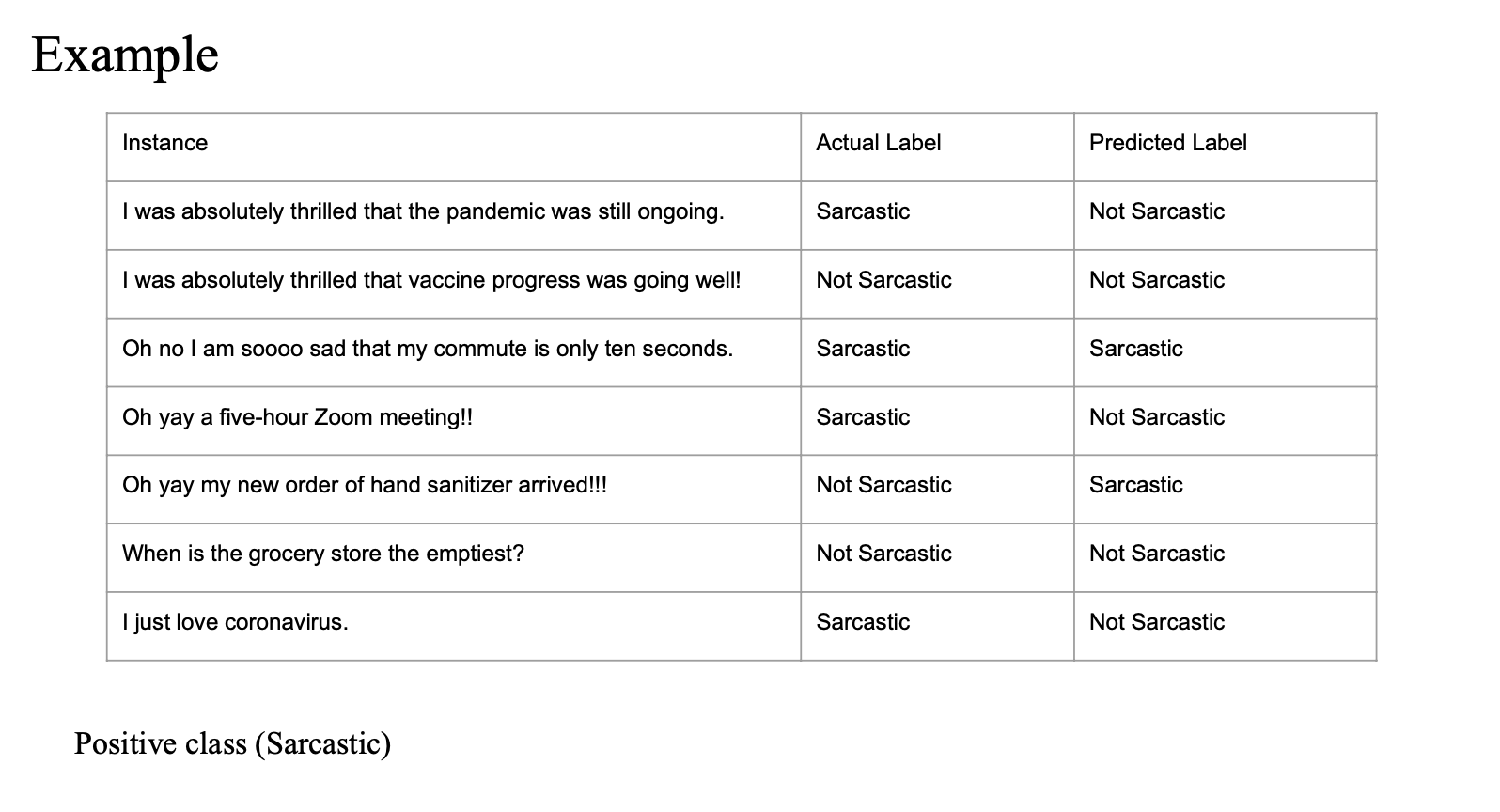
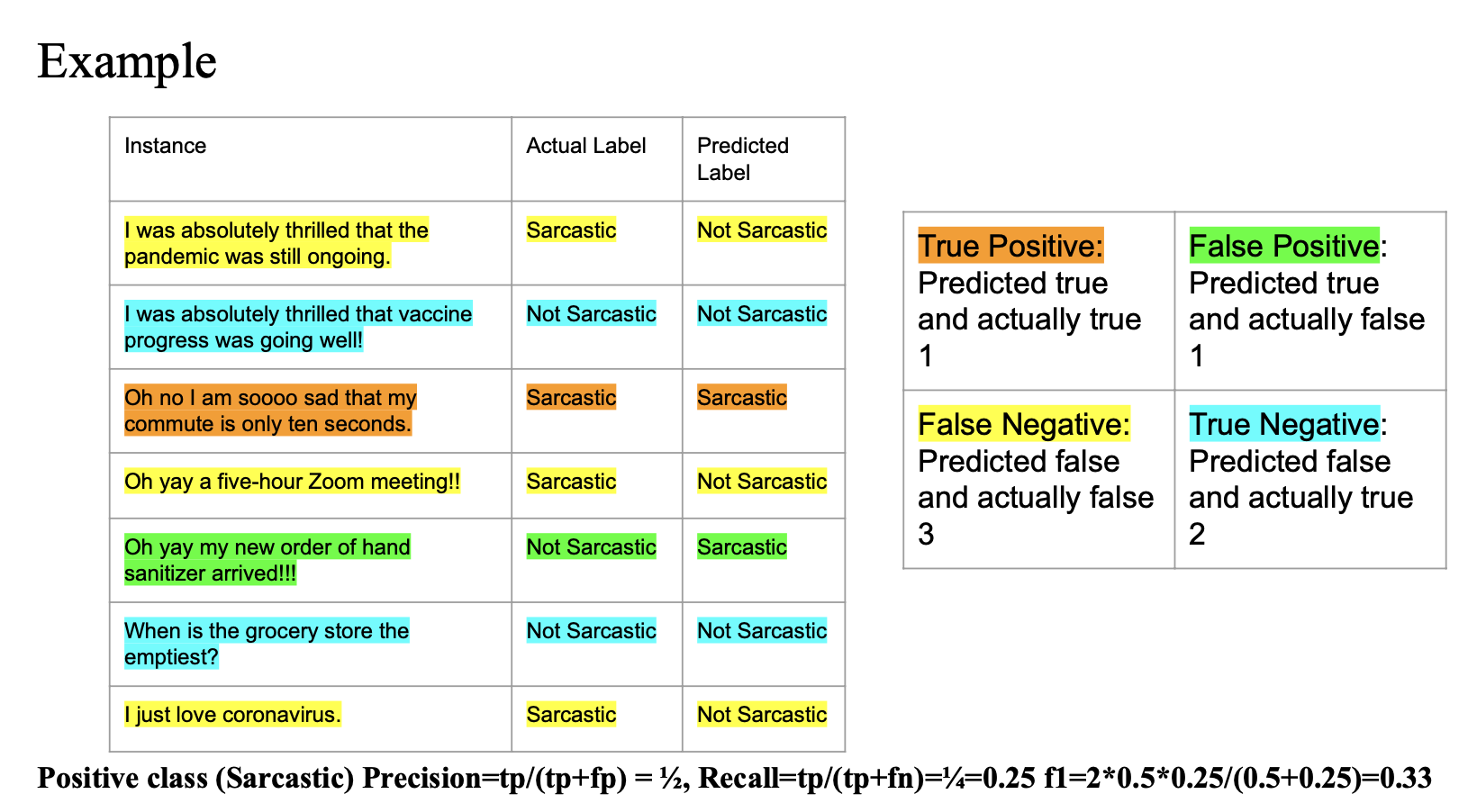
Precision
- Predicted label 에서 (class: Sarcastic) 인 경우 중에 Actual label 도 (class: Sarcastic) 인 경우
- 2개 중에 1개 = 1/2
Recall
- Actual label 에서 (class: Sarcastic) 인 경우 중에 Predicted label 도 (class: Sarcastic) 인 경우
- 4개 중에 1개 = 1/4
f1 score
- 2 * P * R / (P + R)
2개 이상 클래스?

- 대부분의 NLP 분류 과제는 2개 이상의 클래스..
- 감정 분석 →
positive,negative,neutral - 품사 태깅 →
noun,verb,adjective, ... - 감정 인식 →
happy,sad,angry, ...
- 감정 분석 →
- 그래서 우리는 multi-label classification 또는 multinomial classification이 필요함.
Multi-Label Classification

- 하나의 문서가 여러 개의 라벨을 가질 수 있음
- 방법:
- 각 클래스마다 이진 분류기 하나씩 따로 만들기
positive vs. not-positive,negative vs. not-negative, ...
- 테스트 문서에 대해 각 분류기 돌리기
- 각 분류기가 독립적으로 예측해서 여러 라벨 부여 가능
- 각 클래스마다 이진 분류기 하나씩 따로 만들기
Multinomial Classification

- 문서당 하나의 라벨만 부여됨
- 세팅은 multi-label과 똑같음:
- 각 클래스에 대해 이진 분류기 만들고, 테스트 문서에 대해 각 분류기 돌림
- 차이점은 예측 방식:
- 각 분류기의 점수 중 가장 높은 하나만 선택
Multi-Class Contingency Matrix
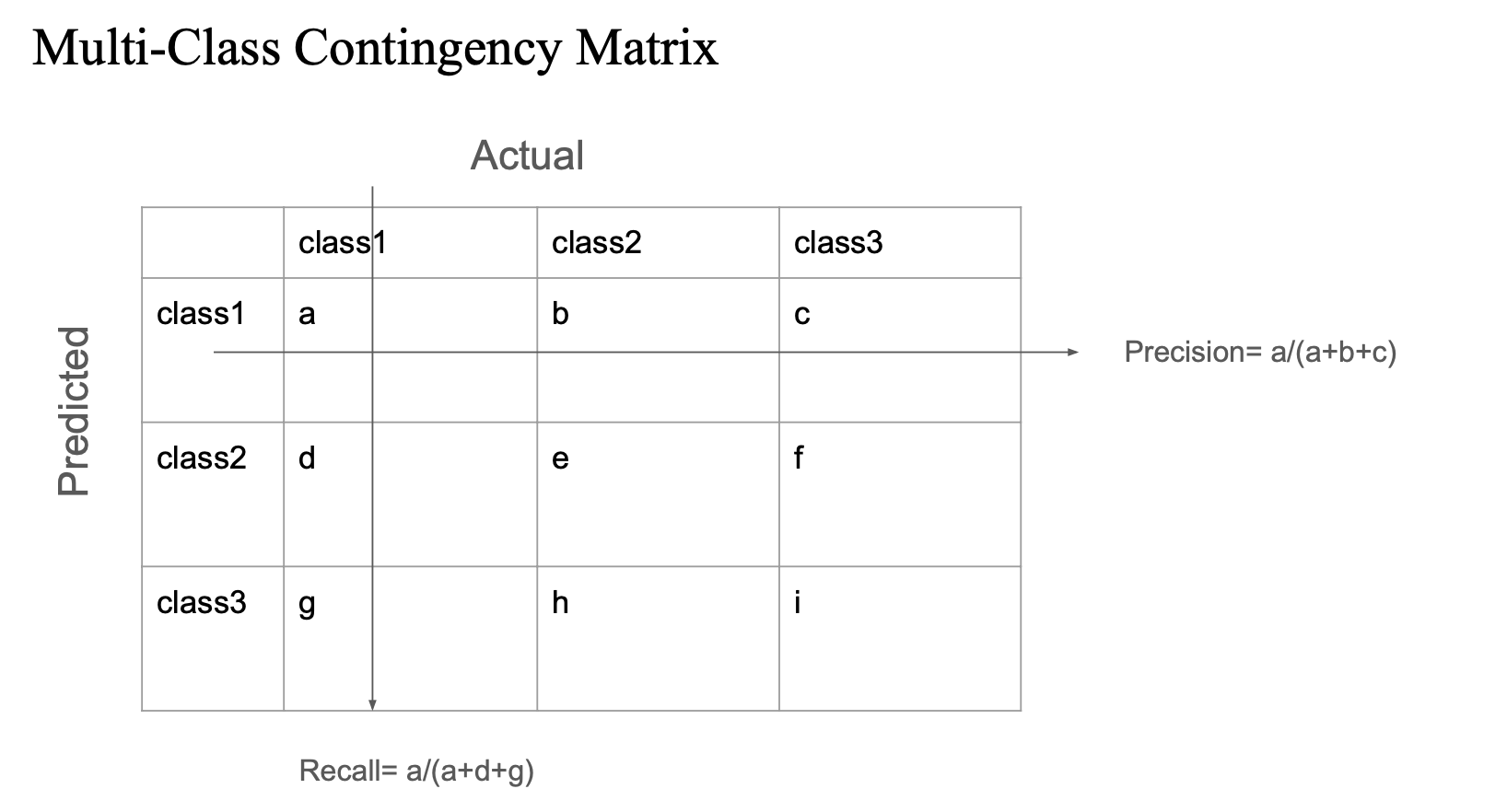
- 다중 클래스에서 모델의 성능을 평가할 때 사용하는 혼동 행렬 (Confusion Matrix)
- 행: 모델이 예측한 라벨
- 열: 실제 정답 라벨
a는 class1으로 예측했고 실제도 class1인 경우 → True Positiveb,c는 잘못 예측한 경우
- Precision (정밀도): 예측한 것 중 맞춘 비율
→a / (a + b + c) - Recall (재현율): 실제 정답 중 맞춘 비율
→a / (a + d + g)
Macroaveraging, Microaveraging

- 목적: 여러 클래스를 다룰 때 전체 시스템 성능을 요약하려는 방법
- Macroaveraging:
- 각 클래스별로 precision, recall 등을 계산한 뒤 평균
- → 각 클래스가 동일한 중요도를 가짐 (데이터 수가 적어도 동일 비중)
- Microaveraging:
- 모든 예측을 하나의 큰 confusion matrix로 통합해서 계산
- → 클래스 간 불균형이 있을 때 더 현실적인 평가 가능
Macroaveraging
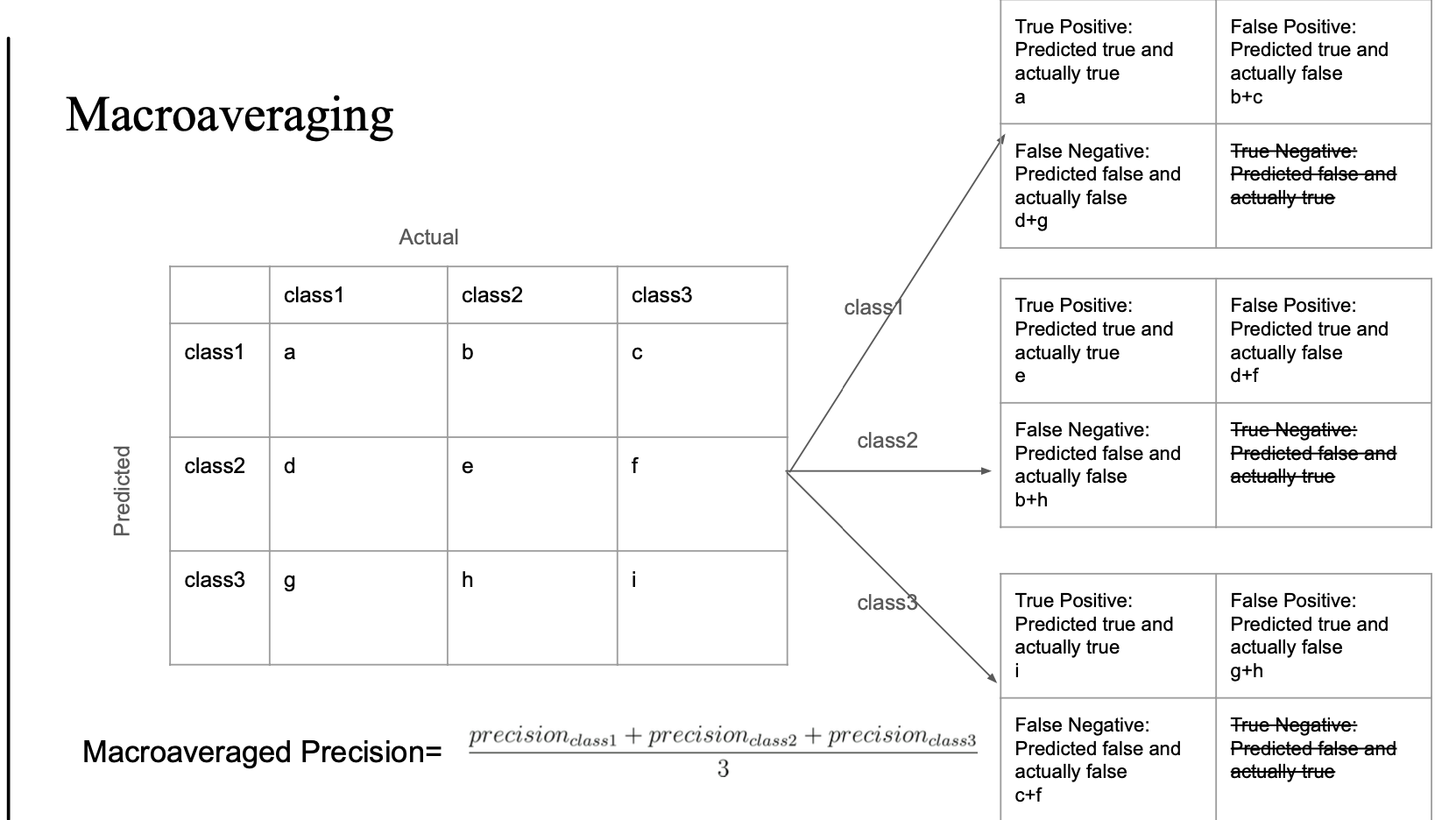
- confusion matrix를 통해 각 클래스마다:
- True Positive (TP), False Positive (FP), False Negative (FN) 계산
- 그리고 각 클래스에 대해:
- precision = TP / (TP + FP)
- recall = TP / (TP + FN)
- 마지막으로:
Macro Precision = (precision_class1 + precision_class2 + precision_class3) / 3
Microaveraging
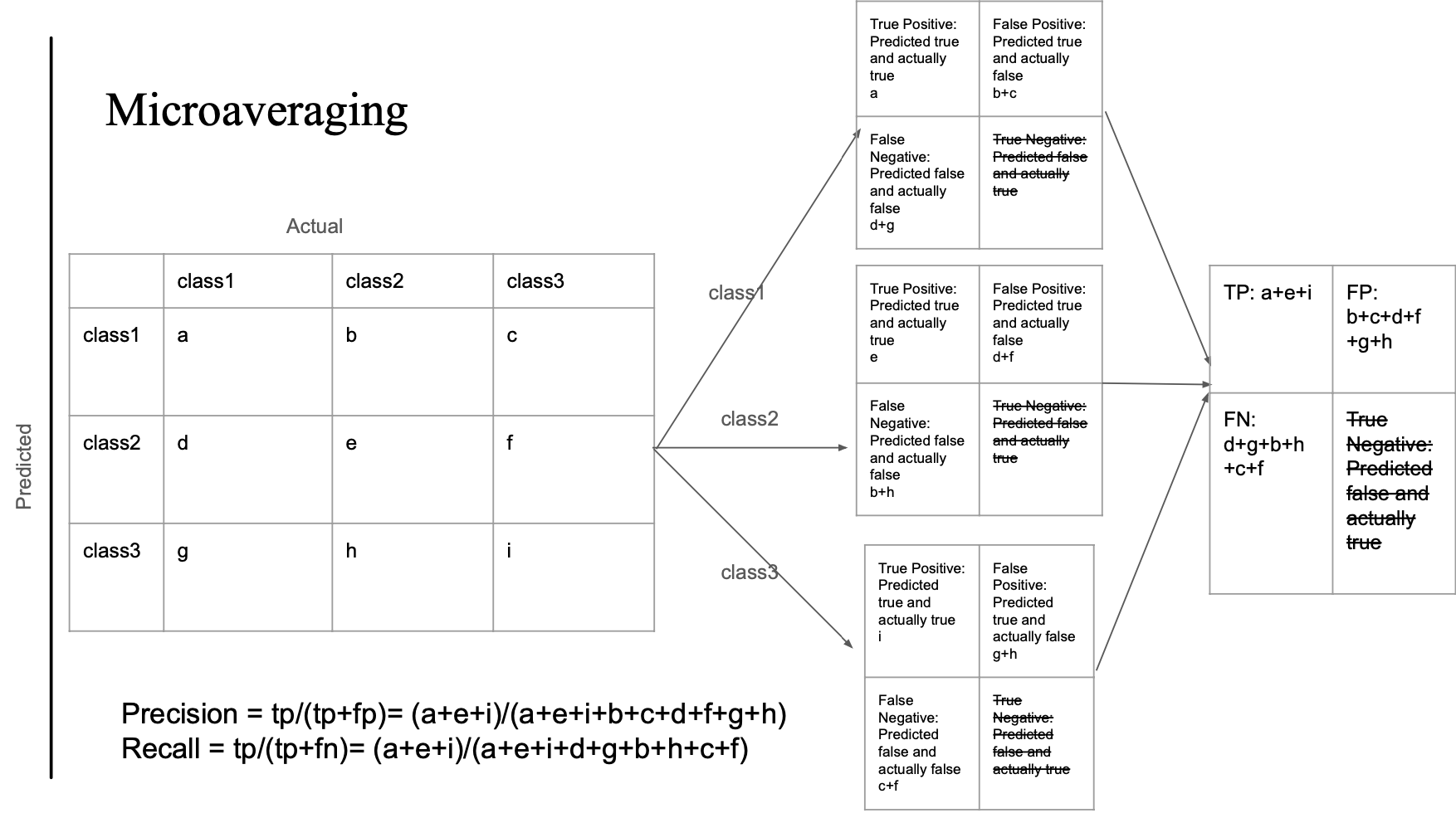
- 모든 TP, FP, FN을 합쳐서 계산함
- 예시 기준으로:
Precision = (a + e + i) / (a + e + i + b + c + d + f + g + h) Recall = (a + e + i) / (a + e + i + d + g + b + h + c + f) - 이 방식은 모든 예측이 동일한 단위로 평가됨 → 데이터 수 많은 클래스가 영향 더 큼
- Macroaveraging:
- 각 클래스의 성능을 개별적으로 계산해 단순 평균 → 클래스마다 동일한 비중.
- Microaveraging
- 전체 예측을 통합해 계산 → 데이터가 많은 클래스가 더 큰 영향.
