
ch08 Logistic Regression and Conditional Random Fields
Text classification

- input 어떻게 표현?
- vectorization
- Bag of Words, TF-IDF, Word Embedding 등
- classification function
- 예측된 클래스 y hat 을 계산
- sigmoid, softmax
- objective, loss function
- 예측값과 실제값 차이 게산
- Optimization function
- 하이퍼파라미터 튜닝..
- gradient descent..
logistic regression classifier

가중치 w 와 바이어스 b -> sgd, cross-entropy loss
-> sigmoid 함수 -> p(y|x)가 높은 레이블
Binary Logistic Regression

-
새로운 입력 x가 클래스 a인지 b인지 판단하는 분류기
-
최적의 값을 찾는것이 목표
-
weight 와 bias 를 계속 업데이트
-
이 값은 true 값과 predict 값의 차이 (loss) 를 최소화 하는값
-
각 feature 당 하나의 weight 가 있음
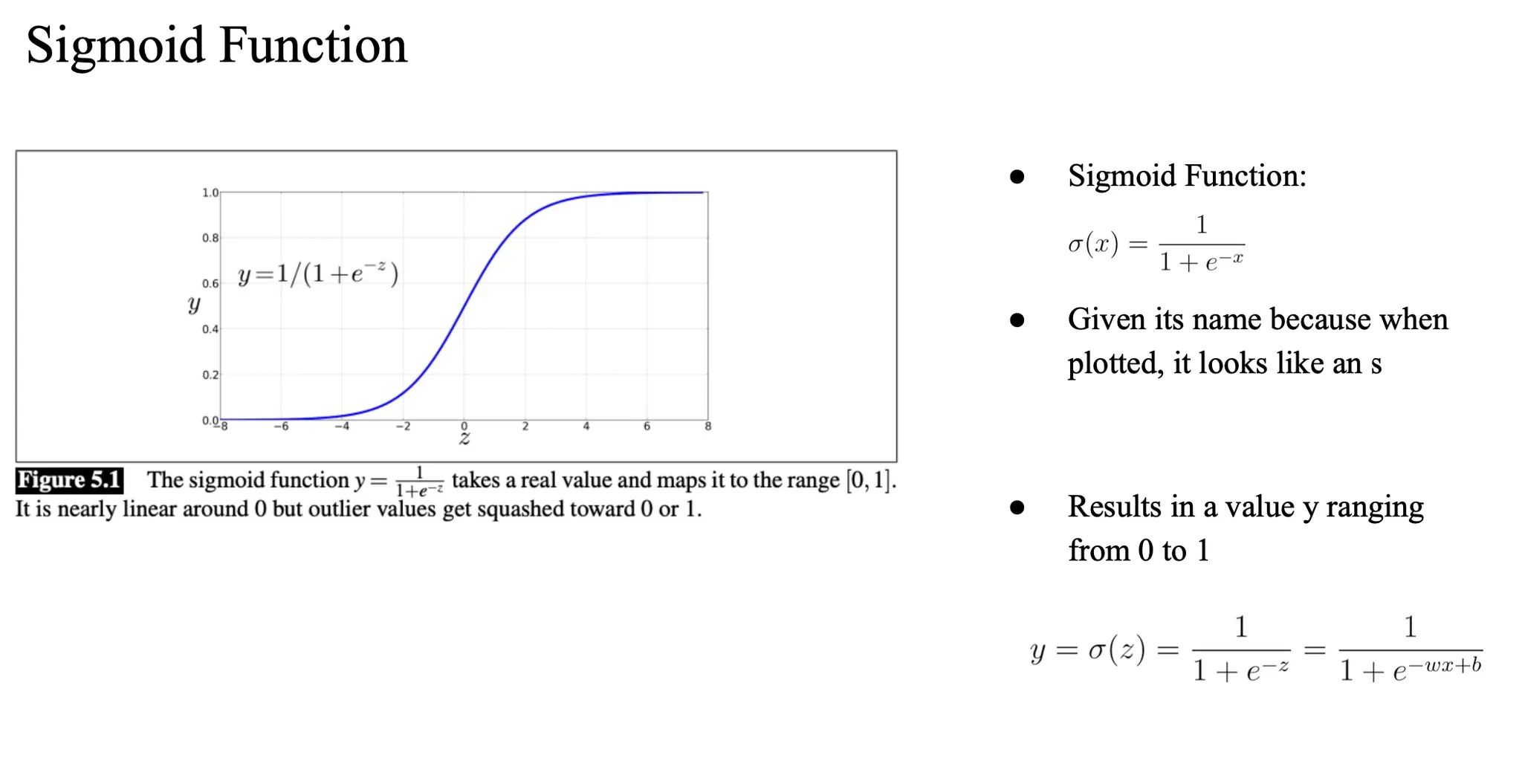
Sigmoid Function

z를 W * X + b 라고 하면 이건 선형함수 결과..
우리는 확률이 필요하므로
-> 시그모이드 함수에 통과시켜서 확률(0~1 값)로 변환함
decision boundary
decision boundary (0.5) 기준으로 클래스 분류
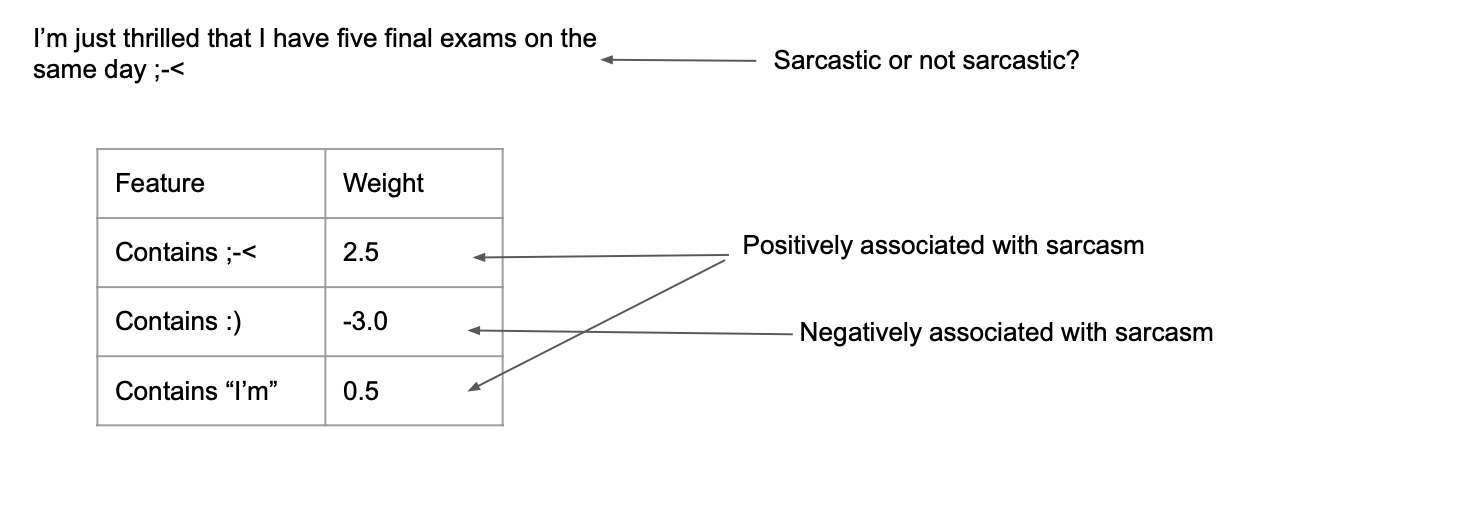
Example


- 이모지(;)가 있는지 없는지에 따라서 weight 를 구성함
- 원래는 벡터값에 대해서 weight 를 설정해줌
- 주어진 문장에 대해서 feature vector representation 을 나타냄
- 1과 0 으로 있는지 없는지 구분해줌
→ 이 값을 bias로 설정
- 1과 0 으로 있는지 없는지 구분해줌
Loss Function
Cross-entropy loss
예측된 확률 분포와 실제 정답 분포(One-hot)를 비교하는 방식
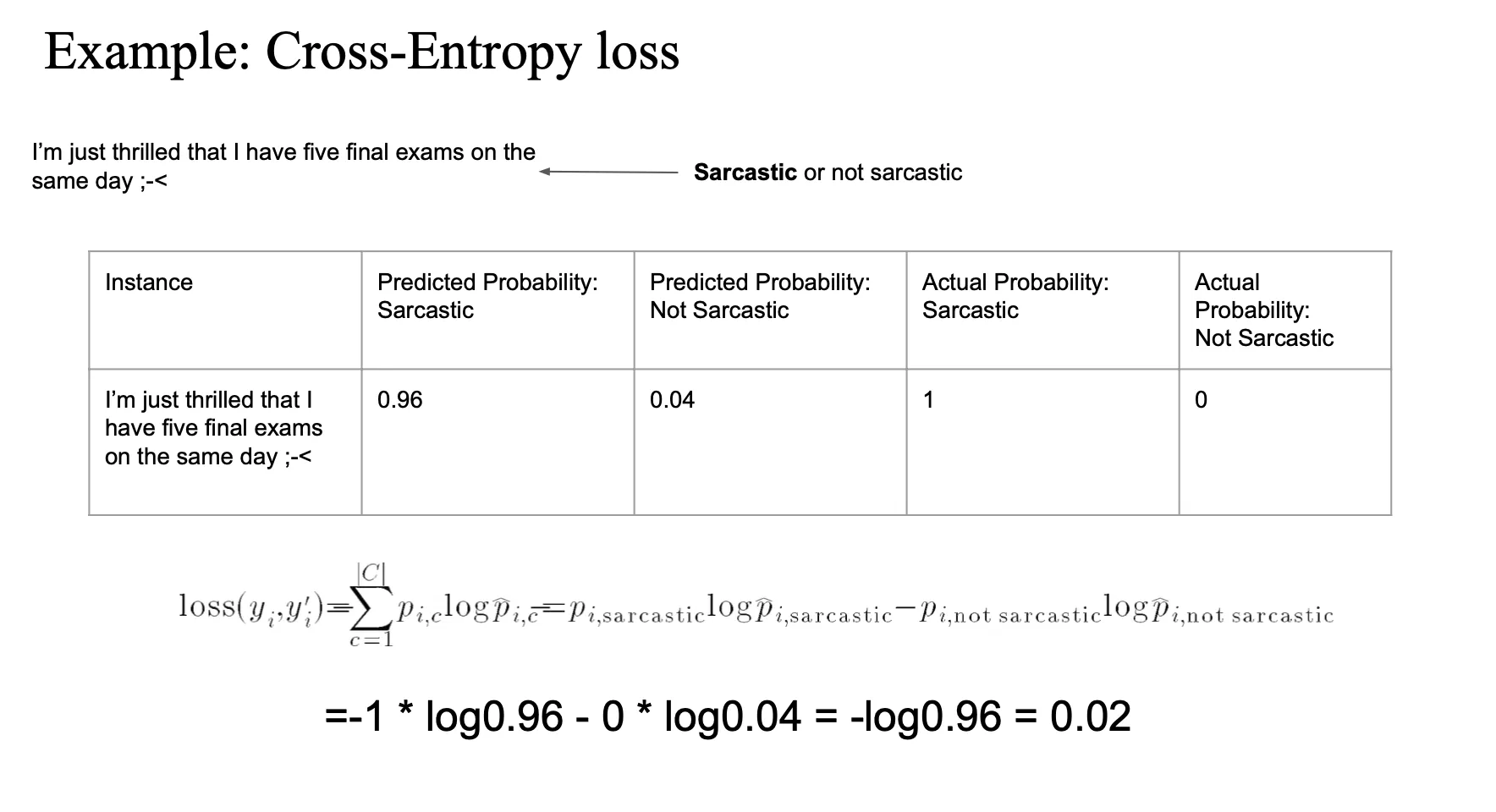
- we do this using a conditional maximum likelihood estimation
- 결국 어떤 정답 label 에 대한 probability 를 높이고 싶은 것이 목표..

true 일 때 1 값 → one hot
- cross entropy loss
- 1 과 예측값(0.96) 의 차이를 계산
- 0과 예측값(0.04) 의 차이 계산
모든 클래스에 대해서 likelihood 를 계산 → cross entropy
true 클래스에 대해서만 계산 → Log liklihood loss
따라서 1,0 으로 분류할때 false 클래스의 Likelihood 는 0이 되어서 결국에 두 방법론이 같은 값이 나오게 됨
- negative log likelihood vs cross-entropy loss
- 언제 같은가? true label 에 대한 represent 를 one-hot 으로 가져갈때 같음
너무 1인 true 값만 과하게 학습 ?
→ model smoothing
→ model 칼리브레이션
Finding Optimal Weights
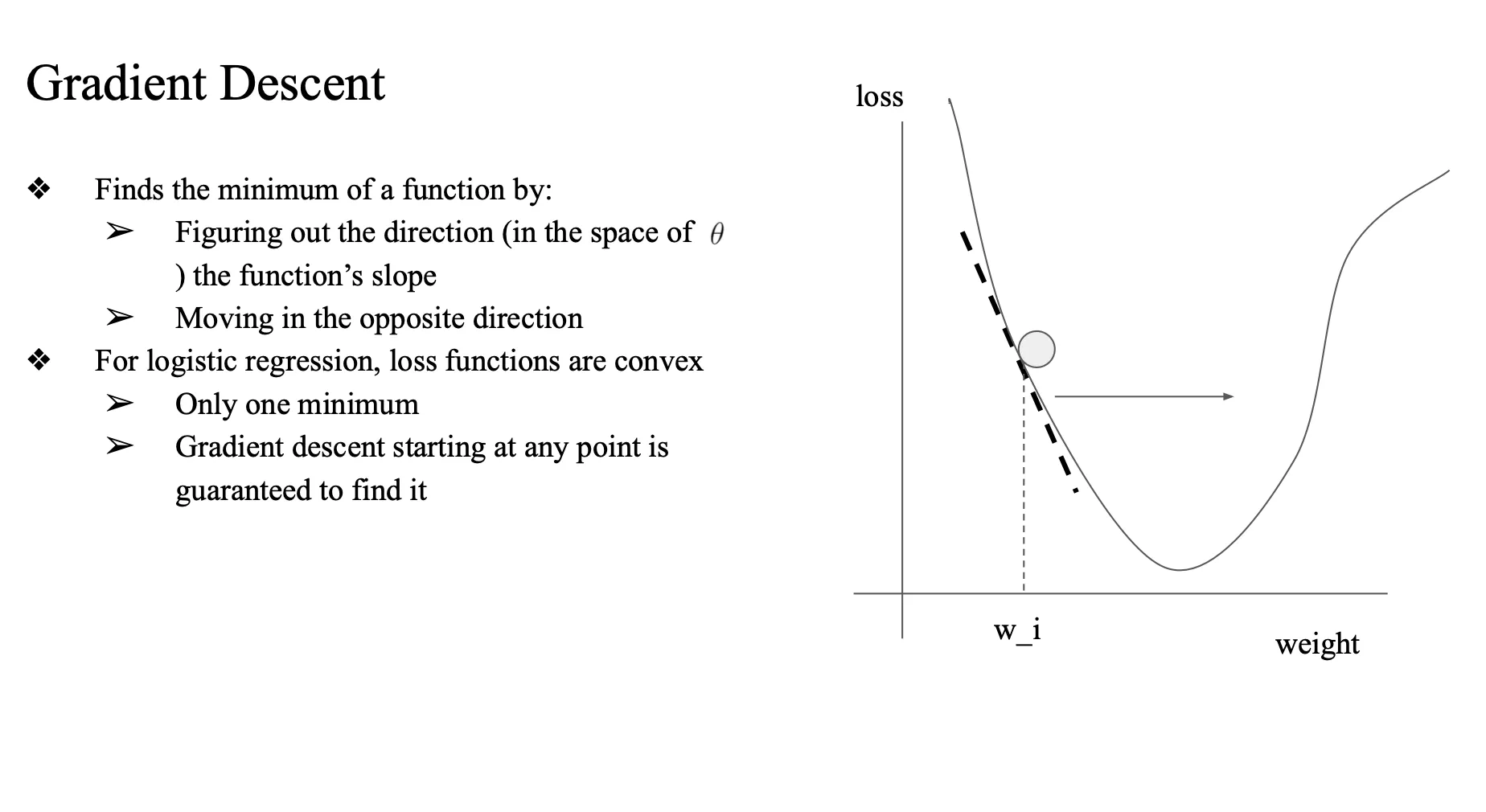
gradient descent 를 통해서 계산
Gradient Descent

- gradient 를 가지고 weight 업데이트
- loss의 gradient..
- 함수에서 기울기 값이 gradient
- 기울기의 반대 방향으로 업데이트
- 마이너스라면 플러스 방향으로 w를 업데이트
- w가 증가하는 방향 → 공이 밑으로 내려와야.. → w_i 가 오른쪽으로 이동
- 이동할때 도대체 얼마만큼의 step size?
- learning rate (lr)
- convex → only one minimum
- convex하다 → 글로벌 미니멈이 로컬 미니멈 → 어디에서 시작하든 → 결국 minimum 에 도달
수식

- 기울기의 반대방향으로 파라미터 이동..
- 세타가 현재 가중치 벡터
- theta(t+1) = theta(t) - (학습률)*현재 손실에 대한 기울기
- 이런식으로 업데이트
이 걸 자동으로 게산 → Pytorch
cross entropy loss 까지 구현
→ pytorch , loss.backword 이용해서 자동으로 w,b 업데이트 해줌

미분하면 prediction 에서 정답값을 배고 input x 를 곱해준 형태가 됨
example

초기에는 weight 가 0
bias, 학습률 각각 0, 0.1로 가정...
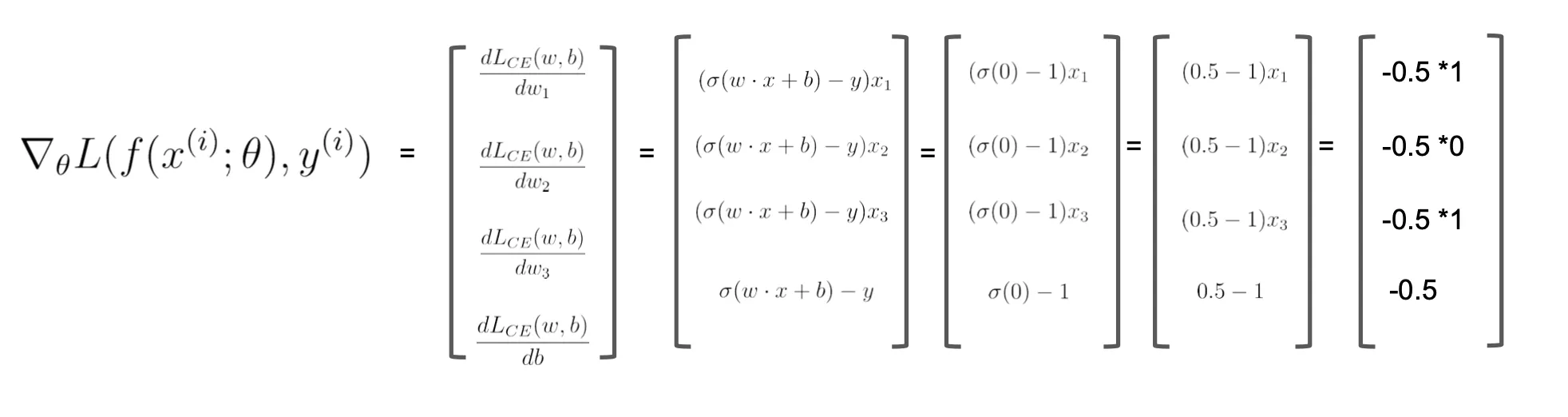
-
시그모이드 계산
- z = w*x+b
- 시그모이드(z) 대입
- 여기서 z를 구할때의 x값은 벡터값임
- 그래서 weight * value 값의 합임
- 0*1 + 0*0 + 0*1 = 0
- 그래서 sigma(0)
- 그래서 weight * value 값의 합임
-
그래디언트 계산
- (y` - y) * x_i
- (0.5 - 1)*x_1 ...
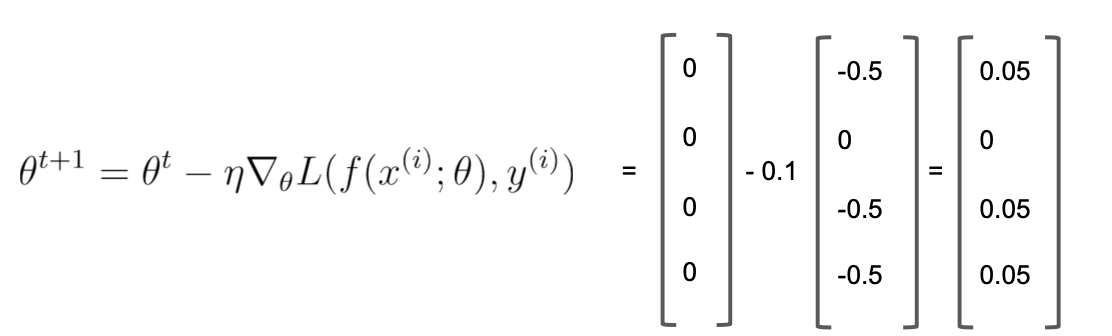
- 가중치 업데이트
- theta(t+1) 업데이트
example 2

weight 값과 value값이 변경됐는데 계산과정 참고하기
