Markov Decision Processes (MDP) - 2

Lily·2023년 9월 13일

Markov Decision Process reinforcement learning

Markov Deicision Processes에서 중요한 4가지 토픽은 다음과 같으며,
지난 시간에 이어 이번 시간에는 3) Markov Decision Processes
4) Extensions to MDPs를 다뤄보도록 하겠다.

1) Markov Processes
2) Markov Reward Processes
3) Markov Decision Processes
4) Extensions to MDPs

이전 포스팅은 Markov Decision Processes - 1 에서 확인이 가능하다.

Recap을 위해 MDP의 구성요소를 다시 확인해본다면 다음과 같다.

Definition

Agent:

앞으로 실험 상황에서 연속된 행동을 하게 될 주체, 대리인
State( $s_{t}$ ):

t 시간에서의 Agent의 상황과 상태
Action( $a_{t}$ ):

State $s_{t}$ 에서 Agent가 취할 수 있는 행동들
Reward( $R$ ):

Agent가 움직이면서(= Action $a_{t}$ 를 진행하면서) 발생하는 보상 점수
Transition probability(=matrix)( $P_{ss'}$ ):

Agent가 $s_{t}$ 에서 특정 다음 상태인 $s_{t+1}$ 로 넘어갈 확률을 모아놓은 분포
$P_{ss'} = P[s_{t+1}=s'|s_{t}=s]$ 로 풀어쓸 수 있다.
Discount factor( $\gamma$ ):

Agent가 최단, 최소 경로로 인한 합리적인 보상을 얻게 하기 위하여, 시간에 제약을 두기 위한 factor.
오랜 기간에 걸쳐 목표달성을 하는 것에 대한 패널티를 줌 [ $0 \le \gamma \le 1$ ]

Markov Decision Processes

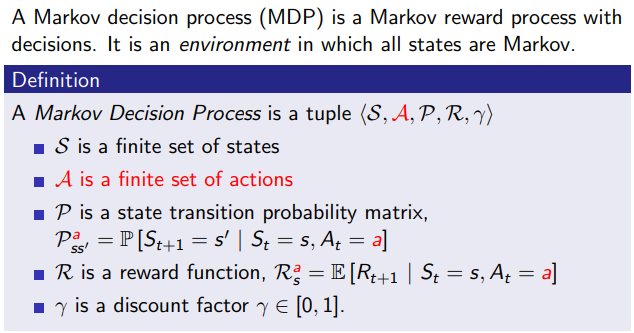
Markov Decision Process(MDP)는 기존 Markov Reward Process(MRP)에 action이라는 결정을 추가한 것을 의미한다. 이는 현재 상태에서 다음 상태로 넘어갈 때, 이전(MRP)과 다르게 action이라는 개념을 반드시 취해야 하고, 이 action에 따라 받는 보상과 상태가 달라지면서 어떤 action을 취했느냐에 따라 최종 optimal value를 결정하게 되면서 중요한 개념이 되었다고 할 수 있다.

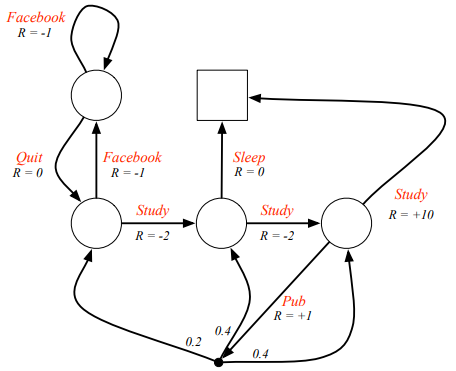
두 그래프에서 위의 그림이 MRP, 아래 그림이 MDP를 의미하는데, 빨간색 표시를 보면 각각이 어디에 초점을 두는지 확인할 수 있다. 둘의 직접적 차이를 비교하면, MRP의 경우는 state가 정확하게 명시되어 있고 한 $s_{t}$ 에서 다음 $s_{t+1}$ 로 이동하도록 집중된 반면, MDP의 경우는 action이 다음 state를 결정한다. 다음 state에 대한 정보가 없는 셈이다. 그래서 action을 선택하는 것이 중요한 일이 되어버렸는데, 이를 잘 선택하기 위한 방식을 policy $\pi$ 라고 한다.

그래서 이제는 state sequence, state and reward sequence 를 설명할 때도, policy $\pi$ 를 껴넣고, action의 의미를 부각시켜 식을 전개하는 행태로 변하게 된다.

당연히 기존 MRP에서 가치를 측정하던 척도인 state value function $v(s)$ 도 $\pi$ 를 도입하면서, 조금 다른 형태가 되었고, $\pi$ 의 짝꿍인 action이 개입하게 되면서 위와 같이 state-value function $v_{\pi}(s)$ 와 action-value function $q_{\pi}(s)$ 가 새로 정의되었다. 사실 둘은 서로를 이용하는 관계이다. $v_{\pi}(s)$ 계산을 위해 $q_{\pi}(s)$ 를 이용하고, $q_{\pi}(s)$ 의 계산을 위해 $v_{\pi}(s')$ 을 이용하는, recursive 한 관계를 가지고 있는데 다음 그림을 통해 알아보자.

Bellman Expectation Equation

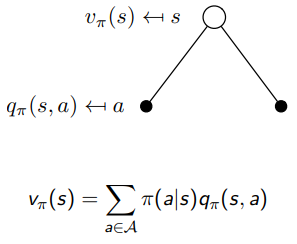
지난 포스팅과 같이, $v_{\pi}(s)$ 또한 Root node에서 한스텝 씩 가지를 뻗어나가고 연산하다가, 이를 추스리면서 결과값을 완성하는데, 한 가지 다른점은 중간에 action $a$ 를 선택하는 행동을 한다는 것이다(policy $\pi(a|s)$ ). 그리고 나서 디테일한 계산은 선택된 action $a$ 를 기준으로 $q_{\pi}(s,a)$ 에서 진행한다.

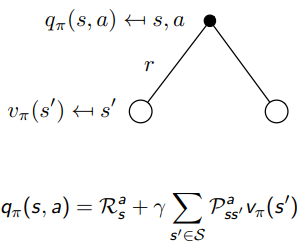
Action $a$ 가 결정된 후인 $q_{\pi}(s,a)$ 에서 비로소 이전 MRP에서 우리가 봤던 Bellman Equation

state value function $v(s)$ 를 두가지로 쪼갤 수 있는데, 매 순간마다
1) 다음 스텝에서의 reward $R_{t+1}$ 와
2) 그 후에 감가상각 되는 state를 $\gamma v(S_{t+1})$ 로 나타낼 수 있다.

를 적용하여, 조건 $a$ 를 덧붙인 위와 같은 식 $q_{\pi}(s,a)$ 를 도출하게 된다.

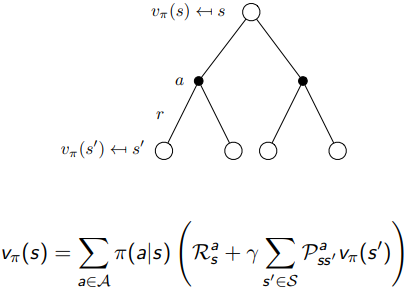
앞선 위의 두 트리를 이어붙이면, 다음과 같이 $v_{\pi}(s)$ 를 정리할 수 있다. $v_{\pi}(s)$ 는 action $a$ 를 먼저 선택 한 뒤, 그로부터 다음 state $s'$ 로 가는 동안의 리워드와 그 후의 시뮬레이션 값들을 합해나가는 과정이다.

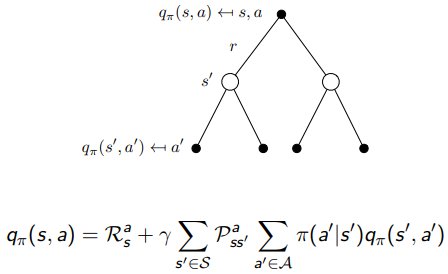
$q_{\pi}(s,a)$ 의 관점에서 보면, 마지막 $v_{\pi}(s')$ 를 $\pi(a'|s')q_{\pi}(s',a')$ 로 치환해서 다음 행동에 대한 action value function를 확인하는 과정이 될 수 있다.

이렇게 state-value function $v_{\pi}(s)$ 와 action-value function $q_{\pi}(s,a)$ 는 서로 맞물리며 연산되게 되어있다.

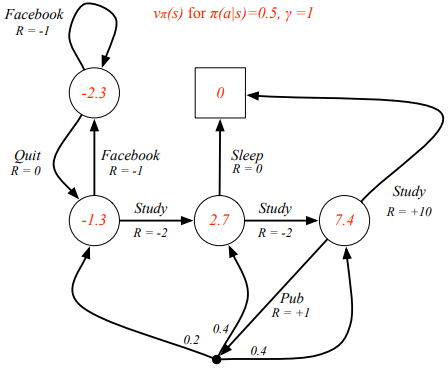
위의 그림은, policy $\pi(a|s)=0.5$ , $\gamma=1$ 일 때의 $v_{\pi}(s)$ 를 계산한 결과이다. (계산은 미리 Bellman Expectation Equation을 모두 연산해서 나온것으로 추정됨.)

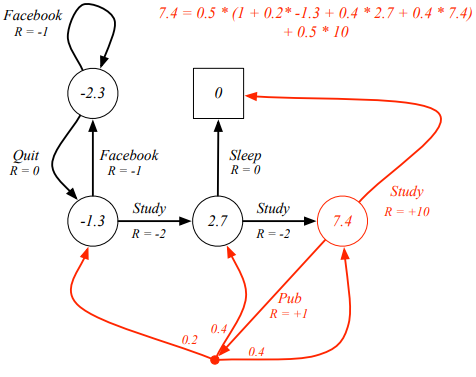
이 때, 빨간색으로 표시된 $v_{\pi}(s)=7.4$ 의 도출 과정을 보면, $\pi(a|s)=0.5$ 에서,
$7.4=v_{\pi}(s)=\sum_{a\in A} \pi(a|s)\bigg(R^a_{s}+\gamma\sum_{s'\in S}P^a_{ss'}v_{\pi}(s')\bigg)$ 와 같다는 것을 확인할 수 있다.

Bellman Expectation Eqation은 MRP에서와 유사하게 direct solution 형식으로 계산이 가능하다.

Optimal Value Function

우리의 궁극적인 목적은, MDP에서 가장 좋은 결과를 내는 optimal policy $\pi$ 를 찾는 것이고, 이는 각 state $s$ 에서 action $a$ 를 잘 선택하는 것과 연관이 있다. MDP는 1) 특정 state $s$ 에서 action $a$ 를 고른 후, 2) $a$ 로 인한 그 다음 시뮬레이션 결과를 구하는 구조로 되어있다. 따라서 $v_{*}(s)$ 와 $q_{*}(s,a)$ 는 서로 연관이 되어있다. 우선은 optimal value를 구하기 위해서 각 state에서 값이 max가 되는 policy $\pi$ 를 찾는 것이라 생각하고, 자세한 내용은 뒤에서 알아보도록 하겠다.

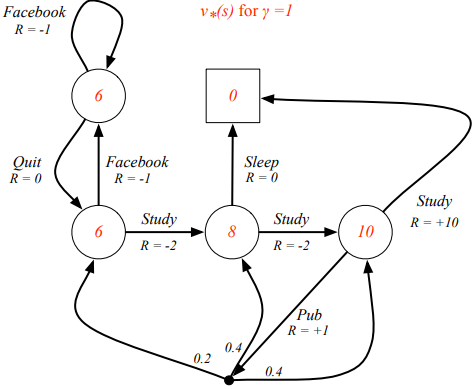
위의 그림은 Optimal state-value function $v_{*}(s)$ 를 나타내는 것으로, definition에 나타난 대로 생각해보면, 다음과 같이 이해할 수 있다. 먼저, 8이라는 숫자가 위치한 상태를 가정하고, 그 상태를 T라고 한다면, T에서 선택할 수 있는 다음 액션은 {Sleep, Study}이고, Optiaml 한 값은 $v_{*}(s)$ 의 정의에 따라 아래 두가지 케이스 중 최대값, 즉, $max((1), (2))$ 가 될 것이다.

(1) action {Sleep} $\approx$ $R+v_{\pi}(s')=0+0=0$
(2) action {Study} $\approx$ $R+v_{\pi}(s')=-2+10=8$

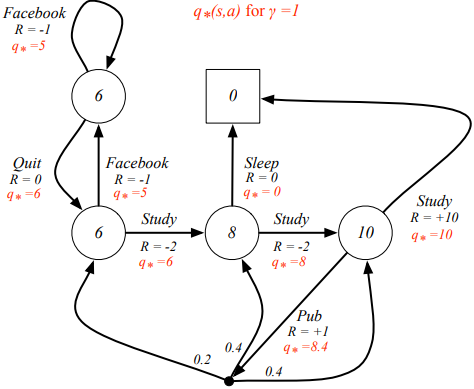
이 그림은 Optimal action-value function으로, $q_{*}(s,a)$ 의 관점에서 표시된 것이다.

Optimal policy $\pi_{*}$ 는 다른 모든 $\pi$ 에 대해 어떤 state $s$ 에서든지 간에 value $v_{\pi}(s)$ 를 구했을 때, 항상 값이 높아야 하고, optimal state/action value function 과 값이 같아야 한다. optimal policy $\pi_{*}$ 가 유일하지는 않고, 여러개 존재 할 수 있다고 한다.

Bellman Optimality Equation

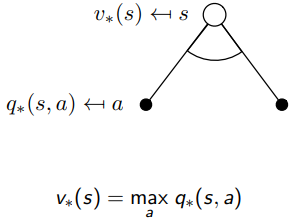
Bellman optimality equation의 $v_{*}(s)$ 는 이전 Bellman expectation equation의 $v_{\pi}(s)$ 와 개념 차이가 있고, $q_{*}(s,a)$ 와 $q_{\pi}(s,a)$ 는 같은 식이라고 볼 수 있다.

$v_{\pi}(s)$ 가 위 그림에서 여러 action들을 의미하는 검정색 도트를 모두 모아 평균을 구했다면, $v_{*}(s)$ 는 검정색 도트 중 최대값을 선택해 계산하는 전략을 취한다. 앞서 예시로 설명했던 그래프에서도 optimal한 값을 위해 둘 중 하나를 골랐는데, 바로 그것을 수식으로 설명한 것이 위의 식이다.

$q_{*}(s,a)$ 는 앞서 설명한 것과 같이 $q_{\pi}(s,a)$ 와 똑같다. 이 말은, action을 취해 발생할 수 있는 모든 상태값 $s'$ 을 아울러 평균을 내서 값을 구하는게 여전히 유효하다는 의미이다.

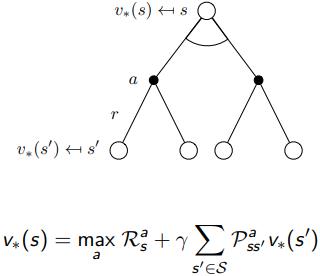
그래서 $v_{*}(s)$ 관점에서의 트리와 $q_{*}(s,a)$ 관점에서의 트리 구조를 각 두단계로부터 합치게 되면, 위와 같이 표현할 수 있다. 흰색 동그라미는 state, 검정색 도트는 action으로써 이해하면 좋다.

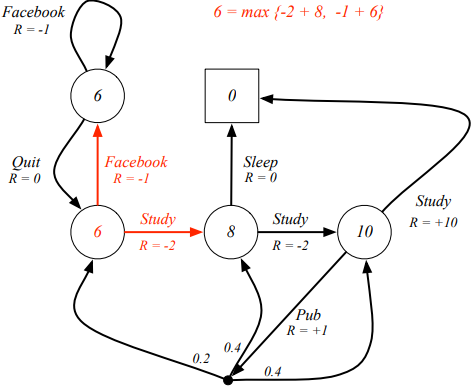
Bellman optimality eqation을 적용하면 위의 그래프와 같이 {Facebook, Study} 중 Study라는 action을 선택하게 된다.

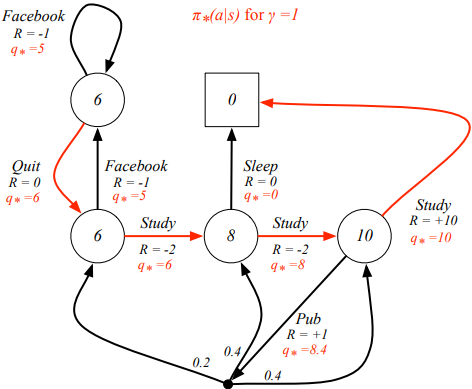
그리고 Optimal policy는 빨간색 화살표대로 정해지게 된다.

Bellman Optimality Eqation을 풀기 위해서는 Value Iteration, Policy Iteration, Q-learning, Sarsa와 같은 non-linear한 알고리즘이 사용된다고 하며(Max를 구하는 부분 덕분에(?)), 이것들은 다음 시간에 배우게 될 것 같다. 기회가 되면 포스팅을 해 봐야 겠다.