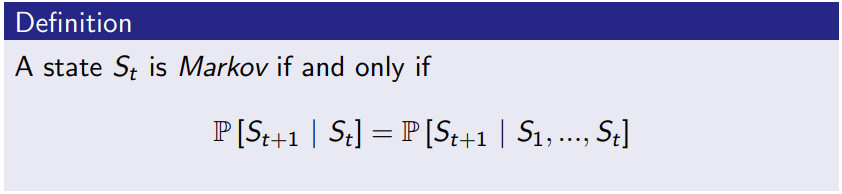
강화학습에 자주 등장하는 개념인 MDP에 대한 깊이 있는 이해를 위해 정리를 해보려고 한다. 출처 자료로 딥마인드의 수석 연구 과학자이자 University College London의 교수를 역임하셨던 David Silver의 Lecture note를 사용하였다.
내용을 이해하기 위해서는 5가지 MDP의 구성요소를 이해하고 넘어가는 것이 좋다.
Definition
- Agent:
앞으로 실험 상황에서 연속된 행동을 하게 될 주체, 대리인
- State():
t 시간에서의 Agent의 상황과 상태
- Action():
State 에서 Agent가 취할 수 있는 행동들
- Reward():
Agent가 움직이면서(= Action 를 진행하면서) 발생하는 보상 점수
- Transition probability(=matrix)():
Agent가 에서 특정 다음 상태인 로 넘어갈 확률을 모아놓은 분포
로 풀어쓸 수 있다. - Discount factor():
Agent가 최단, 최소 경로로 인한 합리적인 보상을 얻게 하기 위하여, 시간에 제약을 두기 위한 factor.
오랜 기간에 걸쳐 목표달성을 하는 것에 대한 패널티를 줌 []
Markov Deicision Processes에서 중요한 4가지 토픽은 다음과 같으며,
이번 시간에는 1) Markov Processes, 2) Markov Reward Processes를 다뤄보도록 하겠다.
1) Markov Processes
2) Markov Reward Processes
3) Markov Decision Processes
4) Extensions to MDPs
Markov Processes

Markov property는 "미래는 현재로부터 영향을 받으며, 이전 과거에 대해서는 독립적이다"는 가정을 가지고 있다.
- 상태() 자체가 과거의 정보를 모두 담고 있다.
- 즉, 상태()는 미래를 위한 충분한 통계량을 지니고 있다.

Markov process(= Markov chain)는 기억이 없는 무작위 프로세스로, Markov property의 과거의 모든 상황을 현재에 녹여냈다는 컨셉을 기반으로 하여 random state들인 , , ... 의 연속적인 상태를 나열한 것이라 할 수 있다.
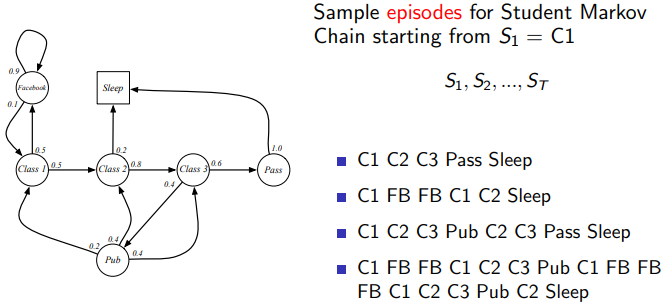
이 그림은 Markov chain을 예시로 하고 있는데, 학생인 Agent에 대해 을 시작으로 여러 에피소드가 발생할 수 있다는 것을 보여준다.
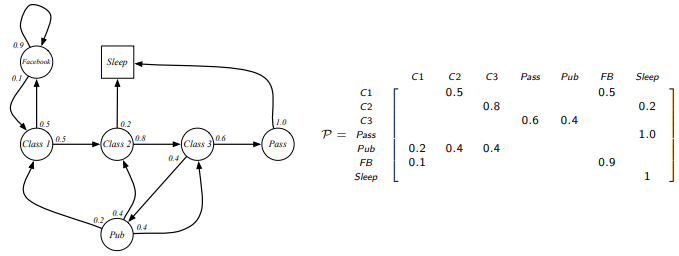
이를 transition matrix로 표현하면, 오른쪽과 같은 행렬로 정리가 되며, 각 -> 별 상태 변환 확률값을 얻을 수 있다.
Markov Reward Processes

Markov Reward Process는 앞선 Markov Process에 가치를 측정하는 reward()와 discount factor()(맨 처음 definition에서 소개)를 더한 개념이다.
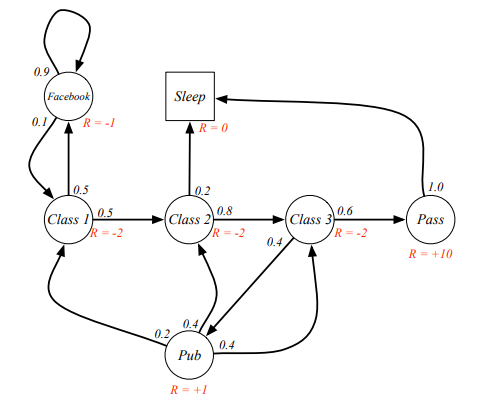
직전의 그림과 다른 점은 각 상태에 대한 reward(R)가 있는 것이다. 예를 들어, Class 1을 지나면 R=-2 의 점수를 획득하고, Pass를 지나면 R=+10 의 점수를 획득한다. 그리고 여기서는 생략되어 있지만, discount factor를 활용하여 다음과 같이 점수를 매긴다.

이 개념을 쉽게 풀어쓰자면, 닥터 스트레인지가 현재 시점 에서 미래를 예측하기 위해 경우의 수를 시뮬레이션 하는 것으로 비유할 수 있을 것 같다. 어떤 시점 를 기준으로 Agent가 그래프를 따라 무작위 이동하는 것을 시뮬레이션 했을 때, 받는 reward를 시간이 지남에 따라() 나열하고, 총 reward를 합하는 그런 모양새인데(), 각 시간이 지나면서 discount factor()를 곱해 시간이 지체되면 패널티를 주겠다는 것을 의미한다.

그래서 state value function 는 특정 시점에서의 상태 를 조건부로, 닥터 스트레인지 시뮬레이션 값()을 모두 계산하여 평균값을 반환하는 함수라고 해석할 수 있다.

위에 설명된 return 를 샘플 에피소드 몇개에 대해 계산해보았을 때의 예시는 위와 같으며, 다양한 에피소드에 따른 다양한 return 결과가 나타나는 것을 확인할 수 있다. 이와 같이 발생가능한 모든 에피소드의 평균값을 구한다면 을 얻을 수 있을 것이다.
Bellman Equation for MRPs
Bellman Equation은 위에 언급한 state value function을 효과적으로 연산할 수 있게 도와주며, dynamic programming 개념을 활용해 문제를 간소화해주는 고마운 알고리즘이다. 실제로 이걸 공부하면서 Deep learning의 Backpropagation을 연상하게 되었는데, 끝에서부터 gradient를 순차적으로 구해서 합치는(곱) 것과 유사하다는 생각이 들었다.

state value function 를 두가지로 쪼갤 수 있는데, 매 순간마다
1) 다음 스텝에서의 reward 와
2) 그 후에 감가상각 되는 state를 로 나타낼 수 있다.
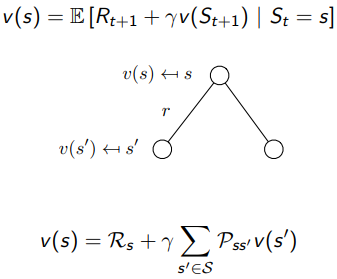
이것을 위 그림의 트리구조를 보면서 생각한다면 다음과 같이 설명할 수 있을 것 같다.
Root node에 존재하는 첫번째 는 모든 다음 state를 선택 할 수 있는데, 첫번째 가지 로 뻗어나갔을 때, 발생하는 reward()와, transition probability(), 새로운 state value function 를 토대로 값을 구해 나가게 된다.
이는 한 스텝 발을 떼고 거기에서의 리워드와 다음 state value를 상정하고, 계속 식을 전개해 나가다가 state value 가 끝지점까지 내려가게 되면 그때부터 트리 가지의 위를 점차 올라가면서 누적값을 토대로 상위 값을 구하는 방식으로 보인다(트리가 아닌 그래프 형태의 cyclic한 상황이 나오는 경우가 있긴 한데 좀 더 알아봐야 할 듯).
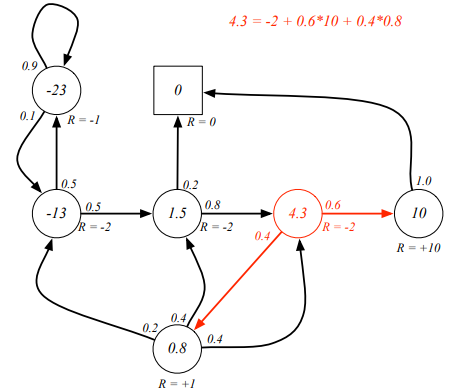
Class 3에서의 Bellman Equation 결과값은 Class 3의 다음 시뮬레이션인 빨간색 화살표 한 스텝에 대한 계산값을 구한 것으로, 이 한스텝의 값들은 이미 그 다음 단계의 모든 에피소드를 포함한 값이라 간편하게 값을 구할 수 있다.

Bellman equation을 간소화 하면, 위 아래와 같이 심플하게 구현될 수 있으며, 작은 규모의 MRPs에서는 linear equation과 같이 연립방정식 식으로 값을 구할 수 있다고 한다.

