Segment Tree

• 여러 개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 구하는 방법
• 데이터의 합을 가장 빠르고 간단하게 구할 수 있는 자료구조

Brute Force

• 단순 배열을 이용해 선형적으로 구하기
• O(n)의 시간복잡도를 가진다

Segment Tree

• 트리 구조의 특성을 이용하여 구하기
• 구간 합을 구할 때O(logN)의 시간복잡도를 가진다
• 최악의 경우 4N 크기의 배열을 가진다
  

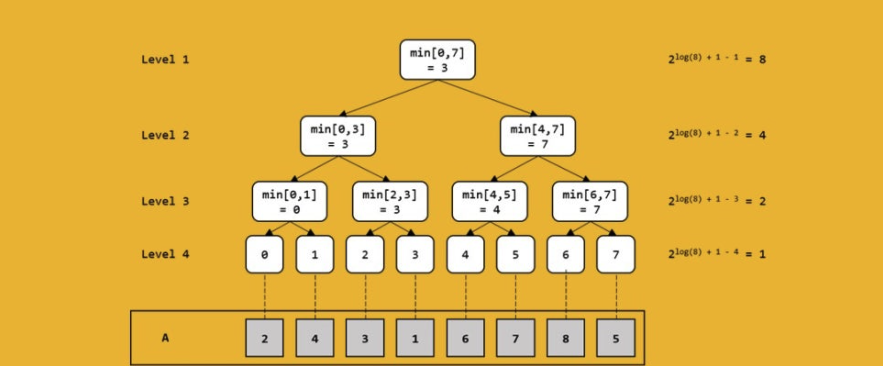
Segment Tree 생성

1. Root Node부터 Leaf Node까지 내려가기
2. Leaf Node에 도착 시, 해당하는 값을 넣고 return
3. Root Node까지 올라가며 Leaf Node가 아닌 Node에는 (Left Node + Right Node)값을 넣고 return

• O(N)의 시간복잡도를 가진다

// start: 시작 인덱스, end: 끝 인덱스
static int init(int start, int end, int node){
	if(start == end) return tree[node] = input[start];
    int mid = (start + end) / 2;
   	// 재귀적으로 두 부분으로 나눈 뒤에 그 합을 자기 자신으로 
    return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}

Segment Tree 수정

1. 수정할 Index에 해당하는 Leaf Node까지 내려가지
2. Root Node까지 올라가며 해당 Index를 포함하고 있는 모든 구간 합 Node들을 갱신

// start: 시작 인덱스, end: 끝 인덱스
// index: 구간 합을 수정하고자 하는 노드
// dif: 수정할 값
static void update(int start, int end, int node, int index, int diff){
	// 범위 밖에 있는 경우
    if(index < start || index > end) return;
    // 범위 안에 있으면 내려가며 다른 노드도 갱신
    tree[node] += diff;
    if(start == end) return;
    int mid = (start + end) / 2;
    update(start, mid, node * 2, index, diff);
    update(mid + 1, end, node * 2 + 1, index , diff);
}

Segment Tree 구간 합 구하기

// start: 시작 인덱스, end: 끝 인덱스
// left, right: 구간 합을 구하고자 하는 범위
static int sum(int start, int end, int node, int left, int right){
	// 범위 밖에 있는 경우
    if(left > end || right < start) return 0;
    // 범위 안에 있는 경우
    if(left <= start && end <= right) return tree[node];
    // 그렇지 않다면 두 부분으로 나누어 합을 구하기
    int mid = (start + end)/2;
    return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}

백준 2042 구간 합 구하기

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

/**
 *  시간 : 496ms, 메모리: 131,684KB
 *  세그먼트트리
 */
public class Main {
    static int N, M, K;
    static long[] tree;
    static long[] input;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        StringBuilder sb = new StringBuilder();
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        K = Integer.parseInt(st.nextToken());
        input = new long[N];
        tree = new long[N*4];
        for (int i = 0; i < N; i++) {
            input[i] = Long.parseLong(br.readLine());
        }
        init(0, N-1, 1);
        for (int i = 0; i < M+K; i++) {
            st = new StringTokenizer(br.readLine());
            int a = Integer.parseInt(st.nextToken());
            if(a == 1){
                int b = Integer.parseInt(st.nextToken());
                long c = Long.parseLong(st.nextToken());
                long diff = c - input[b-1];
                input[b-1] = c;
                update(0, N-1, 1, b-1, diff);
            }else{
                int b = Integer.parseInt(st.nextToken());
                int c = Integer.parseInt(st.nextToken());
                long sum = sum(0, N-1, 1, b-1, c-1);
                sb.append(sum).append("\n");
            }
        }
        System.out.print(sb);
        br.close();
    }
    static long init(int start, int end, int node){
        if(start == end) return tree[node] = input[start];
        int mid = (start + end)/2;
        return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
    }

    static long sum(int start, int end, int node, int left, int right){
        if(left > end || right < start) return 0;
        if(left <= start && end <= right) return tree[node];
        int mid = (start + end)/2;
        return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
    }
    static void update(int start, int end, int node, int index, long diff){
        if(index < start || index > end) return;
        tree[node] += diff;
        if(start == end) return;
        int mid = (start + end)/2;
        update(start, mid, node * 2, index, diff);
        update(mid + 1, end, node * 2 + 1, index , diff);
    }
}