Problem Solving

M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다

문제 > 하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다. 3 : 3 (한 가지) 41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지) 53 : 5+7+11+13+17 = 53 (두

《보드게임컵》을 준비하다 지친 은하는 보드게임컵 참가자들을 경기장에 몰아넣고 결투를 시키는 게임 《수 나누기 게임》을 만들었습니다.《수 나누기 게임》의 규칙은 다음과 같습니다.게임을 시작하기 전 각 플레이어는 $1$부터 $1\\,000\\,000$ 사이의 수가 적힌 서

인체에 치명적인 바이러스를 연구하던 연구소에서 바이러스가 유출되었다. 다행히 바이러스는 아직 퍼지지 않았고, 바이러스의 확산을 막기 위해서 연구소에 벽을 세우려고 한다.연구소는 크기가 N×M인 직사각형으로 나타낼 수 있으며, 직사각형은 1×1 크기의 정사각형으로 나누어

스타트링크에서 판매하는 어린이용 장난감 중에서 가장 인기가 많은 제품은 구슬 탈출이다. 구슬 탈출은 직사각형 보드에 빨간 구슬과 파란 구슬을 하나씩 넣은 다음, 빨간 구슬을 구멍을 통해 빼내는 게임이다.보드의 세로 크기는 N, 가로 크기는 M이고, 편의상 1×1크기의

Java로 코딩테스트를 준비하기 위한 입출력 정리

서로 다른 것들 중 몇 개를 뽑아서 한 줄로 나열하는 것서로 다른 n개 중 r개를 택하는 순열은 아래와 같이 표현한다.순서O, 중복 XnPr그리고 nPr은 다음과 같은 식이 성립한다.nPr = n \* (n-1) \* (n-2) \* … \* (n-r+1)nPn =

서로 다른 n개의 원소 중 r개를 순서 없이 골라낸 것을 조합이라고 부른다.nCr = nCn-rnCr = n!/(n-r)!\*r!nCr = n-1Cr-1 + n-1Cr서로 다른 n개의 원소 중에서 중복을 허락하여 r개를 순서 없이 골라낸 것을 중복 조합이라고 부른다.n

집합에 포함된 원소들을 선택하는 것이다.N개 원소로 이루어진 집합에서 nC1, nC2, nC3, nC4, … , nCn-1, nCn ⇒ power set다수의 중요 알고리즘들이 원소들의 그룹에서 최적의 부분 집합을 찾는 것이다.ex) 배낭 짐싸기(knapsack)집합의

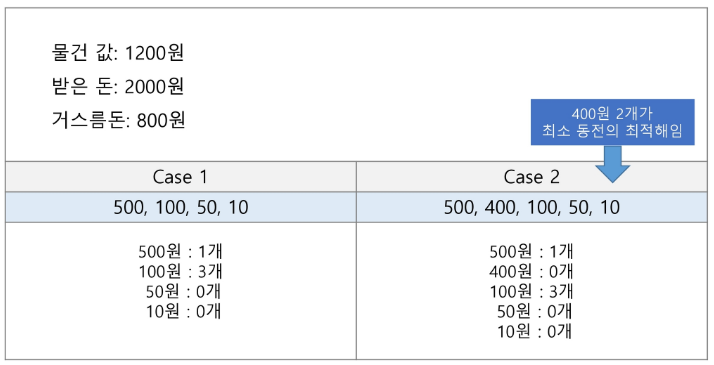
탐욕 알고리즘은 최적 해를 구하는 데 사용되는 근시안적인 방법최적화 문제(optimization)란 가능한 해들 중에서 가장 좋은(최대 또는 최소) 해를 찾는 문제이다.일반적으로, 머리 속에 떠오르는 생각을 검증 없이 바로 구현하면 Greedy 접근이 된다.여러 경우

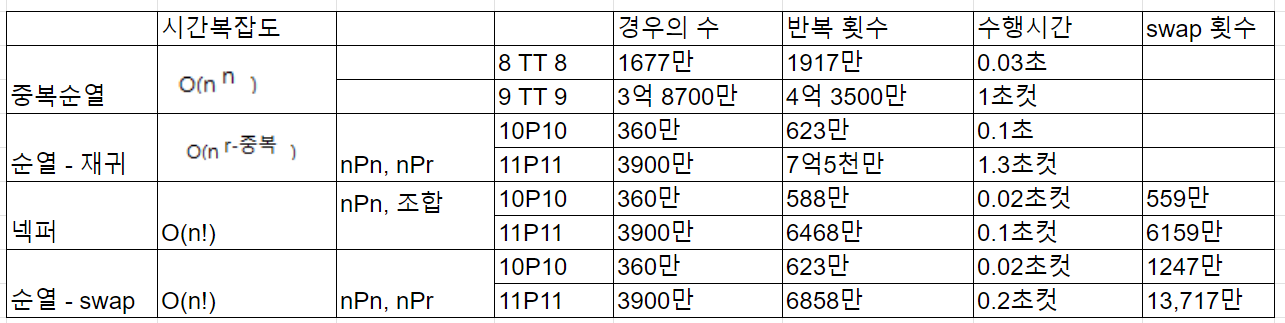
현 순열에서 사전 순으로 다음 순열 생성배열을 오름차순으로 정렬한 후 시작한다.아래 과정을 반복하여 사전 순으로 다음으로 큰 순열 생성(가장 큰 내림차순 순열을 만들 때까지 반복한다.)뒤쪽부터 탐색하며 교환 위치(i - 1)찾기 (i : 꼭대기)뒤쪽부터 탐색하며 교환

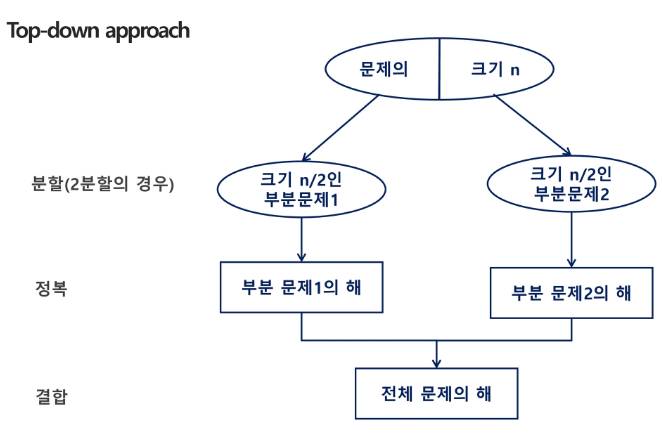
1805년 12월 2일 아우스터리츠 전투에서 나폴레옹이 사용한 전략전략이 우세한 연합군을 공격하기 위해 나폴레옹은 연합군의 중앙부로 쳐들어가 연합군을 둘로 나눔둘로 나뉜 연합군을 한 부분씩 격파함분할(Divide) : 해결할 문제를 여러 개의 작은 부분으로 나눈다.정복

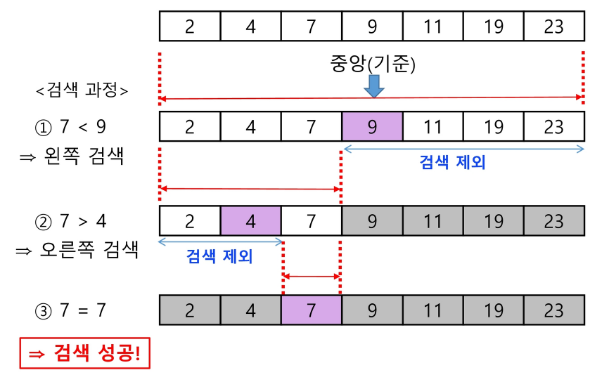
자료의 가운데에 있는 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법목적 키를 찾을 때까지 이진 탐색을 순환적으로 반복 수행함으로써 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행함 이진 검색을 하기 위해서는 자료가 정렬된 상태

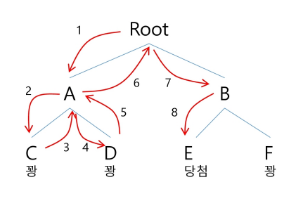
퇴각 검색모든 조합을 시도해서 문제의 해를 찾는다.해를 얻을 때까지 모든 가능성을 시도한다.모든 가능성은 하나의 트리처럼 구성할 수 있으며, 가지(선택지) 중에 해결책이 있다.여러 가지(선택지)들이 존재하는 상황에서 하나의 가지를 선택한다.선택이 이루어지면 새로운 선택

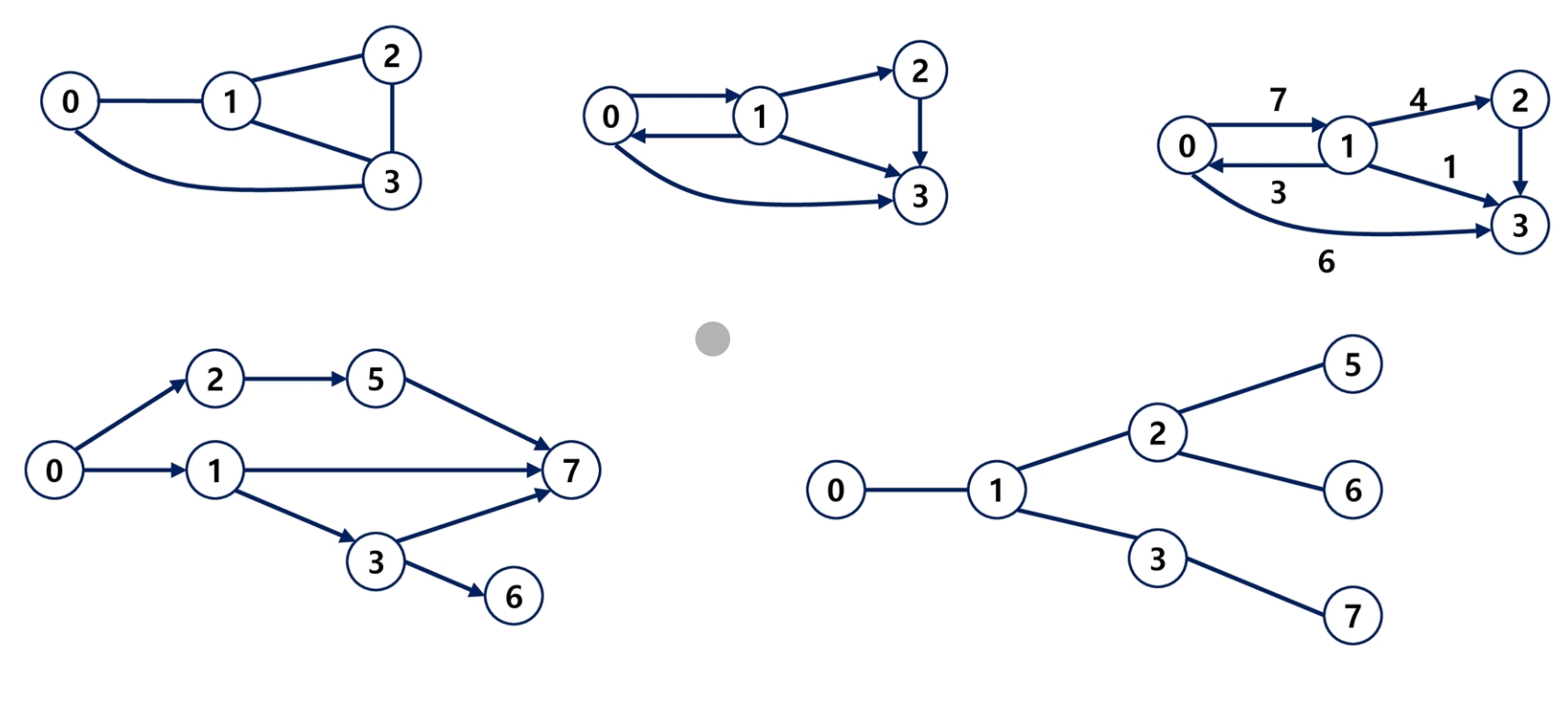
그래프는 아이템(사물 또는 추상적 개념)들과 이들 사이의 연결 관계를 표현한다.정점(Vertex) : 그래프의 구성요소르 하나의 연결점간선(Edge) : 두 정점을 연결하는 선차수(Degree) : 정점에 연결된 간선의 수그래프는 정점(Vertex)들의 집합과 이들을

너비우선탐색은 탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문한 후에, 방문했던 정점을 시작으로 하여 다시 인접한 정점들을 차례로 방문하는 방식인접한 정점들에 대해 탐색을 한 후, 차례로 다시 너비우선탐색을 진행 하므로, 선입선출 형태의 자료구조인 큐를 활용함.가

시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회 방법가장 마지막에 만났던

방향 그래프의 정점들을 변의 방향을 거스르지 않도록 나열하는 것을 의미한다.위상 정렬은 순서가 정해져 있는 작업들을 차례대로 수행해야 할 때, 그 순서를 결정해 주는 알고리즘이다.위상 정렬을 가장 잘 설명해 줄 수 있는 예로 교육과정의 선수과목(prerequisite)

\- 그래프에서 최소 비용 문제 1\. 모든 정점을 연결하는 간선들의 가중치의 합이 최소가 되는 트리 2\. 두 정점 사이의 최소 비용의 경로 찾기\- 신장 트리 \- n개의 정점으로 이루어진 무방향 그래프에서 n개의 정점과 n-1개의 간선으로 이루어진 트리\-

시작정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘시작 정점에서의 거리가 최소인 정점을 선택해 나가면서 최단 경로를 구하는 방식이다.탐욕 기법을 사용한 알고리즘으로 MST의 프림 알고리즘과 유사하다.우선순위큐에 PQ에 있는 정점에서 해당정점까지의 거리가 가장

큰 문제에 대한 답을 얻기 위해 동일한 문제이지만 크기가 더 작은 문제들을 먼저 해결한 뒤, 그 결과들을 이용해 큰 문제를 비교적 간단하게 해결하는 기법제귀 함수 호출시 중복으로 호출하는 부분을 줄이고자 결과값을 기록하고, 그 기록한 값을 참조하는 것높은 수에서 낮은

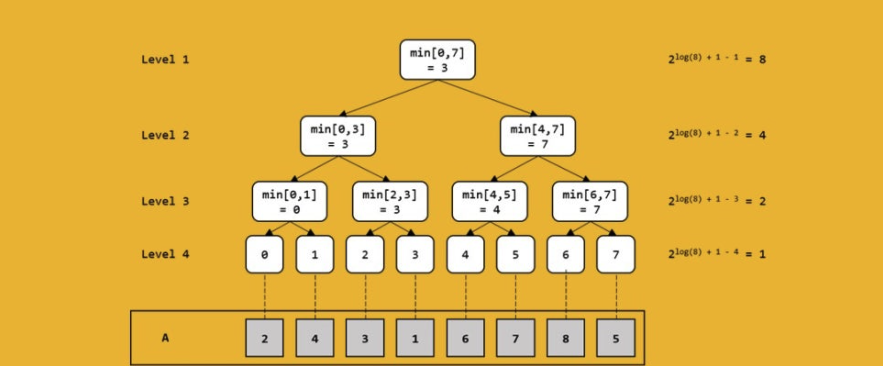
여러 개의 데티어가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 구하는 방법데이터의 합을 가장 빠르고 간단하게 구할 수 있는 자료구조단순 배열을 이용해 선형적으로 구하기O(n)의 시간복잡도를 가진다트리 구조의 특성을 이용하여 구하기O(logN)의 시간복잡도를 가진

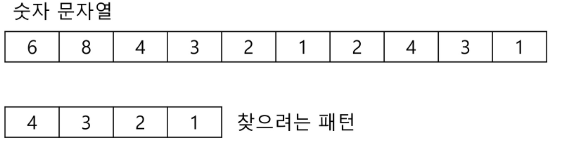
문자열 검색을 위해 해시 값 함수를 이용패턴 내의 문자들을 일일이 비교하는 대신에 패턴의 해시 값과 본문 안에 있는 하위 문자열의 해시값만을 비교최악의 시간 복잡도는 $O(MN)$이지만 평균적으로는 선형에 가까운 빠른 속도를 가지는 알고리즘문자열 대신 숫자로 생각해 보

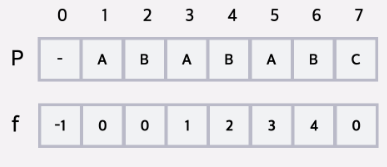
Rabin Karp 알고리즘을 이용하면 길이가 각각 n, m인 두 문자열 T(=text), P(=pattern)가 주어졌을 때 문자열 T의 부분 문자열 중 문자열 P와 일치하는 경우가 있는지를 O(N+M)에 구할 수 있다고 했습니다. 이렇게 부분 문자열로서 어디에서 일

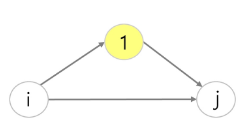
한 도시에서 다른 도시로 가장 빨리 갈 수 있는 경로를 찾는 문제가중치 포함, 방향성 그래프에서 최단경로 찾기최적화 문제(optimization problem)주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때, 이 가운데에서 가장 최적인 해답(optimal so

최장 증가 부분 수열어떤 수열이 왼쪽에서 오른쪽으로 나열되어 있으면, 그 배열 순서를 유지하면서 크기가 점진적으로 커지는 가장 긴 부분 수열을 추출하는 문제수열의 모든 부분 집합을 구하여 그 부분 집합이 증가 수열인지 판별한다증가 수열 중 가장 길이가 긴 값을 구한다e

$S = {item_1, item_2, ..., item_n}$, 물건들의 집합$w_i : item_i 의 무게, P_i = item_i의 값$W = 배낭이 수용 가능한 총 무게문제 정의배낭에 물건을 통째로 담아야 하는 문제물건을 쪼갤 수 없는 경우완전 탐색으로 물건들

최하위 노드, (idx & -idx)를 빼가며 갱신하고 업데이트하는 간단한 트리, Binary Indexed Tree라고도 함세그먼트 트리의 특징이 담김세그먼트 트리와는 다르게 모든 세그먼트를 만들 필요가 없음idx = (S & -S)10010에서 최하위 켜져있는 비트

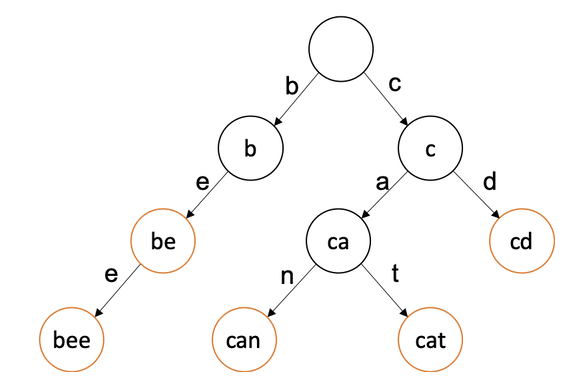
Trie: 트라이(Trie)란 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조트리의 루트에서부터 자식들을 따라가면서 생성된 문자열들이 트라이 자료구조에 저장되어 있다고 볼 수 있다저장된 단어는 끝을 표시하는 변수를 추가해서 저장된 단어의 끝을 구분할 수