Background

• SQL $\rarr$ practical lang, procedual lang, declarative lang
• Relational Lang $\rarr$ theoretical lang
• Relational Calculus $\rarr$ 서술어들의 결합을 활용하여 원하는 조건을 명시
• Tuple Calculus $\rarr$ Tuple(row) 기반 해석(SQL의 이론적 해석)
• Domain Calculus $\rarr$ Column 기반 해석

Relational Algebra

Relational Algebra ?

• 관계 대수, relation들에 대한 연산을 정의한 set
• 기본적 검색 요청문 또는 queries를 사용자가 기술할 수 있도록 한다.

operation의 결과 : new relation

• relation간의 연산의 결과로 relation이 도출 -> "system이 닫혀있음"
  • 관계 대수의 대상이 relation이고, 연산의 결과도 relation이므로 관계 대수는 relations에서만 적용된다.

관계 대수 operations의 일련의 과정은 relational algebra expression을 형성

• relational algebra expression의 결과 database query의 result를 나타내는 relation이다.

relational algebra가 중요한 이유 ?
1) relational model operations를 위한 formal foundation을 제공 (수학적인 notation을 활용, 정형화된 기초 제공)
2) RDBMS에서 필수적인 부분인 query processing & optimization modules에서 queries를 구현하고 최적화하는데 기초로서 사용된다. (효율성 측면)
3) 일부 개념은 RDBMS용 SQL 표준 query 언어에 통합되었다. (정확도 측면)

classic operations의 2 groups
G1) 수학적 set theory로부터의 set operations를 포함

• formal relational model에서 각 relation은 tuples의 set이다.
• Ex) $UNION$($\cup$), $INTERSECTION$($\cap$), $SET\space DIFFERENCE$($-$), $CROSS$ ($CARTESIAN$) $PRODUCT$(x)

G2) relational databases에 대한 operations로 구성

• Unary operations (단일): $SELECT$(symbol: $\sigma$ (sigma)), $PROJECT$(symbol: $\pi$ (pi)), $RENAME$(symbol: $\rho$ (rho))
• Binary operations (2개): $JOIN$ and $DIVISION$

Relational Calculus

relational queries를 기술하는데 고수준의 declarative language 제공

relation algebra와의 주된 차이점

• relational algebra는 연산의 순서를 결정할 수 있다. (절차적)
• relational calculus는 연산의 순서는 결정할 수 없고, 원하는 연산만을 정의

Two variations :
확인할 결과를 위한 조건 적시에 따라 구분된다.
1) tuple relational calculus: tuples 단위로의 변수 사용 (rows)
2) domain relational calculus: attributes의 domains(values) 단위로의 변수 사용 (columns)

UNARY RELATIONAL OPERATIONS

Recall: the COMPANY Database

One Possible DB State for COMPANY

Unary Relational Operation: SELECT (1/4)

• $\sigma$ (sigma)로 표기
• selection condition을 기반으로 relation으로부터 tuples의 subset을 선택하기 위해 사용한다.
  • selection condition -> "filter" 역할
  • 조건을 충족하는 tuples만 남게되고 나머지 tuples은 filtered out
• Ex) "Selects the EMPLOYEE tuples whose department number is 4.”
  전체 table 중 "EMPLOYEE"에서 "Dno=4"인 것만 select
  ( ) : 연산의 우선순위 의미

Unary Relational Operation: SELECT (2/4)

일반적인 select operation 표기법

• symbol $\sigma$는 "select(ion) operator"를 의미 (SQL문의 select와 다른 개념)
• selection condition은 Boolean expression
  • $<selection \space condition>$은 $<attribute \space name>$, $<comparizon \space op>$, $<constant \space value>$ 형태를 갖춘 여러 개의 절로 구성된다.
    • 차례대로 $R$(=relation)의 attribute name, 비교 연산자, attribute domain으로부터의 constant value를 의미
  • 그리고 이러한 절들은 $and$, $or$, and $not$으로 연결될 수 있다.
• selection condition을 true로 만드는 tuples는 선택되어 select operation의 result에 나타나고, 반대로 false로 만드는 tuples는 result에 나타나지 않는다.

Unary Relational Operation: SELECT (3/4)

Several properties:

1) SELECT operation은 input relation $R$과 동일한 schema를 가지는 relation $S$를 만들어낸다. 즉 Schema의 변경이 없다.
2) $\sigma$는 commutative하다.

3) 2)에서 다룬 commutative한 특성때문에, 순서에 따른 결과의 차이가 없다.

4) 여러 개의 $\sigma$ operation은 단일 $\sigma$ operation으로 변환될 수 있다.

• 총 n개의 condition의 경우, $R$을 n번 확인해야 하기에 "비효율적"일 수 있다.

5) result tuples의 수는 input relation $R$의 tuples 수보다 클 수 없다. (작거나 같다.) 그리고 $|\sigma_c(R)| \leq |R|$과 같이 표기한다.

• 하지만 $\sigma$로부터 얻은 relation의 attributes의 수는 input relation $R$의 degree와 동일하다.

6) Unary하다. 즉, 단일 relation의 각각의 tuple에 적용된다.

Unary Relational Operation: SELECT (4/4)

Ex) $\sigma_{(Dno=4\space AND\space Salary>25000)OR(Dno=5\space AND\space Salary>30000)}(EMPLOYEE)$

• (In relation algebra) $\sigma_{(Dno=4\space AND\space Salary>25000)}(EMPLOYEE)$
• (In SQL query)
  $\sigma$ => 일반적으로 WHERE 절에 기술된다.

Unary Relational Operation: PROJECT (1/3)

• $\pi$(pi)로 표기
• table로부터 특정 columns만 선택하고, 나머지는 버린다.
  • 이러한 연산은 relation을 두 개의 relation으로 vertical partition하는 결과;
    하나는 필요한 relation, 나머지는 필요하지 않은 relation

SELECT와의 차이점: select는 filtering의 단위가 tuples, PROJECT는 attributes(columns)

• Ex) EMPLOYEE의 last name, first name, and salary를 list하기 위해서는 다음과 같이 기술할 수 있다.
  $\pi_{LNAME,FNAME,SALARY}(EMPLOYEE)$
  

Unary Relational Operation: PROJECT (2/3)

일반적인 project operation 표기법

• symbol $\pi$는 "project operator"를 의미
• $<attribute \space list>$: relation $R$(또는 query의 result)로부터 얻고 싶은 attributes의 list
  • $R$은 relational algebra expression이고, result 또한 relation이다.
• $\pi$는 모든 tuple 중복을 제거한다.
  • formal relation model에서, $\pi$의 result는 tuples의 set이어야 한다.
    • 수학적으로 set은 중복된 요소를 가질 수가 없다.
  • 이러한 점이 practical model과 다른 점인데, SQL을 예로 들면 어떤 점이 다른가 ?
    • SQL은 어떠한 중복도 제거하지 않는다. (중복 제거의 높은 비용때문에)

Unary Relational Operation: PROJECT (3/3)

Several properties:

1) $\pi_{<attribute \space list>}(R)$의 result tuple의 수는 $|R|$ 보다 작거나 같다.

• 중복이 있는 경우, $\lt|R|$
• attribute list가 $R$의 key를 포함하고 있는 경우(=중복이 있을 수 없는 경우), $\pi_{<attribute \space list>}(R)$의 result의 degree $= |R|$

2) $\pi$는 NOT commutative

• Ex) attr. list1 = {Dno, Salary}, attr. list2= {Dno}:
  $\pi_{<attr.list1>}(\pi_{<attr.list2>}(R)) \neq \pi_{<attr.list2>}(\pi_{<attr.list1>}(R))$
• 가장 왼쪽에 있는 attribute list가 $\pi$의 result를 결정
• Ex) $<attribute \space list2> \supseteq <attribute \space list1>$ (ex.{Sex, Salary} $\supseteq$ {Salary})인 경우, $\pi_{<attr.list1>}(\pi_{<attr.list2>}(R)) = \pi_{<attr.list1>}(R)$
  • attr.list1은 무조건 result에 포함되어야 한다. => Commutative할 수가 없다.

Ex): $\pi_{Sex, Salary}(EMPLOYEE)$

Applying Sequences of Operations: Single Expression vs. Sequence of Operations

relational algebra operations를 여러 개 적용할 수 있다.
1) in-line expression : operations를 중첩하고 single relational algebra expression처럼 write

2) assignment operation 사용 : 중간과정에 있는 relation마다 name을 부여하고, assignment symbol($\larr$)을 사용해서 operation의 중간 결과를 명시적으로 확인
RESULT는 DEPT5_EMPS와 동일한 attribute names를 가질 것이다.

Unary Relational Operations: RENAME

• $\rho$(rho)로 표기
• relation의 attributes를 renaming하거나, relation name을 renaming하기 위해 사용하고, 특히 JOIN을 포함한 complex queries에서 유용하다.
• Expression:
  • $\rho_{B_1,B_2,...,B_n}(R)$ : $B_1, B_2,...,B_n$으로 attribute names만 변경 (이때, attribute의 순서 중요)
  • $\rho_S(R)$ : relation name만 $S$로 변경
  • $\rho_{S(B_1,B_2,...,B_n)}(R)$ : relation name과 attribute names 모두 변경

RELATIONAL ALGEBRA OPERATIONS FROM SET THEORY

UNION

• $\cup$으로 표기
• Binary operation
  • 중복은 제거된다.
  • 피연산자 relations는 서로 "type compatible"해야 한다.
    • 이러한 특징은 다른 set operators에도 적용된다.
• Ex) “Retrieve the SSNs of all employees whose either Work in dept. #5 or Directly supervise an employee who works in dept. #5.”
  UNION의 type-compatible 특징 충족을 위해 renaming 수행
  (Set operation은 type-compatible을 충족해야 가능)

INTERSECTION

• $\cap$으로 표기
• Binary operation
  • 또한 type-compatibility가 전제

SET DIFFERENCE

• $-$으로 표기
• Binary operation
  • $R-S$의 result: $R$에는 존재하지만 $S$에는 존재하지 않는 모든 tuples를 포함하는 relation
    • $R$과 $S$는 type-compatibility를 만족해야 한다.
• Not Commutative
  

Example to Illustrate the Result of UNION, INTERSECT, and DIFFERENCE

Some Prosperities of Set Operations

• UNION & INTERSECTION은 Commutative
  • 즉, 교환법칙이 성립
• UNION & INTERSECTION은 associative operations
  • 연산의 순서가 중요하지 않다.
• DIFFERENCE는 not commutative
  • $(R-S) \neq (S-R)$

CARTESIAN (or CROSS) PRODUCT

• 조합 방식으로 두 relations의 tuples를 결합할 때 사용한다.
• $R(A_1, A_2, ..., A_n)\times S(B_1, B_2, ..., B_m)$와 같이 표기
  • $R$과 $S$의 모든 tuple을 결합
  • $R$ and $S$는 type-compatible할 필요는 없다.
• Result: $Q(A_1, A_2, ..., A_n, B_1,B_2, ..., B_m)$
  • relation $Q$의 degree : n + m (attributes)
  • $Q$의 cardinaliy (tuples의 수) : $|R| \times |S|$
• 해당 operation의 대다수의 경우는 meaningless and expensive

CARTESIAN PRODUCT: Example

“Retrieve a list of names of each female employee’s dependents.”

CARTESIAN PRODUCT를 수행하여 의미없는 tuple이 존재할 수 있다.아래의 연산과 동일하다.Join은 Complete set에는 포함되지 않는데, 이는 다른 연산으로 구현이 가능하기 때문이다.

BINARY RELATIONAL OPERATIONS

JOIN

• Binary operations; $⋈$로 표기
  • Cartesian과 다른 점 : "Condition"이 추가됨
• relations간의 relationship을 처리할 수 있다는 관점에서 매우 중요
• Ex) “Retrieve the name of the manager of each department.”

  Mgr_ssn=Ssn $\rarr$ EQUIJOIN ($\theta$-join)

JOIN: Some Properties

• 주어진 $R(A_1, A_2, ..., A_n)$ and $S(B_1,B_2,...,B_m)$ relations에 대해서, JOIN operation의 형태는 $R⋈_{<join\space condition>}S$.
  • condition을 true로 만드는 tuple들의 조합이 result
  • Result: $Q(A_1, A_2, ... , A_n, B_1, B_2, ... ,B_m)$
    • relation $Q$의 degree : n + m (attributes) => 결과가 존재하는 경우
      • $r[A_i]=s[B_j]$를 만족하는 $R$의 one tuple과 $S$의 one tuple들이 모인 combination 중 1개의 tuple이 $Q$의 state
  • $Q$의 cardinaltiy $\leq (|R|\times|S|)$
    • $|Q| = |R| \times |S|$ -> join condition이 모든 tuple에 대해 true => "Cartesian product"
      • $|Q| \lt |R| \times |S|$ -> join에 참여하지 않는 tuples out
• 일반적인 JOIN operation이 경우는 Theta-join이라고 하고, $\theta$가 join condition인 경우,
  $R⋈_\theta S$로 표기한다.
• 하나 이상의 대등 조건을 포함하는 join condtions을 EQUIJOIN이라고 한다.
  

Variations of JOIN: EQUIJOIN

EQUIJOIN operation

• join의 가장 흔한 사용
• 대등 비교만을 기술한 join condtions
• EQUIJOIN의 result는 모든 tuples에서 동일한 값을 가지는 attribute의 쌍을 하나 이상 가진다.
  • 하지만, attributes의 names는 동일하면 안된다. (이름까지 동일한 경우 -> NATURAL JOIN)

Variations of JOIN: NATURAL JOIN

• $\star$로 표기
• EQUIJOIN condtion의 두 번째 attribute를 제거하기 위해 사용한다.
  • 동일한 값을 가진 각 attribute 쌍 중 하나는 불필요하다.
• 두 join attribute는 두 relations에서 동일한 이름을 가져야 한다.
  • 그렇지 않다면, natural join 전에 먼저 renaming

Join Selectivity

Join 선택도

• 각 join condition의 특성으로, join 후 선택된 tuple의 비율 (낮을 수록 result의 size $\darr$) => query performance를 결정(commutative)
• $\frac{|Q|}{|R|\times|S|}$로 계산하고, percentage로 표현
  • Cartesian의 경우, join selectivity = 1
• 낮은 selectivity 값은 낮은 result size를 의미하고, I/O를 감소시킴으로써, query 최적화의 성능이 향상된다.
  • highly selective join condition이 더 적은 related tuples을 생성하고, I/O를 더 많이 감소시켜준다.

Inner Joins, n-way Joins, Implementation

Inner joins

• 일종의 "match-and-combine" operation
• CROSS PRODUCT & SELECTION의 combination으로 정의

n-way joins

• multiple tables를 포함하는 join
  

Implementation in SQL:

$<join \space conditon>$ in WHERE, nested relation via IN

Complete Set of Relational Operations

Complete Set

: relational algebra operations의 set {$\sigma$, $\pi$, $\cup$, $-$, $\rho$, $\times$}, 이들만으로 나머지 모든 relational algebra operations를 구현 가능하다.

• Ex)

DIVISION (1/4): Illustration of $T(Y) = R(Z)\div S(X)$

$S$ relation의 $X$ attribute의 $A$의 모든 값을 가지는 $R$ relation의 $Z$ attribute의 $B$의 모든 값을 list

• X = {A}, Y = {B}, and Z = {A,B}
• R의 B의 b2는 a2 값을 가지고 있지 않고, b3는 a1 값을 가지고 있지 않다.

DIVISION (2/4)

• $\div$로 표기
• 분모 relation $S$의 tuples는 relation $S$에 존재하는 모든 값과 일치하는 result ($R$의 subset)에서 해당 tuple을 선택함으로써 분자 relation $R$를 제한한다.

DIVISION (3/4): Example

• “Retrieve the names of employees who work on all the projects that ‘John Smith’ works on.SSN_PNOS : 원하는 tuple을 찾고자 하는 input relation
  SMITH_PNOS : Pno 를 1과 2만 가지고 있음

DIVISION (4/4): Properties

• $\div$는 $\pi$, $\times$, $-$로 표현될 수 있기에 Complete set에 포함되지 않는다.
• universal quantification 또는 모든 condition을 포함하는 query를 처리하기 위한 편의를 위해 정의된다.
  • SQL에서는 이를 위한 statement는 없지만, NOT EXISTS 로 구현 가능하다.

EXAMPLES OF QUEIRES IN RELATIONAL ALGEBRA

Examples in Procedural Form

• Q1: Retrieve the name and address of all employees who work for the ‘Research’ department.
  
• Q6: Retrieve the names of employees who have no dependents.
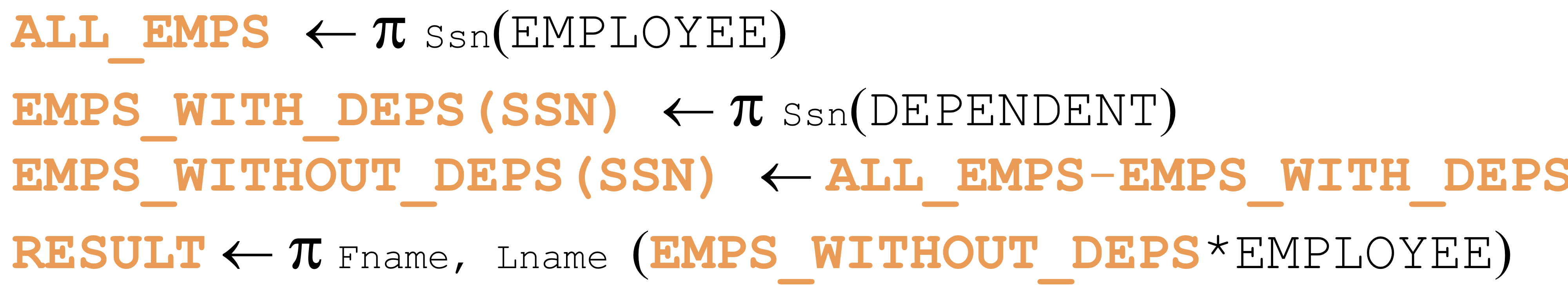  $\pi_{Essn}(DEPENDENT)$가 되어야 하지 않나 ...? (renaming 하기 위해서)
• Q3: Find the names of employees who work on all the projects controlled by department number 5.
  

Examples in Single Expressions

• Q1: Retrieve the name and address of all employees who work for the ‘Research’ department.
  
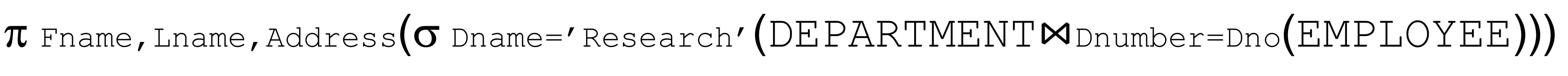
• Q6: Retrieve the names of employees who have no dependents.
  

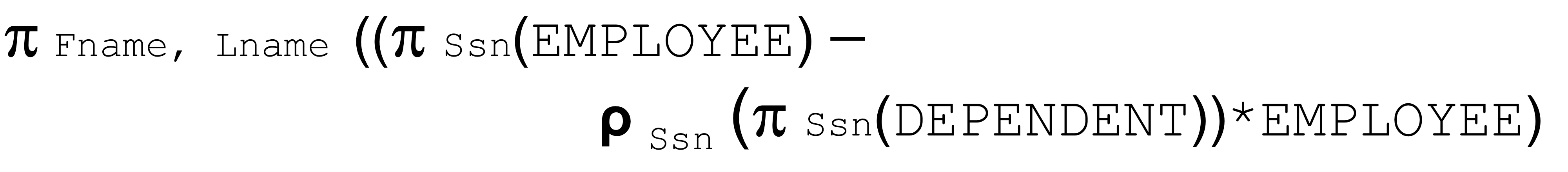
RELATIONAL CALCULUS - THE TUPLE RELATIONAL CALCULUS

Relational Calculus (1/3)

• relational model을 위한 formal language
• 범위 변수로 지정된 새로운 relation을 생성한다.
  • 저장된 relations의 ROWS : "tuple calculus"
  • 저장된 relations의 COLUMNS : "domain calculus"
• calculus expression은 어떻게 query result를 가져올 지에 대한 기술은 하지 않고, 어떤 정보를 result에 포함해야 하는지만을 기술한다. (SQL과 동일한 점이자, relation algebra와 다른 점)
  • relational operations의 순서가 없다.

Relational Calculus (2/3)

• Relational calculus는 nonprocedural(비절차적) or declarative(선언적) language로 간주된다.

Relational Calculus (3/3)

• relation algebra & relation calculus 모두 query language로서 동일한 expressive power를 가진다.
  • 이로 인해 relationally complete language의 개념을 이끌어냈다.
    • relational language $L$에 있는 어떠한 query를 relational calculus로 표현할 수 있다면, $L$을 relationally complete하다고 한다.
  • 대부분의 relational query languages는 relationally complete하다.
    • SQL은 relational calculus나 relatoinal algebra보다 더 강력한 expressive power를 가진다.
      • 가장 큰 표현력을 가졌기 때문에 relationally complete하지 않고,
        SQL의 일부 -> relationally complete

relational calculus가 중요한 이유 ?
1) 확고한 수학적 논리를 가지고 있다: 일반화의 용이
2) RDBMSs를 위한 SQL은 tuple relational calculus에 기초를 두고 있다.

Tuple Relational Calculus (1/3)

• 여러 "tuple variables" 지정을 기반으로 한다.
• 간단한 tuple relational calculus query의 형태:
  $\{t|COND(t)\}$
  $t$: tuple variable, $CONT(t)$: $t$를 포함하는 conditional expression
• result: $COND(t)$를 만족하는 모든 tuples의 set

Tuple Relational Calculus (2/3)

• “Find all employees whose salary is above $50,000.”
  EMPLOYEE(t)는 tuple variable "t"의 범위 relation이 EMPLOYEE임을 지정한다.
  위의 relational calculus query는 아래에 있는 relational algebra query를 변환한 것이다.

Tuple Relational Calculus (3/3)

• A formula (Boolean conditions)
  • logical operators($AND, OR, NOT$)를 통해 하나 이상의 atoms로 구성된다.
  • 규칙 1과 2를 재귀적으로 정의: 해당 규칙을 충족하게 되면, COND로서 사용
    1) 모든 atom은 formula이다.
    2) $F_1$과 $F_2$가 formula이면, $(F_1 AND F_2)$, $(F_1 OR F_2)$, $NOT(F_1)$, and $NOT(F_2)$ 또한 formula이다.